| |
Les simulacions com a recurs didàctic |
| |
|
| |
A la primera pràctica d'aquest mòdul es donen a conèixer possibilitats
diverses de fer simulacions amb ordinador per a una aproximació didàctica
a la llei empírica de l'atzar i el concepte de probabilitat d'un esdeveniment.
|
| |
 Les simulacions amb ordinador ajuden a entendre els conceptes Les simulacions amb ordinador ajuden a entendre els conceptes |
| |
Els aspectes que es tractaran són aquests:
- Idees per a la realització personal de simulacions amb l'Excel.
- Presentació d'una aplicació ja elaborada amb tots els recursos del programa Excel.
- Enllaç a unes MUD del projecte interm@tes
(al portal edu365.com).
|
 |
Comencem a fer simulacions amb l'Excel |
| |
|
| |
Per començar a fer simulacions, convé comentar que l'Excel incorpora
una funció ALEATORIO que permet assignar valors aleatòriament a
una o més cel·les, però si es fa servir aquesta funció, cada vegada que
es recalcula canvien els valors aleatoris i aquest fet fa difícil seguir
una construcció pas per pas. Per aquesta raó, s'aconsella, a l'hora de
fer simulacions, l'opció Herramientas | Análisis de datos | Generación
de números aleatorios.
Tot seguit s'explica una manera de generar el gràfic que fa visual la
llei empírica de l'atzar per al nombre de 6 observats quan es tira successivament
un dau i s'aprofita per comentar altres aspectes. Llavors un dels exercicis
que haureu d'enviar serà anàleg a aquest.
|
|
Ja tenim totes
les dades d'una simulació de 100 tirades d'un dau. Podeu comprovar que si
torneu a executar el procediment ... | Generación de números aleatorios
sense canviar cap de les dades, es fa una altra simulació i s'actualitzen
les taules de freqüències.
Tot seguit s'explica com es pot fer el gràfic que mostra l'evolució
de la freqüència relativa i permet constatar que a mesura que augmenta
el nombre de tirades, la freqüència relativa s'estabilitza al voltant
d'un nombre fix, 1/6 en aquest cas.
La representació que fareu serà la d'una funció empírica: a l'eix
de les x els nombres de tirades; a l'eix de les y les freqüències
relatives. El gràfic més adequat és el següent:
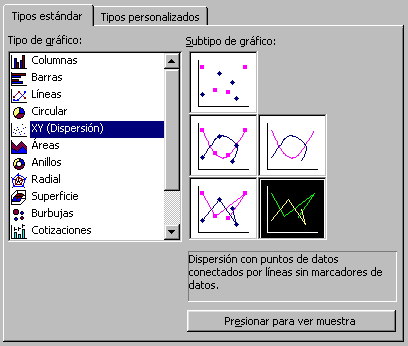
- Abans d'ordenar el gràfic, heu de seleccionar les dues columnes que
tenen els valors de les variables indicades. Seleccioneu la columna
D fent clic a la lletra D, premeu la tecla Control i feu clic
a F. Així seleccionareu també la columna F.
- Activeu l'opció de gràfics i trieu el gràfic Dispersión indicat anteriorment.
- Cliqueu a Finalizar i a partir d'aquest moment podeu fer totes les millores al gràfic que cregueu convenients fins que mostri clarament el que volíem.
|
|
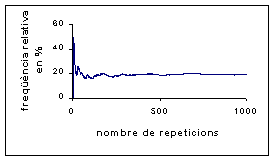
Un gràfic per visualitzar la llei empírica de l'atzar
|
|
|
Coneguem altres recursos didàctics |
| |
|
| |
A l'apartat anterior heu elaborat una simulació amb l'Excel que permet
fer visual la llei empírica de l'atzar i, com a empírica que és, aquest
és sens dubte el millor camí per copsar-ne el significat.
Sens dubte, el fet de fer la pràctica pas a pas facilita la seva inclusió
com a element didàctic en una classe de l'educació secundària. Tanmateix,
és bo de conèixer altres possibilitats molt més elaborades que avancen
en la mateixa línia.
Tot seguit us proposem que reviseu tres MUD que podeu trobar al portal
edu365.com en el marc del projecte interm@tes que entenem
que són excel·lents recursos per a l'ús en una classe, ja sigui a l'aula
d'informàtica com a treball personal, ja sigui amb un projector a manera
de pissarra electrònica.
Accediu, doncs, a l'àrea de matemàtiques
de l'ESO de l'edu, cliqueu a la icona d'interm@tes i,
tot seguit, al botó que porta a la prestatgeria amb l'índex de les miniunitats
didàctiques.
- La primera proposta que us fem és la MUD Comptem boles. A la
portada veureu que hi ha un enllaç que permet estudiar el funcionament
de la miniaplicació (applet). Comenceu per aquí.
- A la mateixa portada trobareu un altre enllaç que porta al començament
de l'activitat. Si hi feu clic, trobareu unes indicacions detallades
d'exemples suggerits. Veureu de seguida que si feu la pràctica amb
alumnes se'ls fa molt entenedor:
- El fet que la influència de l'atzar no ens permet mai assegurar
res: hi ha molta variabilitat.
- Que tanmateix, la llei empírica de l'atzar ens permet controlar
una mica aquesta variabilitat i acostar-nos a la idea de probabilitat.
- El valor de la probabilitat de treure una bola de cada color:
així podeu introduir la regla de Laplace.
- Completeu la revisió de tots els aspectes de la MUD.
- Una vegada assolits els objectius de la MUD anterior, és el moment
de passar a la que s'anomena Endevina què hi ha a la bossa. Es
reprèn l'exercitació anterior però ara amb la bossa tapada. Es fan successives
extraccions de boles d'una bossa i es mostra el gràfic de l'evolució
de les freqüències relatives dels nombres de boles de cada color que
han sortit. Si els nois i les noies han entès bé els continguts
de la MUD anterior, ara poden fer una estimació: a partir de la informació
recollida al gràfic, han d'endevinar la composició de la bossa. Així
reforcen la comprensió de la llei empírica de l'atzar i de la fórmula
de Laplace i, alhora, constaten la possibilitat de fer de manera molt
consistent (ho endevinen molt aviat!) una inferència estadística.
- L'altra MUD que us proposem, El joc de les portes, té en comú
amb les anteriors el fet que es fan servir simulacions per ajudar a
veure quin és el valor d'una probabilitat. A través d'activitats guiades,
es fa una reflexió sobre la probabilitat condicionada.
- La situació és la següent: imagina que engegues la televisió i
veus que el presentador demana a la concursant que triï entre dues
portes, perquè al darrere d'una hi ha el premi del concurs. En aquest
moment, sense cap més dada, tu pots pensar que hi ha el 50 % de
probabilitats que el premi estigui al darrere de la porta 1 i el
50 % de probabilitats que estigui al darrere de la porta 2. I és
del tot cert.
- Però també és ben cert que, habitualment, aquesta fase del concurs va precedida d'una altra. I llavors, amb més dades, el que s'acaba d'enunciar canvia radicalment: hi ha una estratègia favorable per al concursant. Una informació suplementària pot alterar la concepció de la probabilitat.
- Aquesta MUD us ajudarà a entendre molt bé el plantejament probabilístic
d'aquest joc, un exemple clàssic que de vegades es presenta com
una falàcia de les probabilitats però que en realitat podeu veure
(i amb aquesta MUD fer que ho vegin els vostres alumnes) que del
que es tracta és de valorar molt bé tota la informació disponible
abans de calcular probabilitats: aquesta és la idea de la probabilitat
condicionada.
|
|
|
Revisem una aplicació feta en l'entorn
Excel |
| |
|
| |
En aquest apartat us presentem una aplicació feta
amb l'Excel que pot ser útil per fer simulacions de llançaments
de daus i per visualitzar la llei dels grans nombres.
Amb aquesta
aplicació, l'usuari pot simular el llançament de fins a
tres daus. Si es tria el llançament d'un sol dau, es pot analitzar
el cas de les distribucions uniformes, en què tots els valors del
dau tenen la mateixa probabilitat de sortir. Com que el dau pot tenir
diferents casos possibles, pot servir també de suport i comprovació
del càlcul de probabilitats per a diferents resultats teòrics.
En el cas que es triï un màxim de dos resultats possibles
per a un sol dau, es pot identificar la simulació amb el llançament
d'una moneda. En el moment de fer servir més d'un dau, es veu que
la suma dels diferents resultats dels daus ja no té un mateix comportament.
Es pot analitzar, intuïtivament i gràfica, quins esdeveniments
tenen més probabilitat de sortir, si hi ha esdeveniments amb igual
probabilitat, quins són els menys probables, etc. També
es pot comparar la probabilitat teòrica, calculada a part, amb
la distribució de freqüències relatives.
- Recupereu de la carpeta el fitxer PROBABILITAT.XLS i premeu
el botó Habilitar macros per tal que totes les macros
funcionin.
- Premeu el botó Atzar.
- Premeu el botó Daus
nous, entreu a la cel·la H3 un 6 i deixeu en blanc les cel·les
I3 i J3. D'aquesta manera, començareu per la simulació
d'un sol dau convencional.
- Entreu 1.000 a la cel·la
M3 i premeu el botó Llançaments.
- Observeu com es van fent
els 1.000 llançaments i com el gràfic ens indica les diferents
freqüències relatives de cada valor. Si torneu a prémer
el botó Llançaments, es tornen a simular 1.000
llançaments més, els resultats dels quals es van acumulant
als anteriors. Podeu repetir aquest procés variant, si voleu,
el nombre de llançaments (M3).
- Entreu a cada cel·la
del rang E4:E9 la probabilitat de cada valor. En el cas d'un sol dau
de 6 valors possibles, la probabilitat de cada valor és igual
a 1/6.
- Observeu la semblança
numèrica i gràfica entre la freqüència relativa
i la probabilitat, simulant, fins i tot, més llançaments.
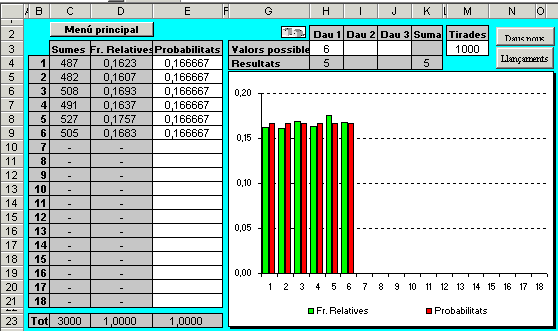
Tot seguit podeu fer la simulació amb dos daus:
- Premeu el botó Daus
nous i introduïu el nombre 6 a les cel·les H3 i I3.
En aquest cas, simulareu el llançament de dos daus, analitzant
les sumes dels diferents valors que van sortint.
- Abans de començar els
llançaments, seria interessant calcular prèviament quina
és la probabilitat per a cadascuna de les sumes possibles. Aquest
és un exercici que pot fer l'alumnat que estigui treballant el
càlcul de probabilitats. Introduïu aquestes probabilitats
a la columna E.
- Premeu diverses vegades
el botó Llançaments i observeu que ara les barres
no tendeixen a igualar-se, com ja es podia intuir observant el gràfic
de les probabilitats introduïdes.
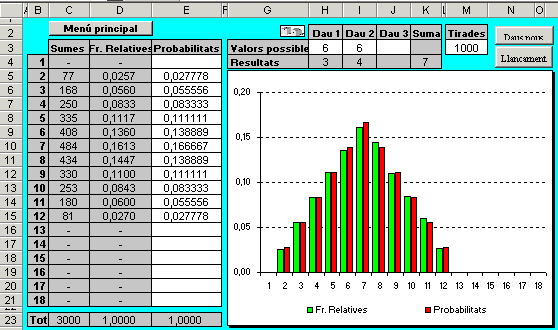
Observeu com s'assemblen els gràfics de les freqüències
relatives i els de les probabilitats.
Podeu fer més simulacions
amb tres daus i variant també els valors possibles de cada dau.
Aquesta última possibilitat fa que simuleu l'experiment de fer
rodar fins a tres ruletes amb diferents valors possibles, tots ells equiprobables,
i calcular la suma dels nombres que van sortint.
|
| |
|
| |
|
 |


