Per enviar les respostes als exercicis elaborareu un document del Word en el qual:

• Posareu un títol per a cada exercici (no cal que hi copieu els enunciats).
• Escriureu les respostes numèriques concretes que es demanen i redactareu, breument, els comentaris adients.
• Inserireu els gràfics que es demanen.

En aquest mòdul heu d'enviar les respostes a un mínim de sis exercicis entre els que es proposen; veureu que alguns fan referència als fonaments de la probabilitat i estan pensats per resoldre's a mà. Llegiu bé les indicacions que expliquen, junt amb els enunciats, quins són els exercicis que heu de trametre, amb el benentès que alguns són obligatoris (aquells que no tenen cap indicació d'opcionalitat); en altres casos heu d'optar entre dues propostes i d'altres són ben bé optatius. Deixeu-nos dir que "no us heu d'espantar" per la longitud dels enunciats de la proposta d'exercicis i que tot seguit es comenten per ajudar-ne a una lectura ràpida.

• Els exercicis en què es concreta el treball amb la distribució binomial (en certa manera el tema central d'aquest mòdul) són el 3 i el 5 que per aquesta raó són obligatoris.
• Per la importància de reflexionar sobre el treball amb un altre model també cal fer un del exercicis 4 (I. geomètrica, que ja hem dit que requeria més treball "manual" o II Poisson). L'altra part es deixa com a opcional... però si heu fet la pràctica 4 completa serà un exercici "molt ràpid".
• En els exercicis 1B i en les dues parts del 2 (que és opcional) es plantegen "problemes senzills de probabilitats". No tenen cap relació amb l'Excel però sí amb la fonamentació conceptual. Els autors del curs pensem que és important incloure propostes com aquestes en la feina del curs, però és possible (i una opinió ben respectable) que algun dels participants en el curs pensi que "no toca" fer aquests exercicis i per això l'exercici 1 té una alternativa que enllaça amb una de les pràctiques del curs.
  

Si heu fet els exercicis obligatoris que s'han comentat fins ara, a saber, una de les dues alternatives de l'exercici 1, el 3, una de les dues opcions del 4 i el 5, "ja haureu complert" si hi afegiu dos exercicis més corresponents a la part fonamental del mòdul (que podeu escollir entre l'altra alternativa de l'1, les dues possibilitats que dóna el 2 o la segona opció del 4.) Tanmateix, encara queden uns altres quatre exercicis opcionals:

• sobre l'ajust a un model (el 6)
• sobre una ampliació d'una pràctica (el 7.I)
• sobre l'elaboració d'una taula de nombres aleatoris (el 7.II, ben interessant)
• i sobre la simulació d'un llançament de monedes (el 7.III)

I en tot cas, ara que heu arribat a l'equador del curs, recordeu que si teniu dubtes, tant dels aspectes del mòdul com dels exercicis obligatoris o com dels d'ampliació, podeu consultar-los per via telemàtica. Procurarem respondre-us amb molt de gust.  

1. Heu d'enviar la resposta a una de les dues propostes següents:
   
   1A. Un comentari sobre la pràctica 1. Això enllaça amb el que la guia del curs esmenta com "un tercer objectiu" del curs (al costat de "l'estadística" i "la informàtica"): aportar idees del punt de vista didàctic.
   
   1B. En una bossa hi tenim 50 boles; 20 són blanques i estan numerades de l'1 al 20; les altres 30 són negres i estan numerades del 21 al 50. Fem l'experiment de treure una bola a l'atzar d'aquesta bossa i considerem els esdeveniments següents:

   B = {bola blanca}     N = {bola negra}
   P = {bola amb número petit, de l'1 al 25, inclosos}
   G = {bola amb número gran, del 26 al 50, inclosos}
   M₂ = {bola amb número parell}    M₃ = {bola amb número múltiple de 3}

   1. Calculeu les probabilitats condicionades següents:
      p(G|B) p(P|B) p(G|N) p(P|N) p(M₂|B) p(M₃|B)
   2. Expliqueu per què G i B són dos esdeveniments mútuament excloents; dieu quina és la probabilitat p(G), compareu-la amb p(G|B) i raoneu si és cert que G i B són dos esdeveniments independents. Ara és el moment de generalitzar el que acabeu de veure i, com es plantejava al document de fonaments, digueu quina paraula falta a la frase següent: Si dos esdeveniments són mútuament excloents, segur que (són?) (no són?) independents.
   3. Doneu un exemple de dos esdeveniments independents entre els que heu estudiat.

2. Podeu enviar opcionalment un dels exercicis següents o bé cap dels dos o bé tots dos:
   1. Fem l'experiment de treure de manera successiva i independent tres boles de la bossa descrita a l'exercici 1. A fi i efecte que les extraccions siguin independents, després d'examinar la bola que hem tret, la tornem a posar a la bossa.
      1. Calculeu la probabilitat que les tres boles siguin blanques.
      2. Calculeu la probabilitat que les tres boles siguin negres.
      3. Calculeu la probabilitat que dues boles siguin negres i una sigui blanca.
      4. Calculeu la probabilitat que dues boles siguin blanques i una sigui negra.
      5. Quant han de sumar les probabilitats calculades? Per què?

   2. Ara considerem l'experiment de treure tres boles alhora de la bossa descrita a l'exercici 1.
      1. Podem assimilar l'experiment al d'extreure tres boles de manera independent? Per què?
      2. En canvi, sí que es pot reflexionar sobre les probabilitats d'aquesta situació si es pensa que es treuen tres boles successivament de la bossa, sense devolució, i que es mira globalment el conjunt de boles obtingudes. Calculeu d'aquesta manera les probabilitats dels esdeveniments descrits a l'exercici 2 i compareu els valors actuals i els que heu calculat allà.

3. Un dau està construït amb el pes mal repartit, de manera que la probabilitat de treure un 6 és 0,25. Es fa l'experiment de tirar 60 vegades aquest dau de manera independent.
   1. Calculeu la probabilitat de treure més de 15 sisos.
   2. Calculeu la probabilitat que surtin entre 10 i 20 sisos (valors inclosos)?
   3. Imagineu que esteu davant d'un grup gran de gent que fa aquesta mateixa experiència. Redacteu una previsió del tipus "com a màxim treureu n sisos cadascú" de manera que el risc d'error en fer la previsió sigui inferior al 10 %.
      Quin és el nombre n més petit que compleix aquesta propietat?

4. Heu d'enviar obligatòriament un dels dos exercicis següents sobre distribucions discretes; l'atre és opcional:
   1. Amb el mateix dau de l'exercici anterior (p(6) = 1/4) es fa l'experiment de tirar-lo repetidament i de manera independent fins que surt un 6.
      1. Calculeu la probabilitat d'haver de tirar menys de 5 vegades.
      2. Si molta gent fes aquesta mateixa experiència simultàniament, al cap de quantes tirades podem pensar a priori que ja hauria acabat el 95 % de les persones que la duen a terme?
         

   2. En una factoria recol·lectora de perles naturals observen que durant un dia, com a mitjana, recullen 4,2 ostres amb perla de qualitat.
      1. Quina és la probabilitat que un dia no recullin cap perla amb ostra?
      2. Quina és la probabilitat que recullin 6 perles o més en un dia?.
      3. Si el departament de propaganda vol fer un anunci que digui "En aquesta factoria recollim cada dia com a mínim n perles", i volen tenir una probabilitat d'encert superior al 80 %, quin ha de ser el valor de n?
         
         

5. Heu de redactar un comentari, il·lustrat gràficament, que permeti comparar els perfils de les tres ditribucions binomials corresponents a n = 30 i valors respectius de p els tres següents: 0,2, 0,5 i 0,8.

   Per fer els gràfics il·lustratius us proposem dues possibilitats:

   • Tal com s'ha exposat a la pràctica 5, feu els gràfics corresponents i copieu-los per separat al document del Word de les respostes.

   • Com a ampliació s'exposa tot seguit el procediment per superposar els tres gràfics, de manera que n'obtingueu un de semblant al següent:
   
   
   

   Sens dubte, aquesta opció il·lustra millor el comentari que feu.

   • Inseriu un nou full de nom Gràfics superposats al llibre DISTRIBUCIONS-DISCRETES.XLS. Escriviu a la primera fila d'aquest nou full, cel·les A1, B1, C1 i D1 els títols descriptius Valor, probabilitat 0,2, probabilitat 0,5, probabilitat 0,8 respectivament.
   • A la columna A, cel·les de la 2 a la 32, poseu-hi els nombres enters del 0 al 30.
   • Accediu ara al full Binomial. Escriviu 0,2 a la cel·la A2 i 30 a la cel·la A4. Seleccioneu ara la columna que dóna les probabilitats (rang C2:C32) i feu Control + C.
   • Aneu al nou full Gràfics superposats, seleccioneu la cel·la B2 i accediu a Edición | Pegado especial | Valores per enganxar només els valors numèrics, sense copiar les fórmules.
   • Repetiu els dos passos anteriors per la distribució de p = 0,5, que enganxareu a la columa C del nou full.
   • Feu-ho una tercera vegada, ara amb els valors corresponents a p = 0,8, i enganxeu-los a la columna D del full Gràfics superposats.
   • Podeu fer servir el diagrama de barres. Així posareu ben bé de manifest el caràcter discret de la distribució estudiada i podreu comparar les tres distribucions estudiades. Per fer aquest gràfic, heu de seleccionar el rang B1:D32 i activar Insertar | Gráficos | Gráfico de columnas; trieu el primer subtipus de la primera fila.
   • Feu clic a Finalizar i fixeu-vos que la retolació de l'eix de les x s'ha posat correlativament, però de l'1 al 31, cosa que no escau. Per corregir-ho, heu de clicar amb el botó dret a l'àrea del gràfic, accedir a Datos de origen | Serie i llavors a Rótulos del eje de categorías (X) heu d'indicar el rang A2:A32 del full Gràfics superposats.
   • Podeu fer altres modificacions al gràfic fins que us agradi la presentació i llavors guardar el llibre.
     
     

6. (Opcional) Redacteu un comentari, acompanyat dels gràfics corresponents, sobre una tasca anàloga a allò que heu treballat a la pràctica 6 per valorar ara, intuïtivament, si la variable que indica el nombre de germans sense comptar l'alumne/a en el fitxer TERCERJM.XLS (és a dir, el resultat de restar 1 a la variable GALUMNE) es pot ajustar bé per una distribució de Poisson, concretament la que té com a paràmetre definidor la mitjana de la variable estudiada.

7. Opcionalment, podeu fer algun dels exercicis següents relatius a simulacions:
   1. (Opcional) Si l'heu feta, comenteu la pràctica d'ampliació que teniu a la pràctica 4. Quines conclusions n'heu tret? Responen a la idea preconcebuda que podíeu tenir del tema?

   2. (Opcional) Es tracta de construir una taula de dígits aleatoris.
      • Obriu un llibre nou de l'Excel.
      • A les 10 primeres cel·les de la columna A escriviu els números del 0 al 9. A les 10 primeres cel·les de la columna B, al costat dels valors anteriors, escriviu el valor uniforme 0,1. Ja tenim preparats els valors i probabilitats per escriure la taula de dígits aleatoris.
      • Accediu a Análisis de datos | Generación de números aleatoris i feu 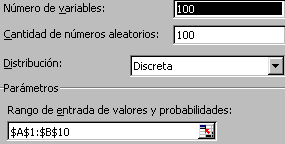i indiqueu que els resultats es posin en un full nou.
      • En aquest full nou teniu una taula de 10.000 nombres aleatoris.

      Ara ara us suggerim una simulació manual.
      Escolliu a l'atzar, de la manera que us sembli més convenient, un dígit dels que apareixen a la taula. A partir d'aquest nombre que heu seleccionat, mireu els 20 dígits següents i feu el recompte del nombre de 0 que trobeu.

      1. Aquest nombre de zeros, a quina distribució s'ha d'ajustar?
      2. Feu l'experiment anterior 10 vegades i transcriviu els resultats dels comptes del nombre de zeros obtinguts.
      3. Creieu que es corresponen amb els resultats esperats?

   3. (Opcional) Volem fer una simulació que consisteix en 2.000 repeticions de l'experiment de llançar de manera independent 5 monedes perfectament equilibrades.
      1. Quin és el model teòric d'aquesta experiència?
      2. Feu una simulació d'aquest experiment amb l'Excel.
      3. Estudieu la variable que resulta i transcriviu-ne la taula de valors.