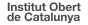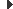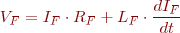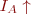Maniobres en els motors de corrent continu

En el moment d’arrencar un motor de CC es poden produir grans intensitats pel fet que en partir del repòs (ω_m = 0), la força contraelectromotriu E_A = 0, i per tant la intensitat està únicament limitada per la R_A, la resistència del bobinatge del rotor, que sol ser molt petita.

Considereu un motor de V_T = 300 V, amb R_A = 0,2 Ω. En el moment d’arrencar hi passarà una intensitat.

El reglament de baixa tensió limita les intensitats d’arrencada dels motors per l’efecte que poden tenir a la xarxa elèctrica. Per altra banda, els motors de CC s’han de protegir de possibles eventualitats que puguin fer malbé el motor o la instal·lació a la qual es connecten. En particular s’han de protegir contra el següent:

1. Danys produïts per curtcircuits o rotor parat
2. Danys per sobrecàrregues prolongades
3. Danys per I_arr excessives

Una possibilitat per disminuir I_arr és interposar una resistència en sèrie amb el bobinatge per limitar aquesta intensitat al valor desitjat fins que el motor comenci a girar i faci que E_A sigui suficientment gran per limitar la I_arr al valor desitjat.

Aquesta resistència consumirà una potència elevada i, per tant, només s’ha de connectar al moment de l’arrencada i després s’ha de treure del circuit; per tant, no s’ha d’utilitzar com un mètode de regulació de velocitat en el cas de motors amb potències grans, pel seu cost econòmic.

Habitualment aquesta resistència està formada per una sèrie de trams que es van curtcircuitant a mesura que el motor va adquirint més velocitat. D’aquesta manera s’optimitza el temps d’arrencada d’un motor. La figura mostra aquestes resistències.

El control del circuit d’arrencada que faci que es tanquin els contactes 1_A, 2_A i 3_A pot ser un PLC (autòmat programable) o un circuit amb contactors i temporitzadors clàssic. A la figura es mostra un possible circuit amb contactors.

Com podeu observar a la figura, el circuit sencer està protegit amb dos fusibles F₁ i F₂. Les dues primeres línies horitzontals representen el motor de CC. En el circuit de camp podem veure el cercle marcat amb FL que representa un contactor de pèrdua de camp. Un contacte d’aquest contactor el podem veure en sèrie amb el motor de CC, de manera que si s’obre el circuit d’excitació, es talla el subministrament d’energia al motor, ja que si no, s’embalaria excessivament. També hi podem veure un relé OL de sobrecàrrega, que es dispara (obre el circuit) si detecta una sobrecàrrega prolongada en el circuit.

El circuit de maniobra està protegit per dos fusibles més, F₃ i F₄, i consta d’un circuit d’engegada-aturada clàssic. Si es prem el polsador de marxa, s’engega el motor i es realimenta amb el contacte M, de manera que ja podem deixar de polsar la marxa i el motor queda funcionant.

A partir del moment que el motor es posa en marxa, comença a temporitzar l’1_TD. Acabada la temporització, tanca el contacte 1_TD curtcircuitant el primer tram de la resistència d’arrencada. En aquest instant comença la segona temporització, que tancarà el contacte 2_TD, i el mateix amb la tercera. Un cop acabades les tres temporitzacions, observeu que el motor queda connectat a la tensió d’alimentació i ja queden desconnectats tots els trams de resistència d’arrencada.

Una versió millorada d’aquest esquema substitueix els temporitzadors per sensors de la velocitat del motor. Això fa que els trams de resistència connectats en sèrie amb el bobinatge del rotor vagin sortint del circuit a mesura que la velocitat del motor vagi arribant al punt exacte que permeti l’extracció del tram corresponent i sigui independent de la velocitat d’acceleració del motor.

Els generadors de CC són màquines de CC que s’utilitzen com a generadors. Actualment no se solen utilitzar les màquines de CC per subministrar energia elèctrica en forma de CC. Si es necessita aquest tipus d’energia elèctrica en forma de CC se solen utilitzar rectificadors d’estat sòlid per obtenir-la. No obstant això, la màquina elèctrica és reversible, o sigui, que si l’energia s’absorbeix pels bobinatges en forma d’energia elèctrica i se subministra per l’eix en forma d’energia mecànica tenim un motor, però si fa el camí invers, tenim un generador. És per això que un tramvia que puja un pendent empès per un motor de CC utilitza la màquina com a motor, però quan arriba una baixada, la mateixa màquina es converteix en un generador de CC i ara es pot emmagatzemar l’energia elèctrica que produeix. Per tant, és important conèixer com es comporta i com es pot regular per utilitzar convenientment aquesta energia.

El generadors d’excitació independent són aquells en què els bobinatges inductor i induït estan alimentats per fonts de CC independents.

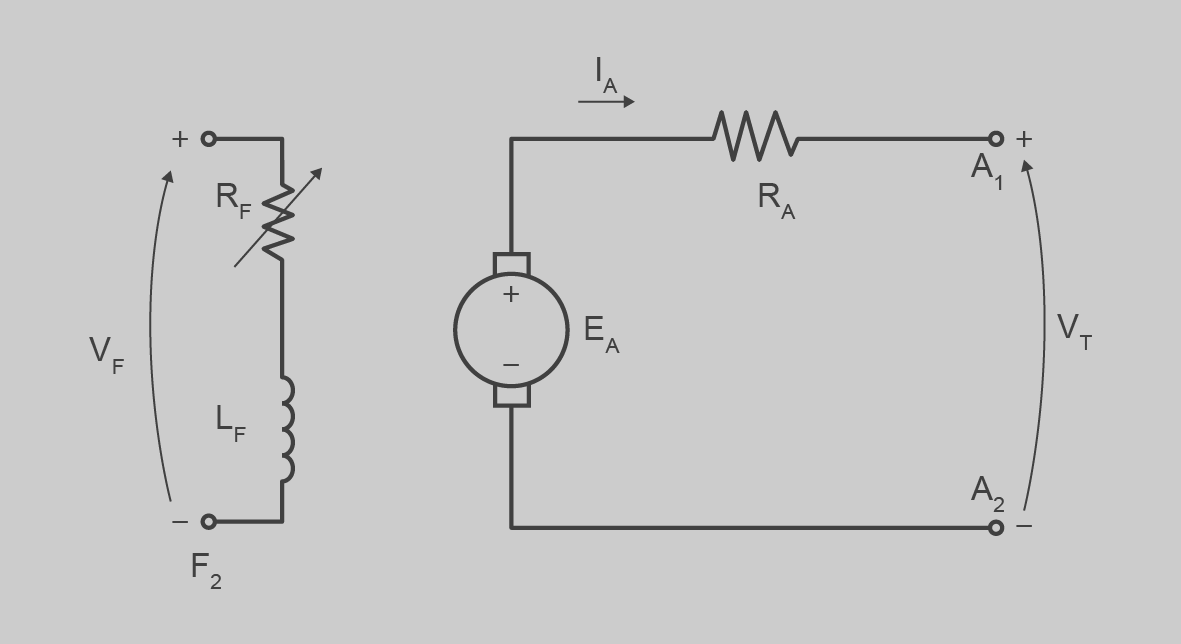
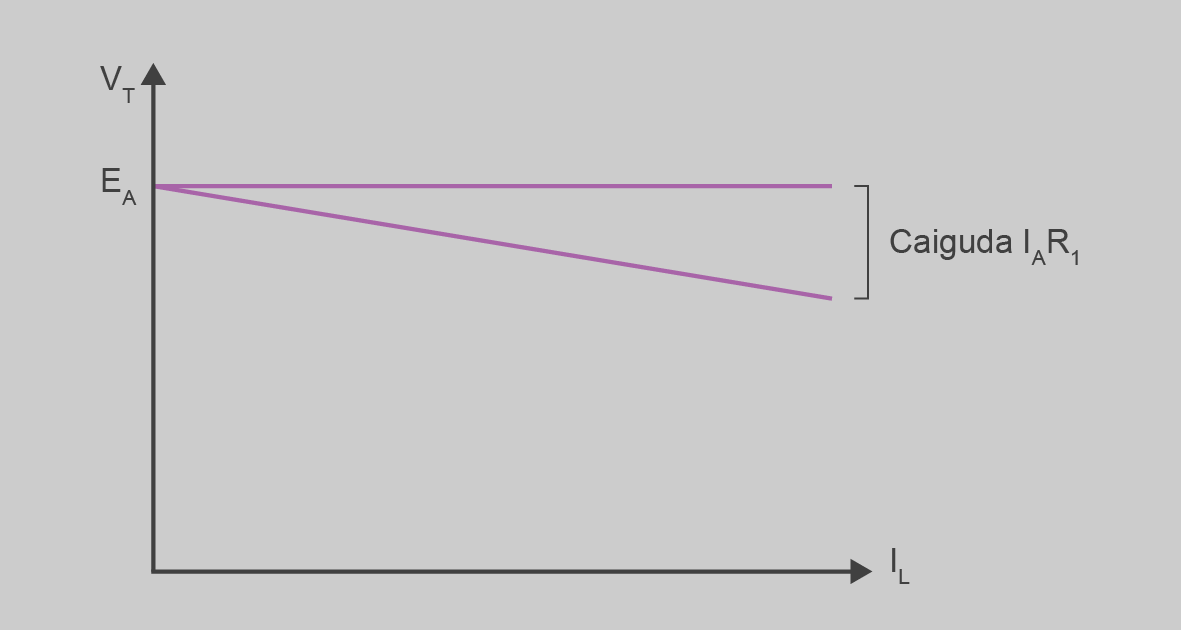
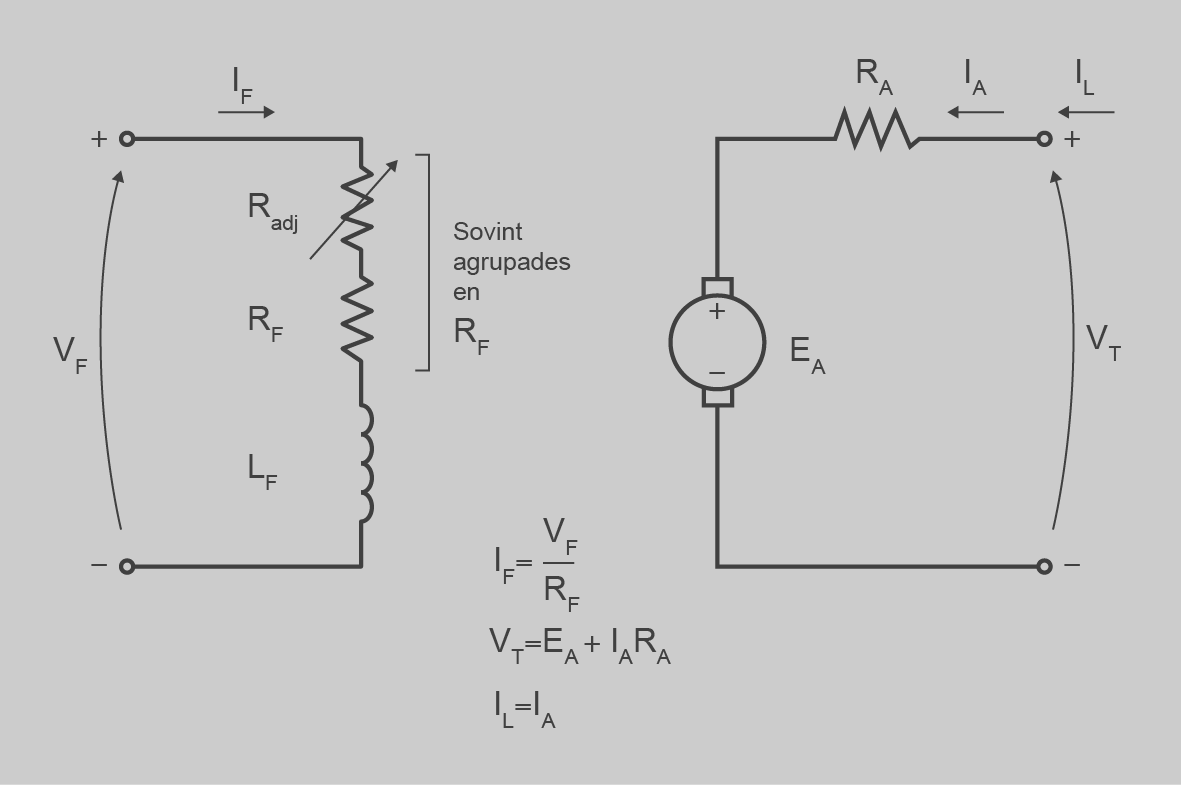
La figura mostra el circuit equivalent d’un generador d’excitació independent, d’on es poden deduir les equacions següents:

Si es posa càrrega al generador hi passa una I_L = I_A que produeix una caiguda de tensió a la resistència R_A, i disminueix la tensió de sortida. A la figura podem veure aquest efecte.

El voltatge en els terminals de sortida es pot modificar variant la E_A, o sigui, el voltatge que subministra el generador en buit.

Atès que E_A = K·Φ·ω_m, podem variar aquesta tensió modificant la I_F (el Φ) o variar la velocitat ω_m.

La I_F es pot variar modificant la tensió del bobinatge de camp, o modificant el valor del reòstat situat en sèrie amb el circuit d’excitació R_F.

Si disminuïm R_F s’incrementa la I_F:

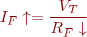
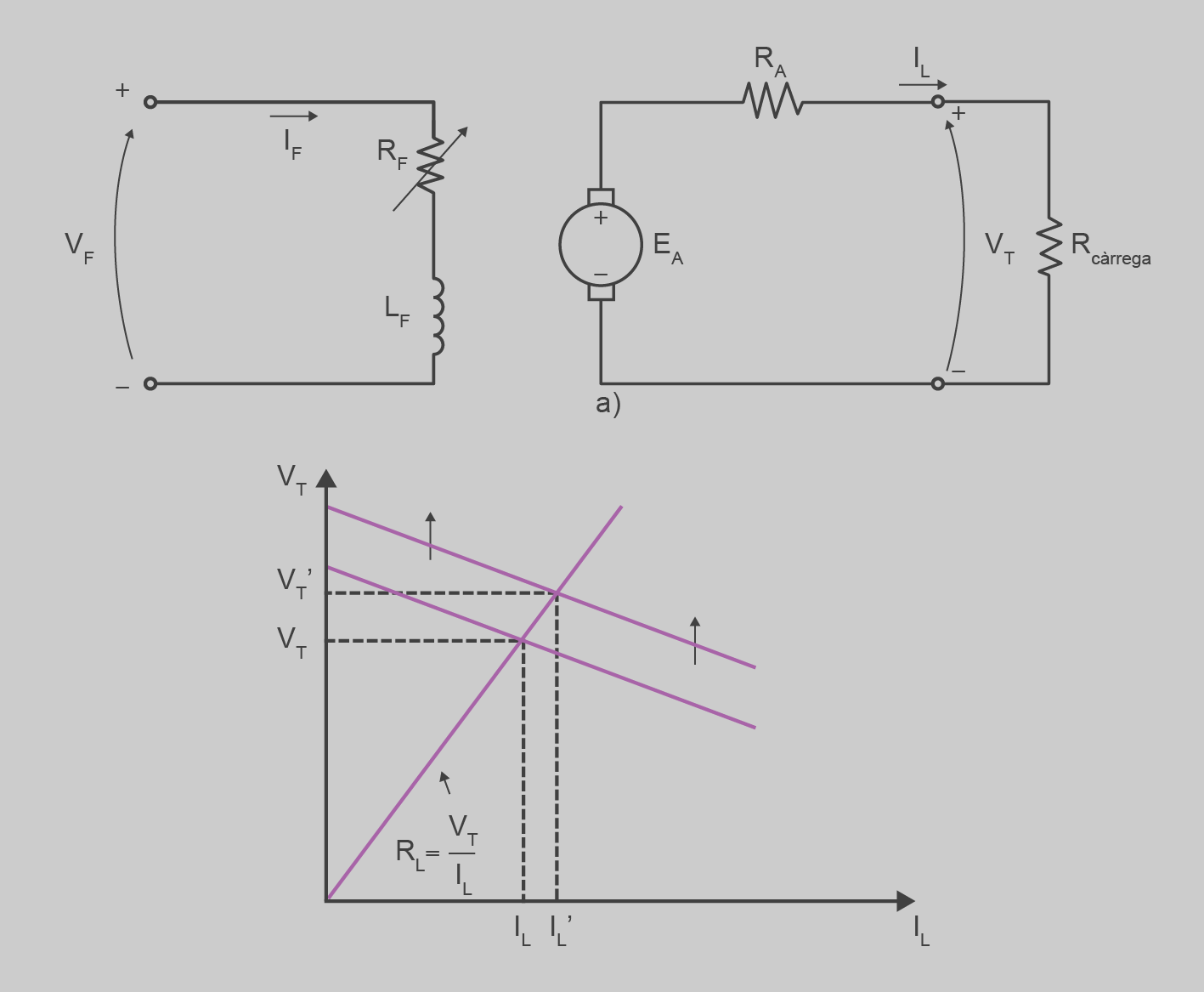
Això provoca un increment de E_A, i finalment, un increment de V_T:

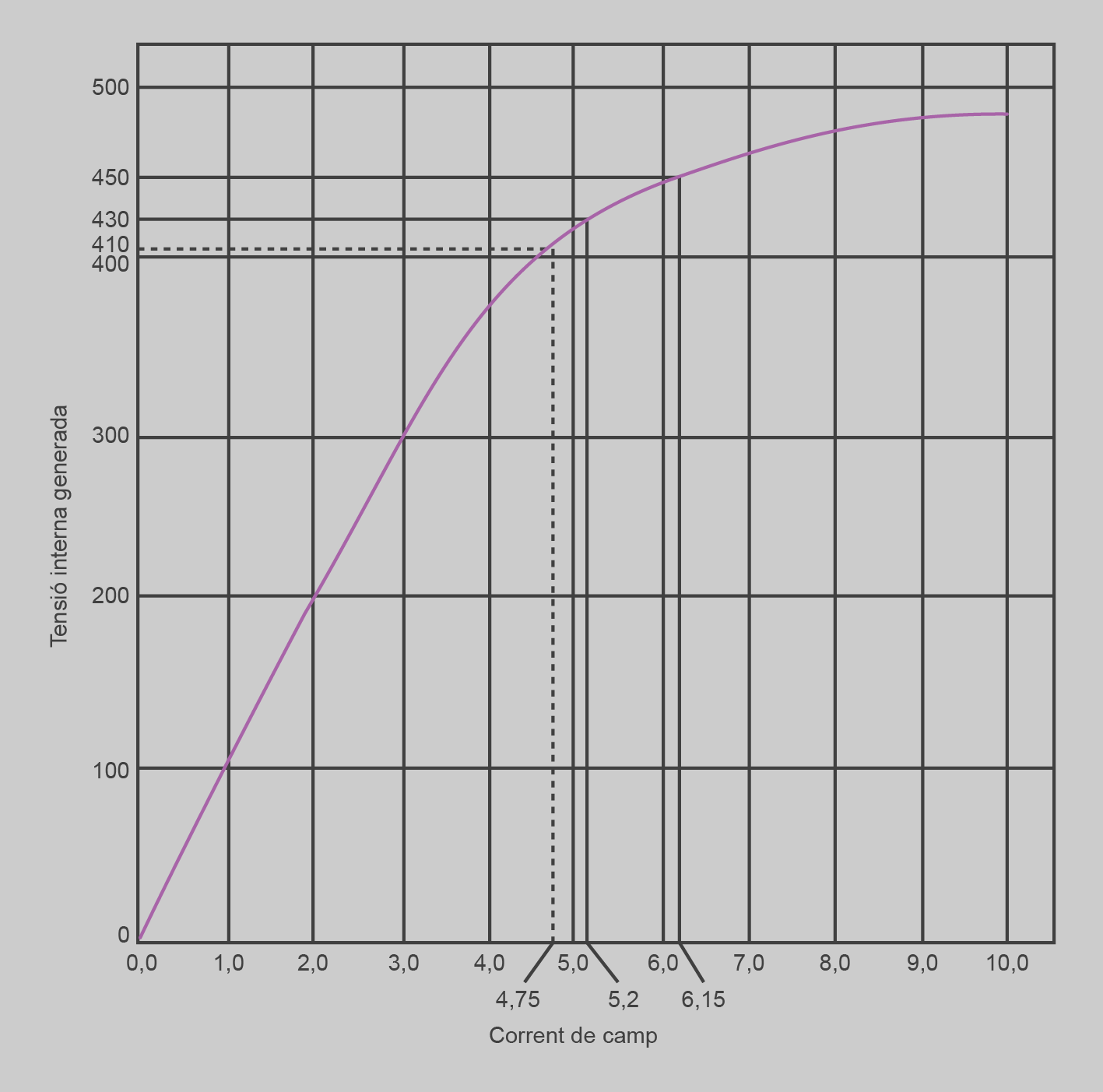
La figura mostra com s’incrementa el voltatge terminal V_T en incrementar la E_A. Observeu que en incrementar-se la E_A, la recta es desplaça cap amunt i, per tant, la tensió de la càrrega passa de V_T a V’_T.

Aquesta variació de la E_A es pot considerar lineal mentre la màquina no se satura. Si l’excitació és tal que va més enllà del colze de saturació, veiem que en incrementar I_F es produeix un increment del flux magnètic menor i, per tant, una variació menor de la tensió E_A. Per tant, aquesta regulació només és una regulació lineal en el tram lineal de la corba de saturació. A la figura podem veure aquest efecte.

En les aplicacions habituals, l’element que fa girar l’eix del generador de CC no admet gaire regulació de velocitat, i per això la regulació de la tensió en borns mitjançant la variació de velocitat no s’utilitza gaire. No obstant això, com la tensió en buit del generador E_A és proporcional a la velocitat, també la tensió en borns del generador V_T variarà en variar la velocitat de l’eix.

En un motor de CC entra energia elèctrica pels bobinatges i surt energia mecànica per l’eix, que podem utilitzar per moure càrregues, posicionar eines, etc. En l’energia mecànica tenim dues magnituds fonamentals que ens interessa conèixer. Són el parell, que simbolitzarem amb la lletra grega τ (tau minúscula), i la velocitat de gir, que simbolitzarem amb la lletra grega ω (omega minúscula). Com el parell és una força per una distància, s’expressa en N·m (newtons metre) i la velocitat angular en rad/s (radians per segon), tot i que encara és molt utilitzada la unitat de voltes per minut o revolucions per minut. La relació entre les dues unitats de velocitat de rotació és:

Habitualment el parell en l’eix del motor està determinat per la càrrega que li posem. En canvi, podem modificar la velocitat de gir de diverses maneres.

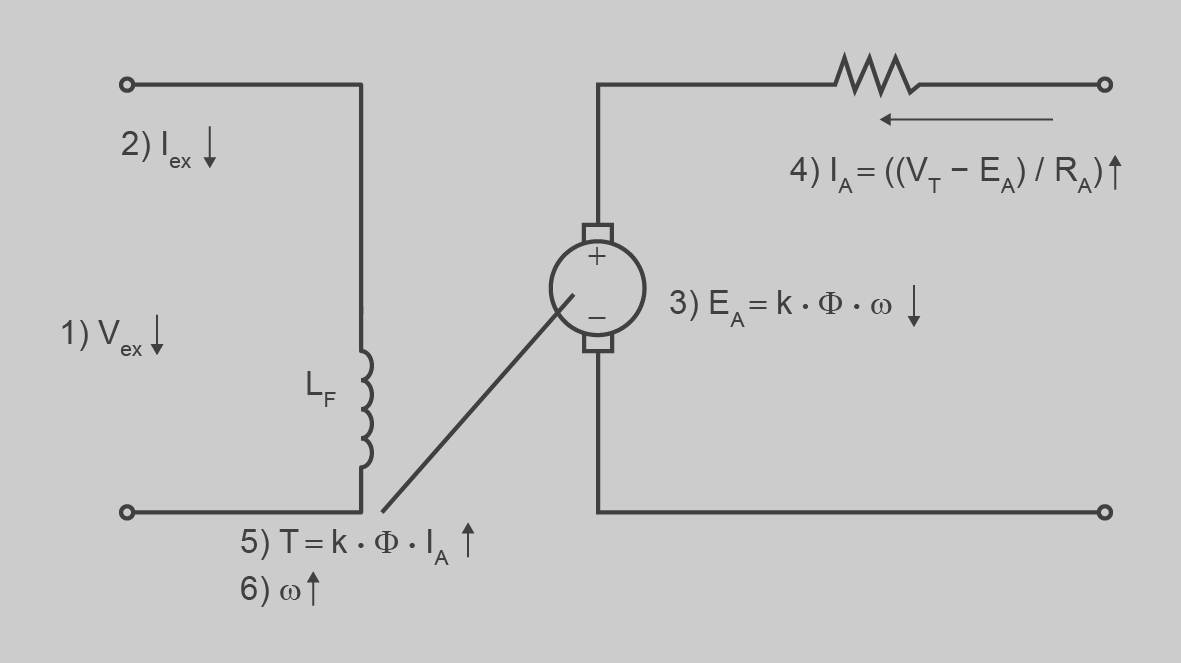
Els motors d’excitació independent i d’excitació en paral·lel es comporten de manera similar respecte a la variació de velocitat. En aquest cas ens centrarem en els motors d’excitació independent. A la figura podem veure l’esquema equivalent d’aquest motor.

Per veure com es pot modificar la velocitat, ho fem relacionant les fórmules que descriuen el comportament del motor:

Com que:

Podem escriure que:

En el cas del motor d’excitació independent, el parell és:

D’on podem extreure el corrent I_A:

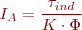
Així, en total tenim:

d’on podem obtenir una expressió per a la velocitat de gir:

Aquesta darrera equació ens mostra la relació entre la velocitat angular i les variables de les quals depèn. Per tant, podem deduir que per variar la velocitat angular podem modificar els valors de V_T, Φ (o sigui, I_F i R_F) i R_A.

Com R_F és la resistència dels bobinatges del rotor, no es pot modificar directament, però sí que es pot posar una resistència exterior en sèrie. Variant cada una d’aquestes magnituds, tenim una regulació de característiques diferents. La variació de R_A només es pot fer en motors de poca potència o en una regulació molt limitada en el temps.

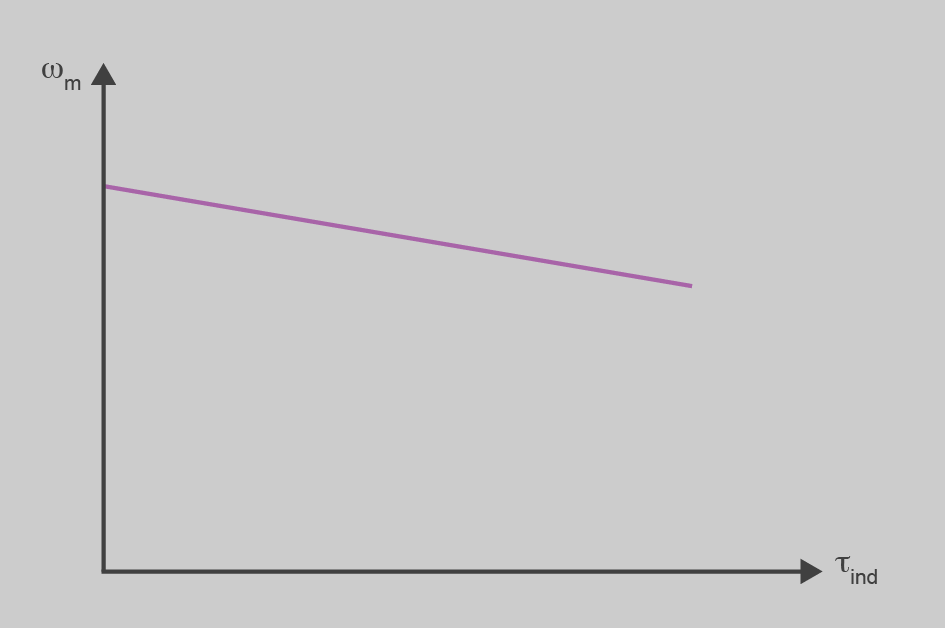
Si mantenim constant tant la I_F com la V_T, la relació entre la velocitat i el parell és una línia recta. A la figura podem veure representada aquesta relació.

En realitat la velocitat no varia gaire amb el parell. Es diu que els motors de CC d’excitació independent i en paral·lel tenen una característica de velocitat dura, perquè la velocitat en càrrega és semblant a la de buit.

Exemple de càlcul de la variació de la velocitat d’un motor de CC d’excitació independent en variar el parell carregat a l’eix

Es disposa d’un motor de CC d’excitació independent amb un R_A = 0,15 Ω. S’alimenta a una tensió V_T = 300 V que es manté constant, i en el circuit d’excitació tenim una V_F = 300 V mentre gira a 1.200 rpm. El motor consumeix una I_A = 80 A i una I_F = 1 A. Si el parell de càrrega s’incrementa un 30%, calculeu la nova velocitat.

Solució

La situació inicial es mostra a la figura següent:

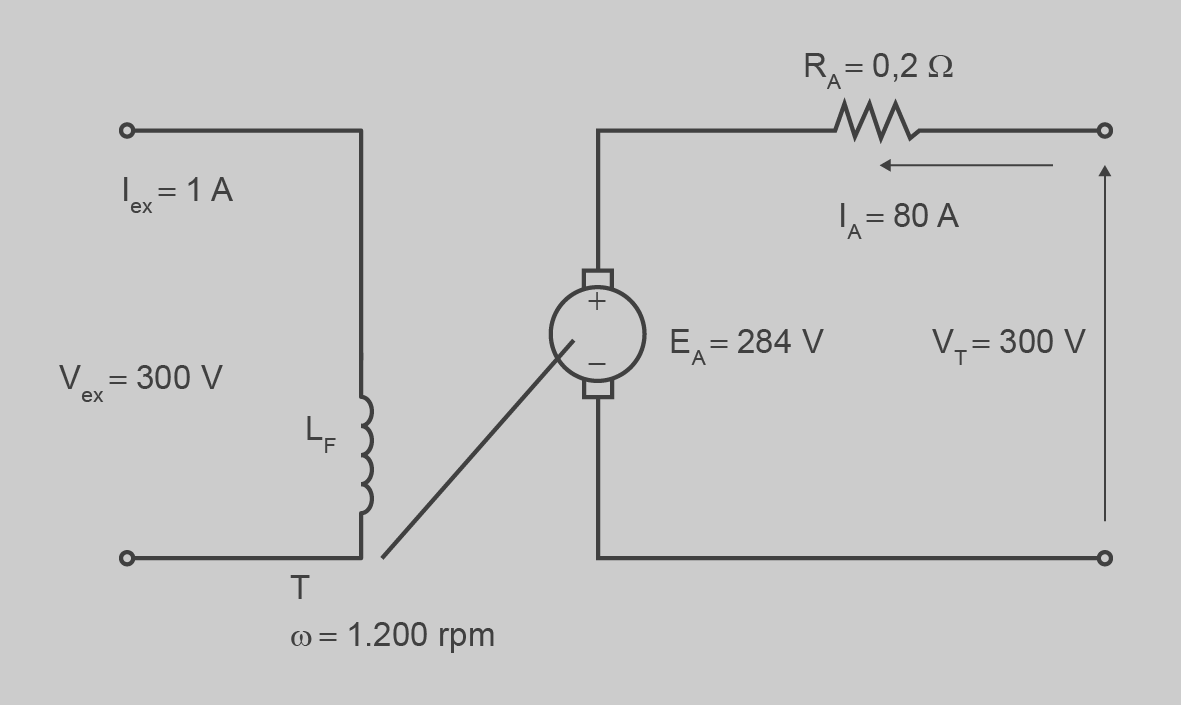
Podem calcular la E_A = 300 − 0,2 · 80 = 284 V

Com el parell de càrrega s’incrementa un 30% tenim una nova I_A’:

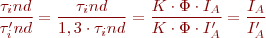
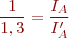
D’on podem trobar:

I la nova E_A’ = 300 − 104 · 0,2 = 279,2 V

Ara, comparant les forces contraelectromotrius:

D’on:

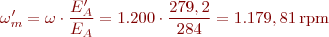
A la figura següent hi ha la situació final del problema:

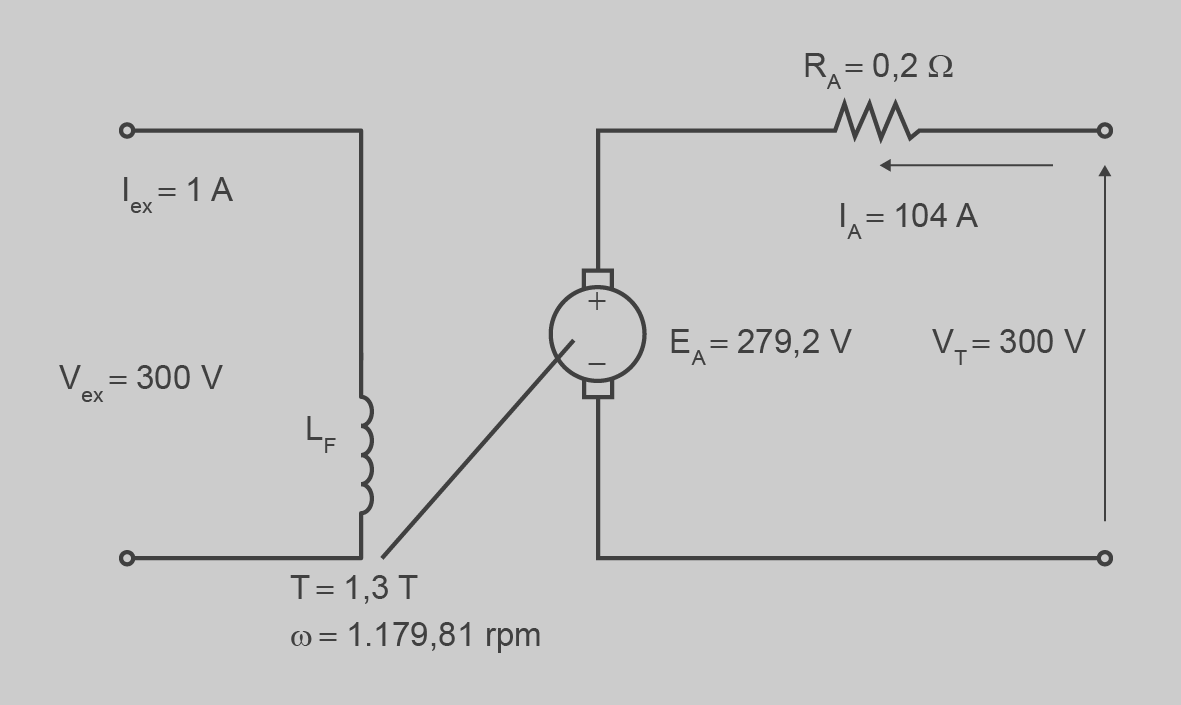
Per tant, en incrementar el parell un 30% hem obtingut una disminució de la velocitat del motor fins a 1.179,81 rpm. Podem observar que un fort increment del parell produeix un decrement relativament petit de la velocitat del motor. Per això es diu que el motor de CC d’excitació independent o en paral·lel tenen una característica dura.

Hi ha dues maneres de variar la I_F i, per tant, el flux de la màquina:

1. Modificant la tensió del bobinatge d’excitació: com més tensió, més intensitat i, per tant, més flux.
2. Posant en sèrie amb el bobinatge un reòstat R_F variable: en modificar el seu valor, també fem variar la I_F.

Partim de l’expressió de la velocitat:

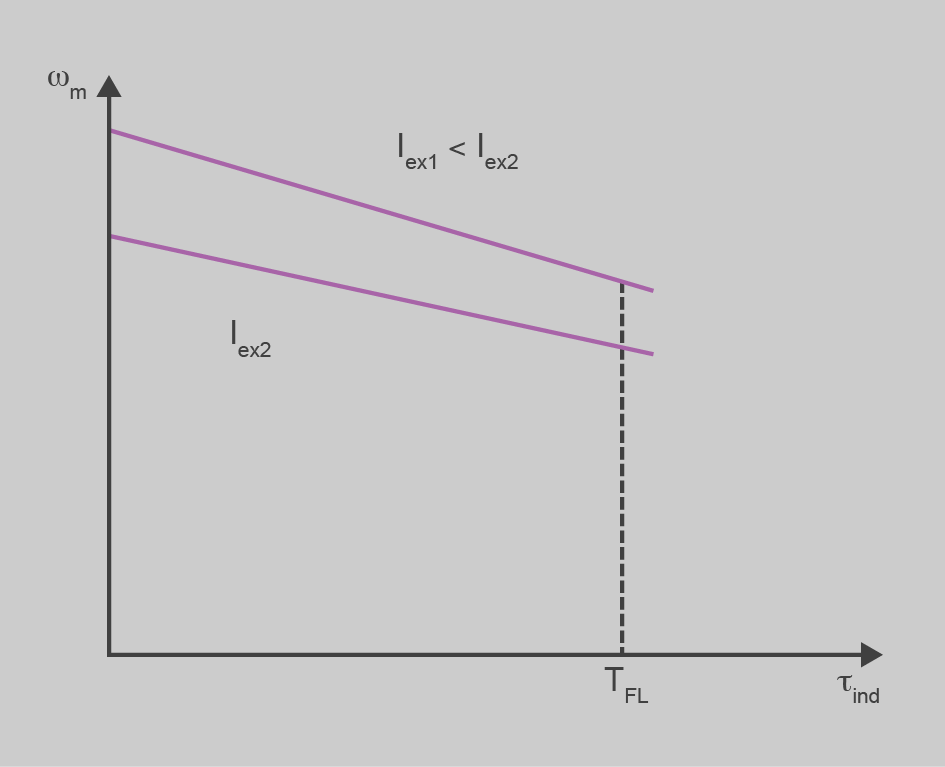
Veiem que si disminuïm el flux, el primer terme de la velocitat s’incrementa, i també el segon i, per tant, la recta es desplaça cap amunt i té un pendent més gran. A la figura podeu veure aquest efecte. Per a un mateix parell de càrrega, en disminuir la I_F, la velocitat s’incrementa.

Com podeu veure, en aquest tipus de control podem incrementar la tensió del bobinatge inductor (increment de I_F i de flux) per disminuir la velocitat del motor o decrementar-la (decrement de I_F i de flux) per incrementar la velocitat. En aquest darrer cas, podem reflexionar sobre els efectes de portar el control al límit, o sigui, disminuir la V_F i per tant la I_F i el flux associat. En aquest cas podem deduir que quan la E_A es fa com més va més petita, la I_A s’incrementa. El dubte sorgeix en considerar si el parell, que depèn de la I_A i el flux (τ_ind = k · · I_A), s’incrementa o disminueix. Hem de dir que amb els valors habituals de la R_A i la corba d’histèresi del motor, la combinació descrita causa un increment important del parell. Així doncs, el parell i, per tant, la velocitat del motor, s’incrementen en disminuir la V_F.

Podríem posar la concatenació d’efectes següent:

A la figura podeu veure aquesta concatenació d’efectes en un esquema del circuit.

Si aquesta reducció es porta el límit, o sigui, que es deixa el motor sense flux (I_F = 0), podem tenir una velocitat de buit molt gran que, si no salten les proteccions del motor, en poden produir la destrucció. És per aquest motiu que els motors d’excitació en sèrie o en paral·lel s’han de protegir amb un relé de pèrdua de camp.

És aconsellable que el circuit de control del motor porti sempre un contacte que n’impedeixi l’alimentació si no hi ha intensitat I_F, o sigui, si prèviament no s’ha excitat el motor. La figura mostra part del circuit de control d’arrencada d’un motor de CC, on s’ha inclòs el contacte del relé FL que assegura que el motor només estarà alimentat si prèviament hi ha intensitat al bobinatge de camp.

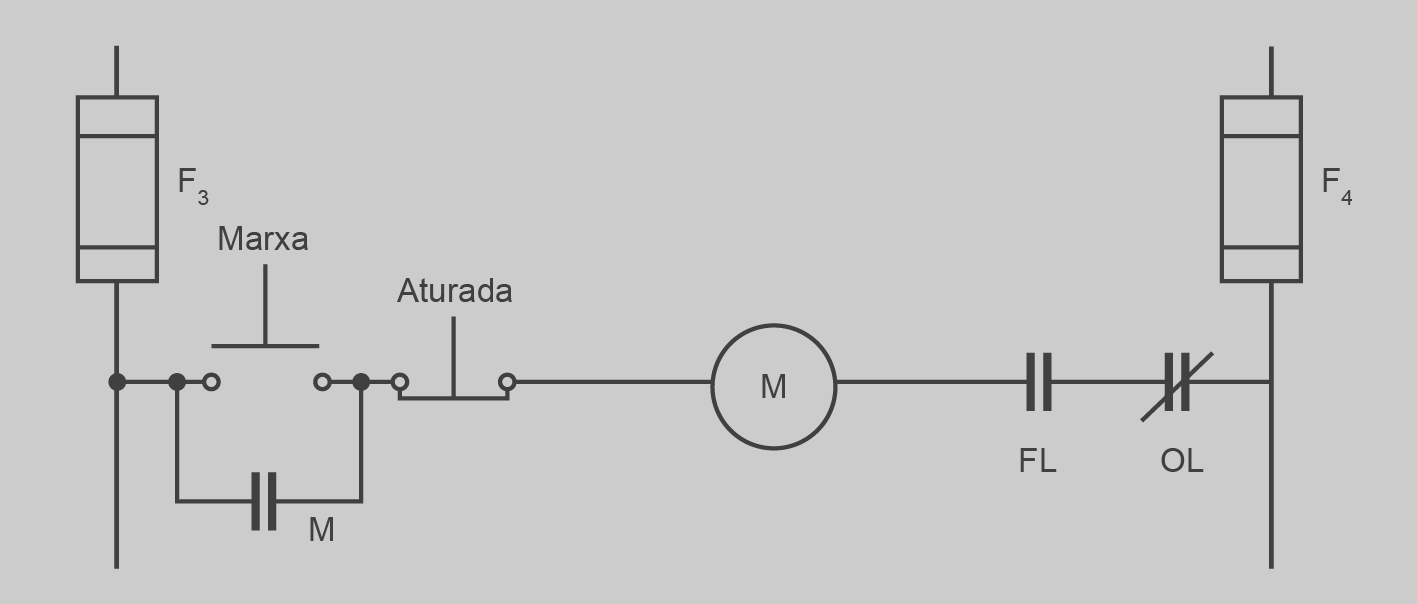
Per tant, en el moment d’arrencada d’un motor, l’ordre d’operacions ha de ser:

1. Excitació del bobinatge inductor o de l’estator
2. Excitació del bobinatge induït o del rotor, condicionat que s’hagi fet l’operació anterior.

En el cas de motors d’excitació en sèrie o composta, no hi trobem habitualment el problema de pèrdua de camp, perquè en estar tots dos bobinatges en sèrie, sempre que hi hagi alimentació a l’induït, hi haurà corrent per l’inductor i, per tant, flux a la màquina.

Exemple de càlcul de la velocitat d’un motor de CC d’excitació independent en variar la tensió d'excitació

Es disposa d’un motor de CC excitació independent amb un R_A = 0,2 Ω. S’alimenta a una tensió V_T = 300 V que es manté constant, i en el circuit d’excitació tenim una V_ex = 300 V mentre gira a 1.200 rpm i consumeix una I_A = 80 A i una I_F = 1 A. Si el parell de càrrega es manté constant, calculeu la nova velocitat si disminuïm la V_F fins a 250 V.

Solució

La situació inicial es mostra a la figura següent:

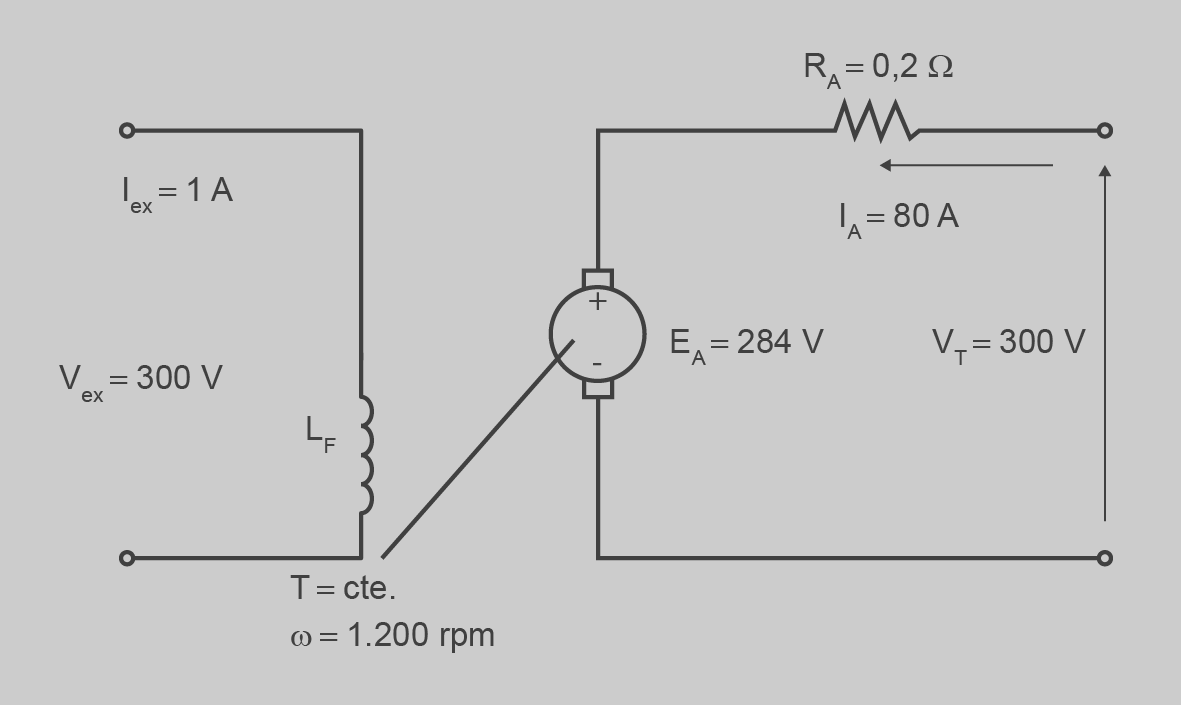
Podem calcular la .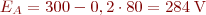

Com el parell de càrrega és constant, la nova I_A’ val:

Considerem que el motor treballa en zona lineal, i per tant el flux és proporcional a la V_F, i per tant tenim:

• 
• 

I ara:

D’on podem extreure el valor del corrent I_A’: I_A’ = 96 A.

I la nova

Ara, comparant les E_A:

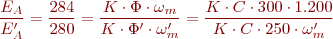
D’on:

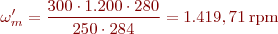
A la figura següent es veu la situació final del problema:

Per tant, en disminuir el flux hem incrementat la velocitat del motor de 1.200 a 1.419,71 rpm.

Observeu l’expressió de la velocitat del motor:

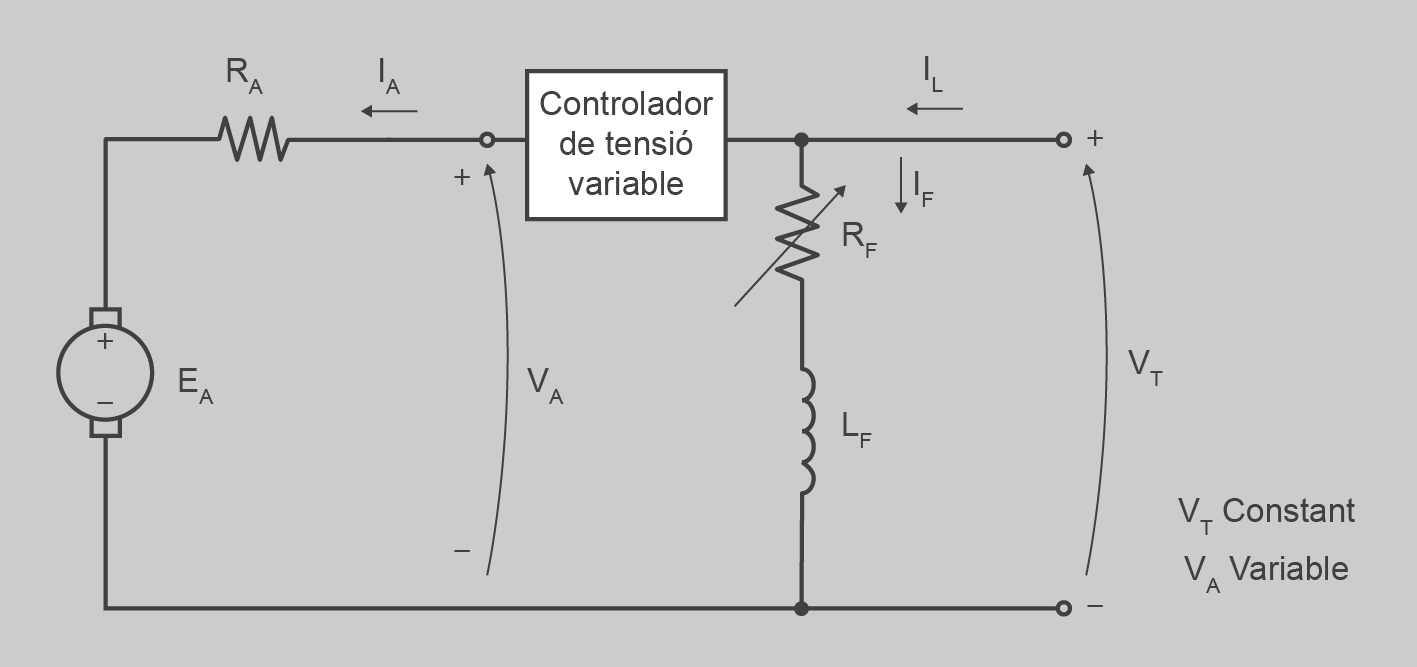
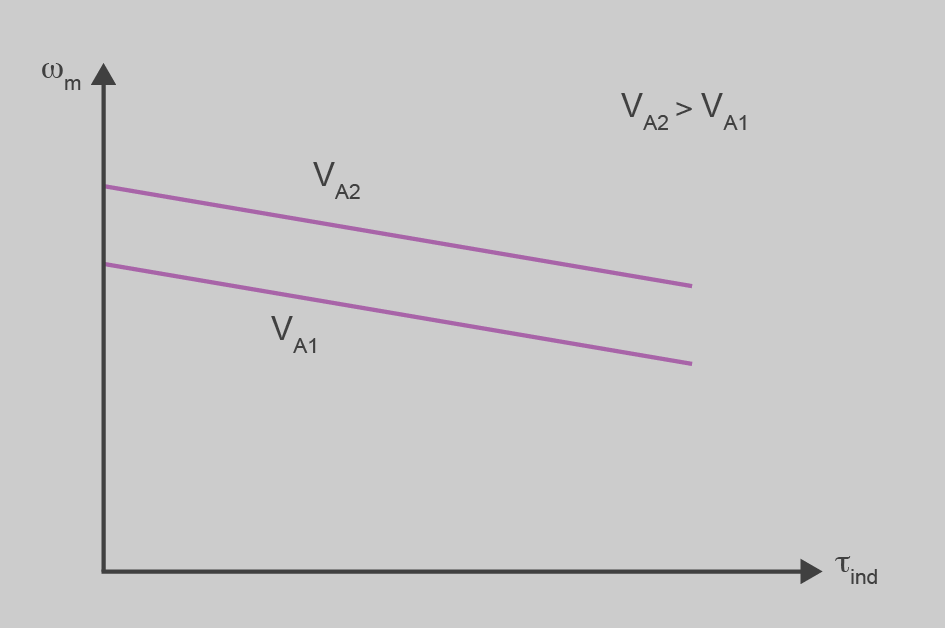
Hi podeu veure que si incrementem o decrementem V_T, la recta es desplaçarà cap a dalt o cap a baix i, per tant, modificarem la velocitat final del motor per a un parell de càrrega determinat. Per aconseguir aquesta variació sense modificar la tensió de l’estator (I_F = constant), es connecta el bobinatge d’excitació a la tensió V_T sense regular, i amb una font controlada de tensió modifiquem només el valor de la tensió al rotor de la màquina. A la figura podeu veure el circuit per aconseguir-ho.

La figura mostra la variació de velocitat de la màquina de CC en variar V_T.

Exemple de càlcul de la velocitat d’un motor de CC d’excitació independent en variar la tensió VT

Es disposa d’un motor de CC d’excitació independent amb una R_A = 0,15 Ω. La tensió del bobinatge de camp V_F es manté constant. S’alimenta a una tensió de V_T = 300 V i gira a 1.200 rpm, mentre consumeix una I_A = 100 A. Calculeu la nova velocitat si es disminueix la V_T fins a 250 V.

Solució

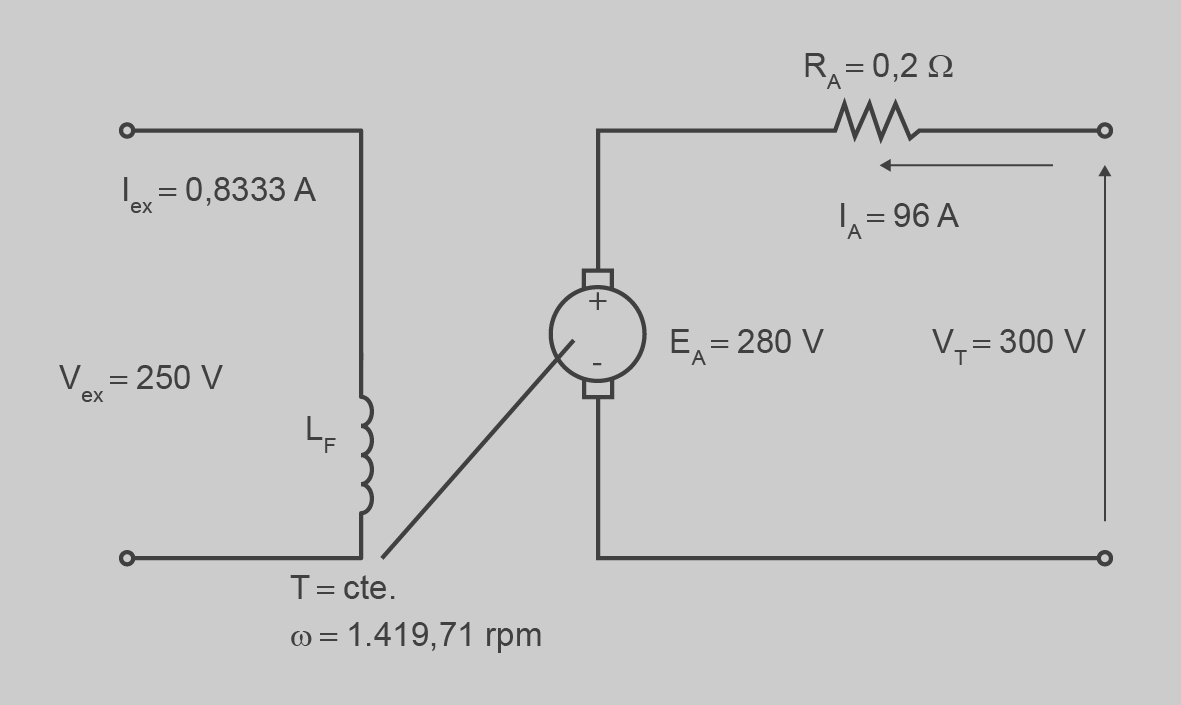
La situació inicial es mostra a la figura següent:

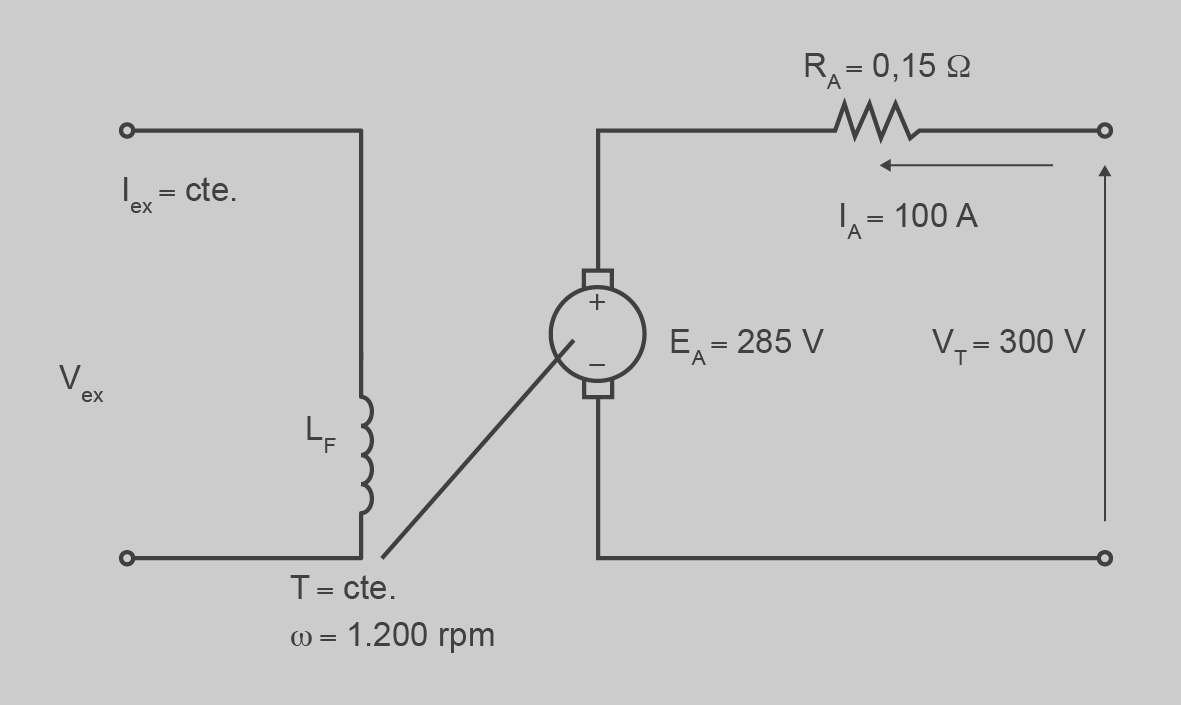
Podem calcular la E_A = 300 − 0,15 · 100 = 285 V

Com més va més s’utilitzen programes d’elements finits per dissenyar i o analitzar tota mena de dissenys. L’anàlisi de circuits elèctrics no és una excepció. Aquí podreu veure la simulació d’aquest exemple, que utilitzarem com a comprovació del càlcul analític de la situació inicial i la final del problema.

Si tenim en compte que E_A = K · · ω_m i que amb la nova situació, E_A’= K’ · · ω_m’, podem dir que:

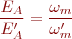
I d’aquí:

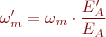
Per trobar la nova E_A’ considerarem que si el parell es manté constant, vol dir que la I_A també es manté constant a 100 A, i per tant la nova força contraelectromotriu serà:

Així:

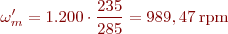
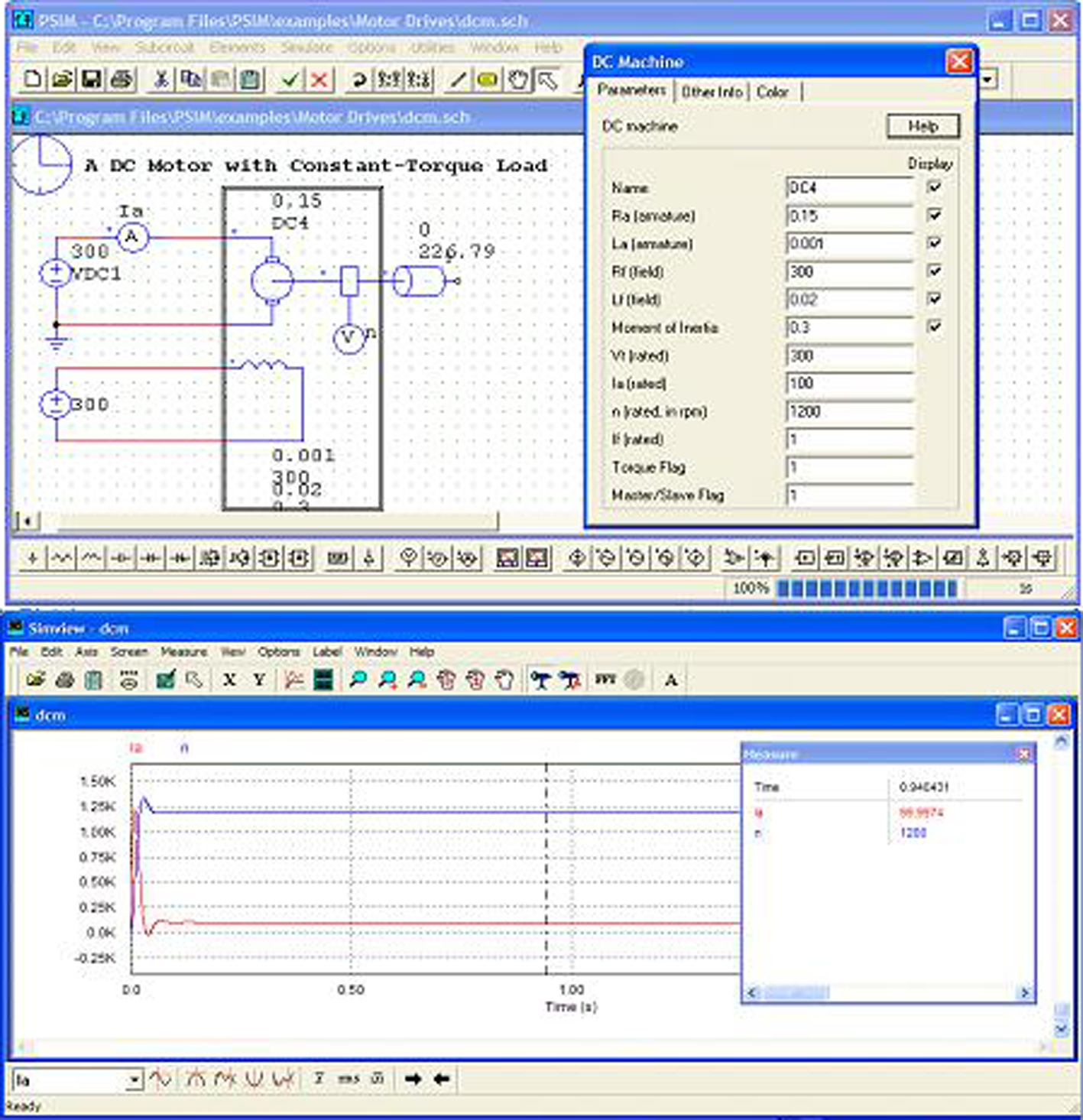
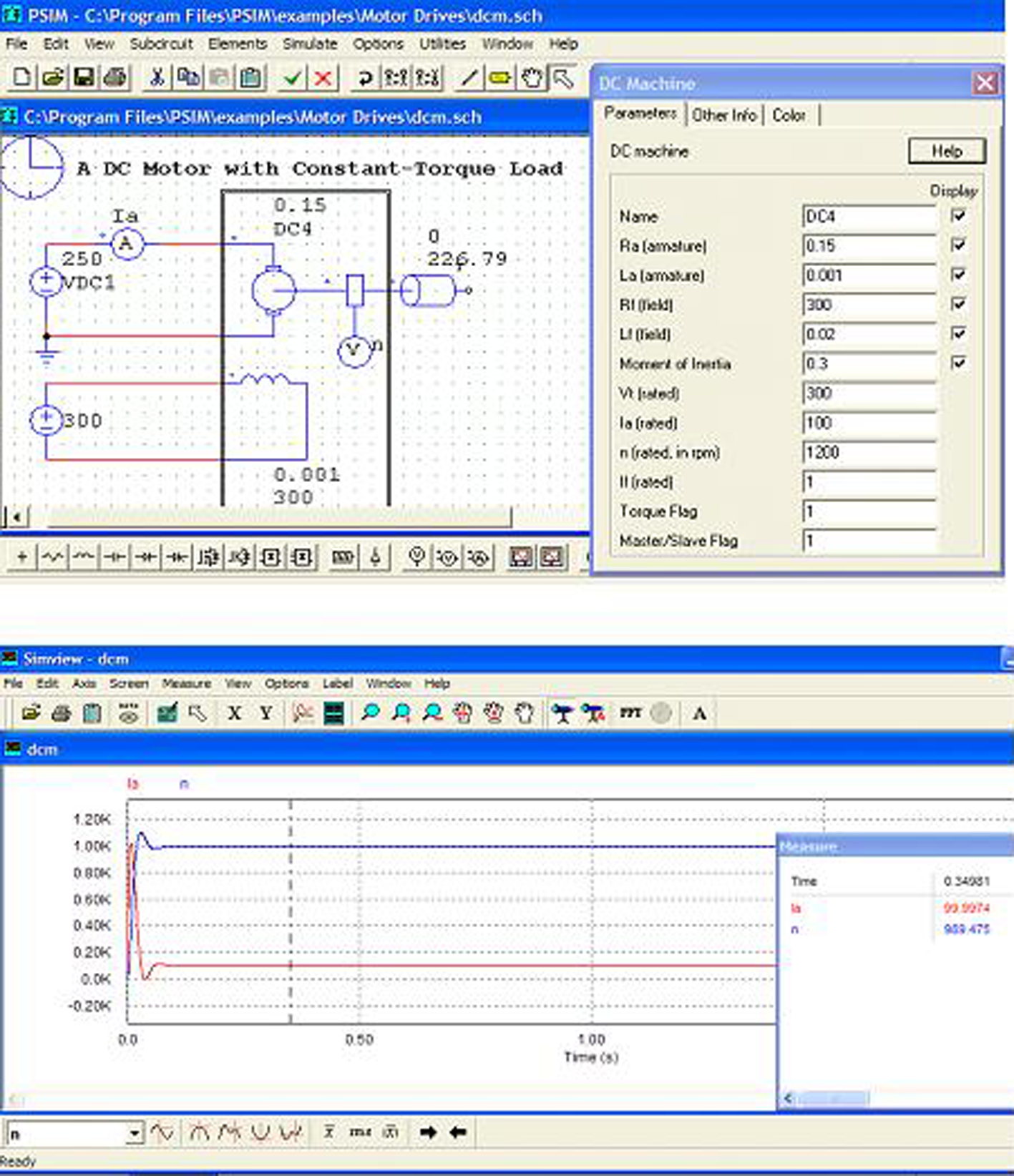
A la figura següent podeu veure la simulació d’aquest motor amb el programari lliure PSim i el resultat d’aquesta simulació. Observeu els valors del motor i el parell e resistent a l’eix:

La figura següent mostra la situació final del problema:

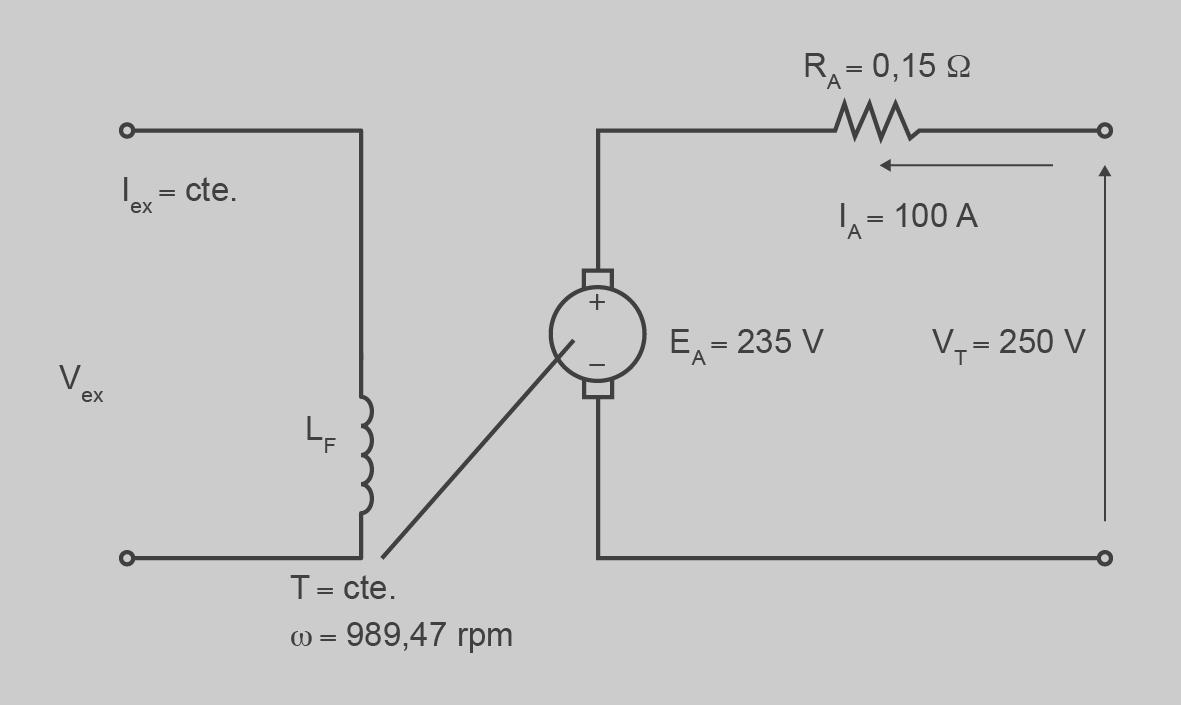
Per tant, hem disminuït la velocitat de 1.200 a 989,47 rpm. En la figura següent podeu veure els nous valors simulats amb el programari PSim:

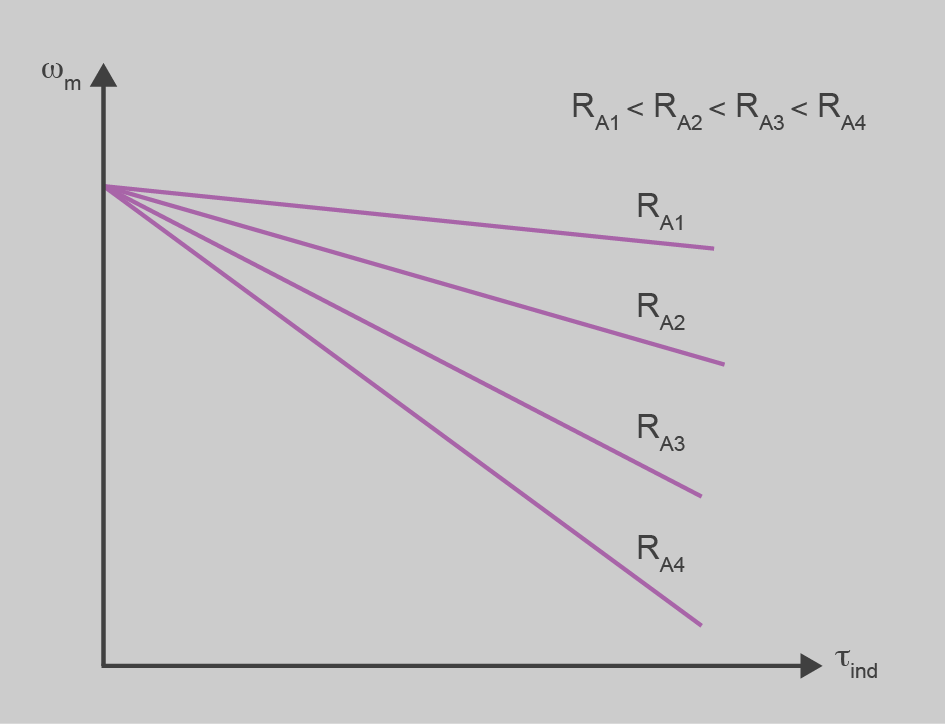
Realment la R_A, la resistència dels bobinatges del rotor, no es pot modificar un cop ja feta la màquina, però sí que es pot posar una resistència en sèrie amb l’induït, i per tant, incrementar el valor de la resistència equivalent.

L’efecte sobre la corba de la velocitat del motor és incrementar el pendent de la corba de la velocitat, mentre que el punt de tall amb l’eix y, que representa la velocitat sense parell de càrrega, o sigui, en buit, no es modifica. La figura mostra aquest efecte.

Atès que tenim tres mètodes per variar la velocitat del motor de CC, interessa saber quan s’utilitza cada un i en quines condicions es pot aplicar. El límit sempre els posen els valors nominals del motor, que no s’han de sobrepassar de manera permanent. Ja que la regulació per increment de R_A només s’ha de fer de manera ocasional o en petites potències, ens limitarem al control per I_ex i V_T.

En el cas de variació de V_T, es modifica la velocitat de la manera següent:

• Si volem incrementar la velocitat (ω↑) s’ha d’incrementar la V_T (V_T↑)
• Si volem decrementar la velocitat (ω↓) s’ha de decrementar la V_T (V_T↓)

En el cas de variació de I_ex, es modifica la velocitat de la manera següent:

• Si volem incrementar la velocitat (ω↑) s’ha de decrementar la I_ex (V_ex↓)
• Si volem decrementar la velocitat, (ω↓) s’ha d’incrementar la I_ex (V_ex↑)

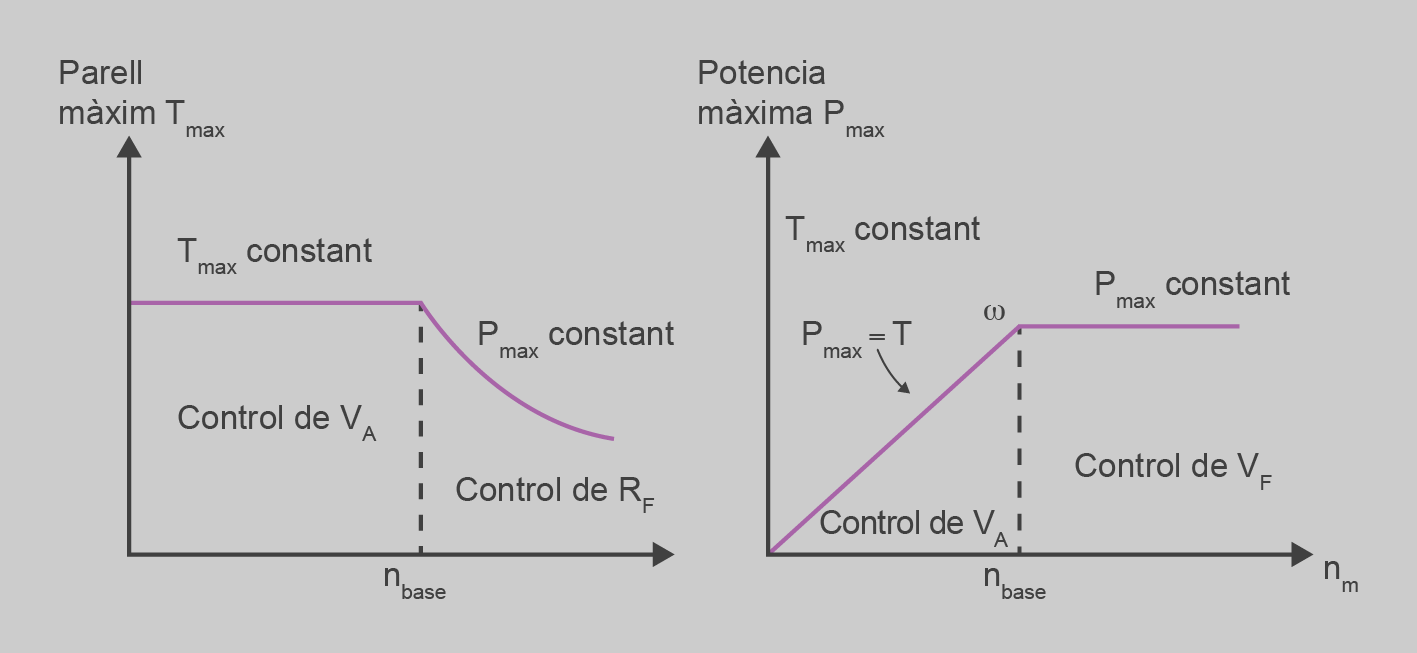
Per a velocitats inferiors a la nominal, regulades amb la V_T, el parell es pot mantenir al seu valor nominal, i com la potència és el producte de la velocitat pel parell, tenim una potència que s’incrementa a mesura que la velocitat s’incrementa.

Per a velocitats superiors a la nominal, regulades amb la I_ex, no es pot mantenint el parell nominal, ja que la potència seria superior a la nominal, i això produiria un sobreescalfament del motor. En canvi, per mantenir la potència constant, el parell s’ha de decrementar a mesura que la velocitat es fa més gran. La figura mostra com han de ser el parell i la potència per a aquestes regulacions.

Fa uns anys, quan encara no es disposaven de components d’electrònica de potència amb les característiques dels actuals, es van idear diversos sistemes per controlar la velocitat dels motors de CC. Un d’aquests, molt versàtil, és el denominat Ward Leonard.

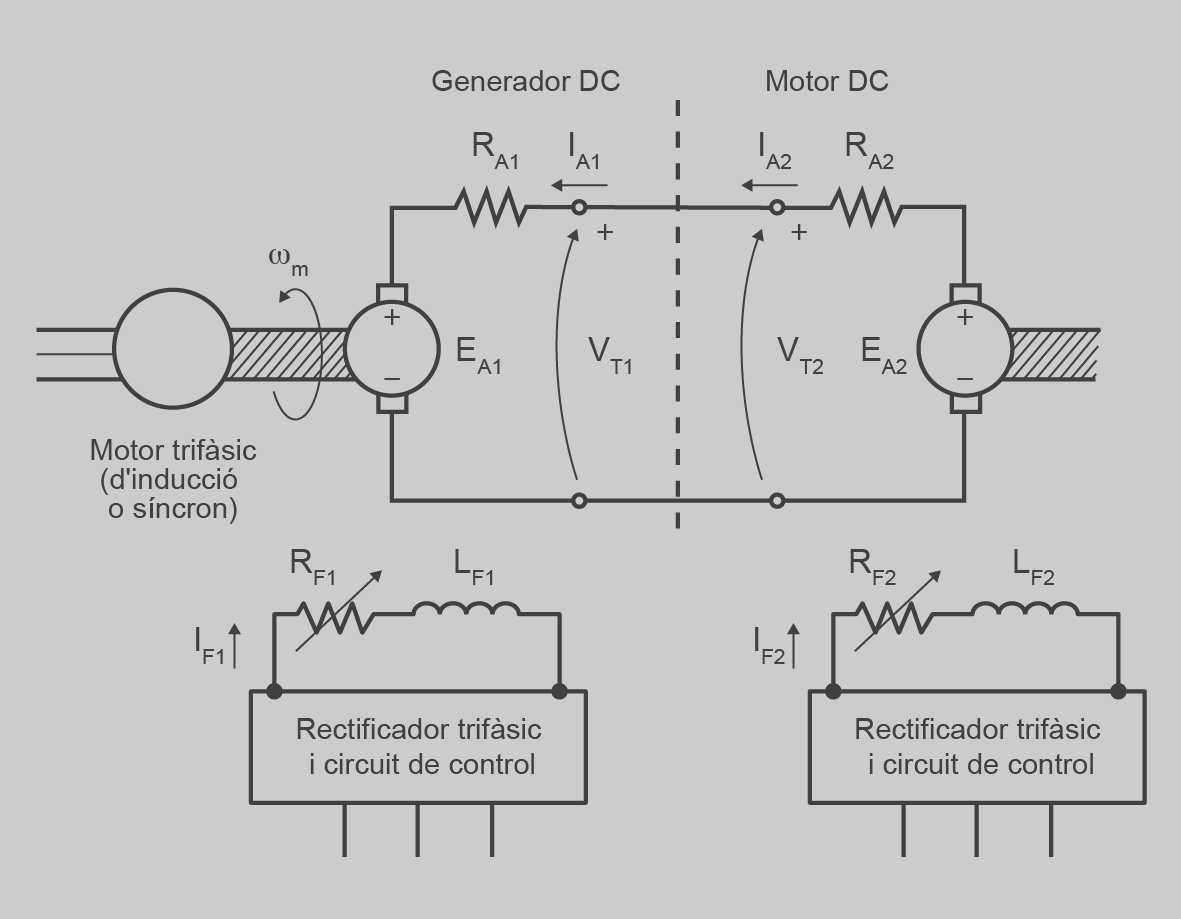
Aquest sistema consisteix en dues màquines de CC d’excitació independent, una treballant com a generador i l’altra com a motor. A la figura podem veure aquesta disposició.

El generador gira mogut per una màquina d’inducció acoblada al mateix eix que la màquina que treballa com a motor. La variació de V_T i, per tant, de la velocitat del motor de CC, s’aconsegueix variant la R_F i la R_F2.

Com la màquina d’inducció varia poc la seva velocitat en variar la càrrega, podem considerar que treballa a velocitat constant i, per tant, la tensió en borns del generador de CC V_T1 = V_T2 depèn del seu corrent d’excitació. Modificant aquest corrent, cosa que podem podem aconseguir variant la R_F1, podem modificar la V_T del motor de CC des de 0 fins a la tensió nominal, i per tant controlar la velocitat.

Amb la variació de R_F2 es pot controlar la velocitat del motor de CC per sobre de la velocitat nominal. O sigui, que amb R_F1 i R_F2 podem controlar la velocitat del motor des de 0 fins a una velocitat superior a la nominal.

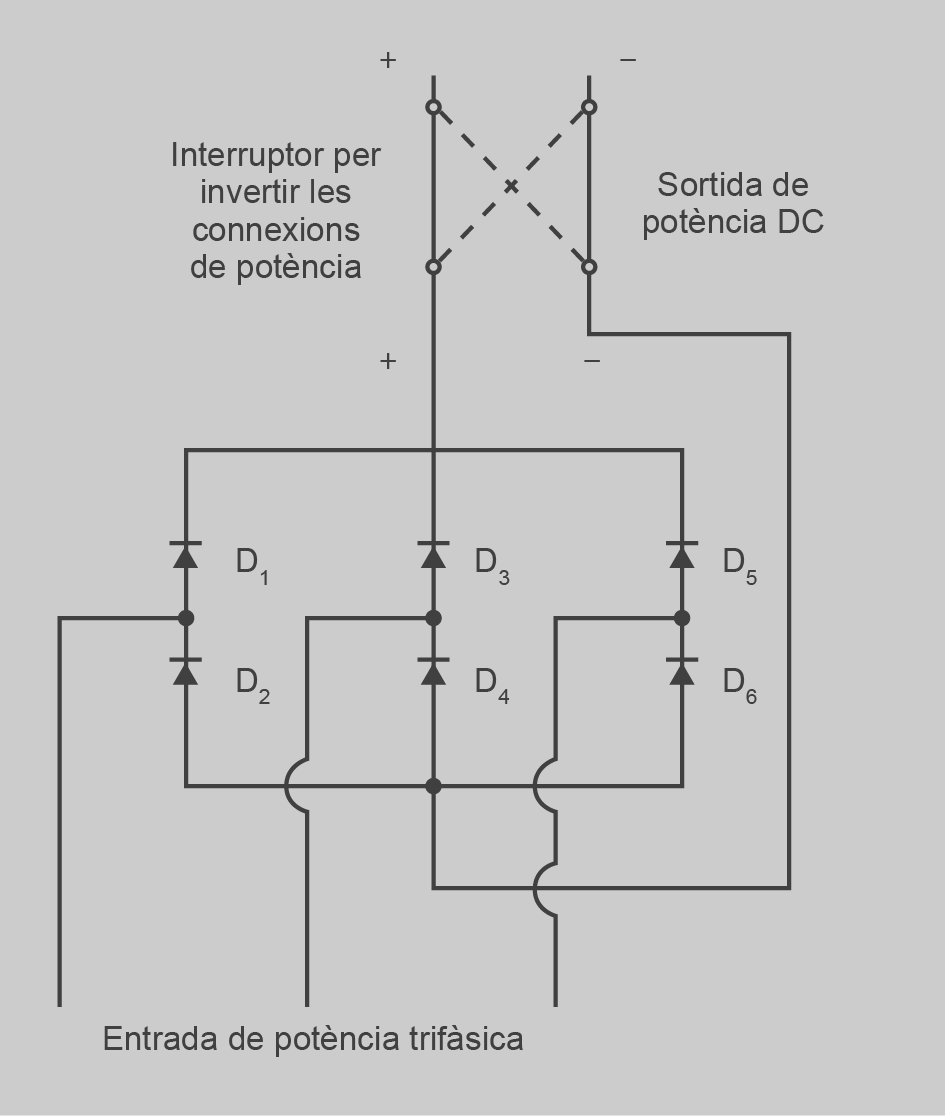
A la figura podeu veure al circuit rectificador per a la tensió dels bobinatges de les màquines de CC. Aquest circuit inclou un contactor que ens permet fer girar la màquina en sentit contrari, invertint el corrent al circuit d’excitació del generador.

Com a resum, es pot dir que el sistema Ward Leonard pot controlar la velocitat del motor de CC des de 0 fins una velocitat superior a la nominal, en totes dues direccions, i que, a més a més, pot retornar energia a la xarxa.

L’inconvenient del sistema és que per aconseguir aquest enorme ventall de control de velocitat cal adquirir tres màquines d’una potència similar:

• Una màquina asíncrona
• Dues de corrent continu

Per tant, és un sistema car i que ocupa molt espai.

Actualment es disposa de components estàtics d’electrònica de potència robusts i fiables, que permeten aconseguir tensions variables de manera més còmoda i econòmica, amb menys espai i soroll i pràcticament lliures de manteniment.

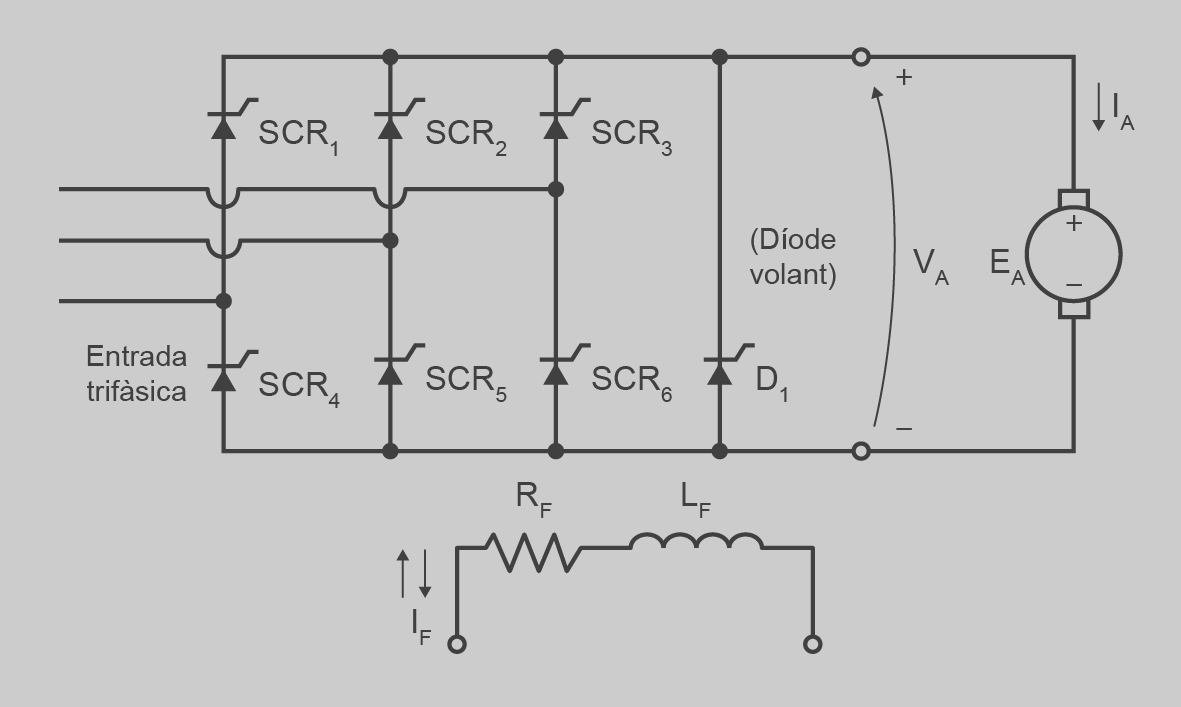
El descobriment del tiristor i les millores posteriors de les seves característiques han permès aquest control. A la figura podem veure un rectificador trifàsic amb 6 tiristors totalment controlat.

Aquests 6 tiristors substitueixen el motor d’inducció i una màquina de CC del sistema Ward Leonard, però no permeten retornar energia a la xarxa. El valor mitjà de la tensió en borns V_A depèn de l’angle de disparament dels tiristors.

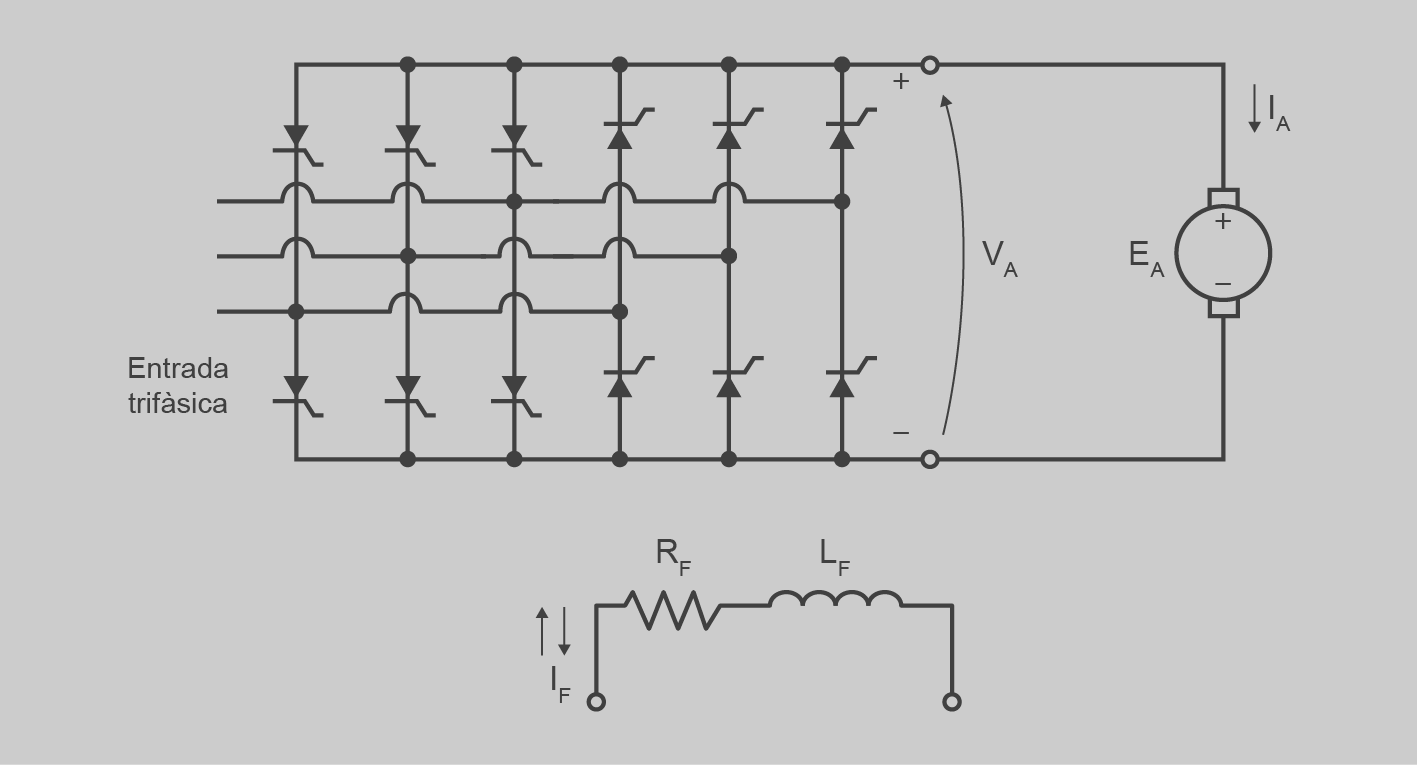
Si es vol un circuit que permeti retornar energia a la xarxa, s’ha de posar un rectificador doble com el que es mostra a la figura.

La figura no inclou el circuit de control dels tiristors, però actualment ja es disposa de circuits integrats que permeten aconseguir aquest control de manera molt fàcil.