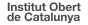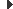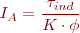Principis de màquines de corrent continu
Totes les màquines estan formades per un conjunt de peces acoblades entre elles amb la finalitat d’efectuar una transformació d’energia. L’estudi de cada una d’aquestes parts i la documentació tècnica que acompanya la màquina és important per tenir-ne una visió global del funcionament.
Elaboració de documentació tècnica de màquines elèctriques rotatives de corrent continu
Com la resta d’elements d’un circuit, la documentació tècnica que inclou màquines de corrent continu s’ha d’ajustar a les normes dictades pels diferents organismes estandarditzadors nacionals i internacionals. Aquesta estandardització de la simbologia ens ha de permetre interpretar els diferents esquemes de maniobres i la potència de màquines elèctriques de CC independentment de la seva procedència.
Simbologia normalitzada i convencionalismes de representació en la reparació de màquines elèctriques rotatives de corrent continu
Per representar les màquines de corrent continu s’utilitzen els símbols normalitzats de la taula. Aquests símbols estan extrets de la norma EN-60617, que especifica els símbols, colors, estructura de la informació, numeració de borns, etc., de la documentació electrotècnica.
| Símbol | Descripció |
|---|---|
 | Motor CC excitació sèrie |
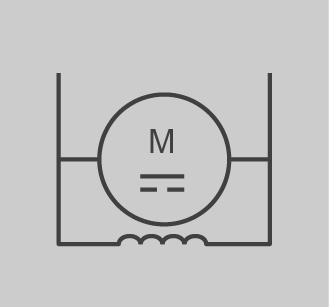 | Motor CC excitació derivació (shunt) |
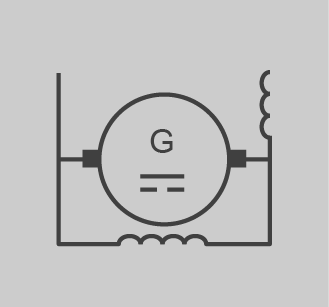 | Generador CC excitació composta curta (amb terminals i escombretes) |
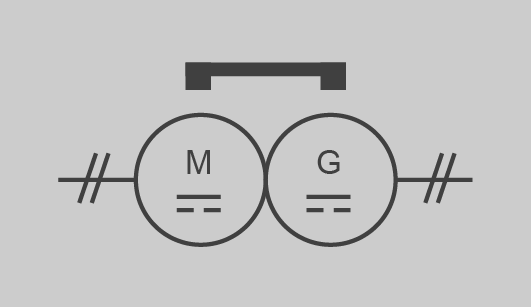 | Convertidor rotatiu CC excitació comú d’imant permanent |
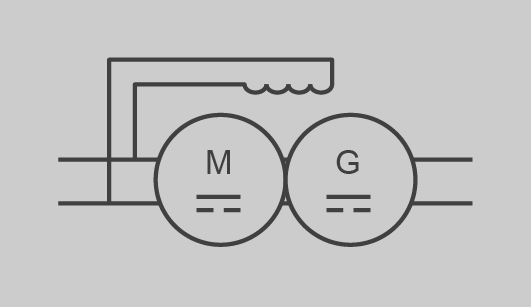 | Convertidor rotatiu CC debanat d’excitació comú |
Esquemes de màquines de corrent continu
En els circuits on treballen màquines de CC hi sol haver els circuits següents:
- El circuit de maniobra, amb les bobines, relés i contactors
- El circuit de potència, amb el motor i els contactes dels relés del circuit de maniobra.
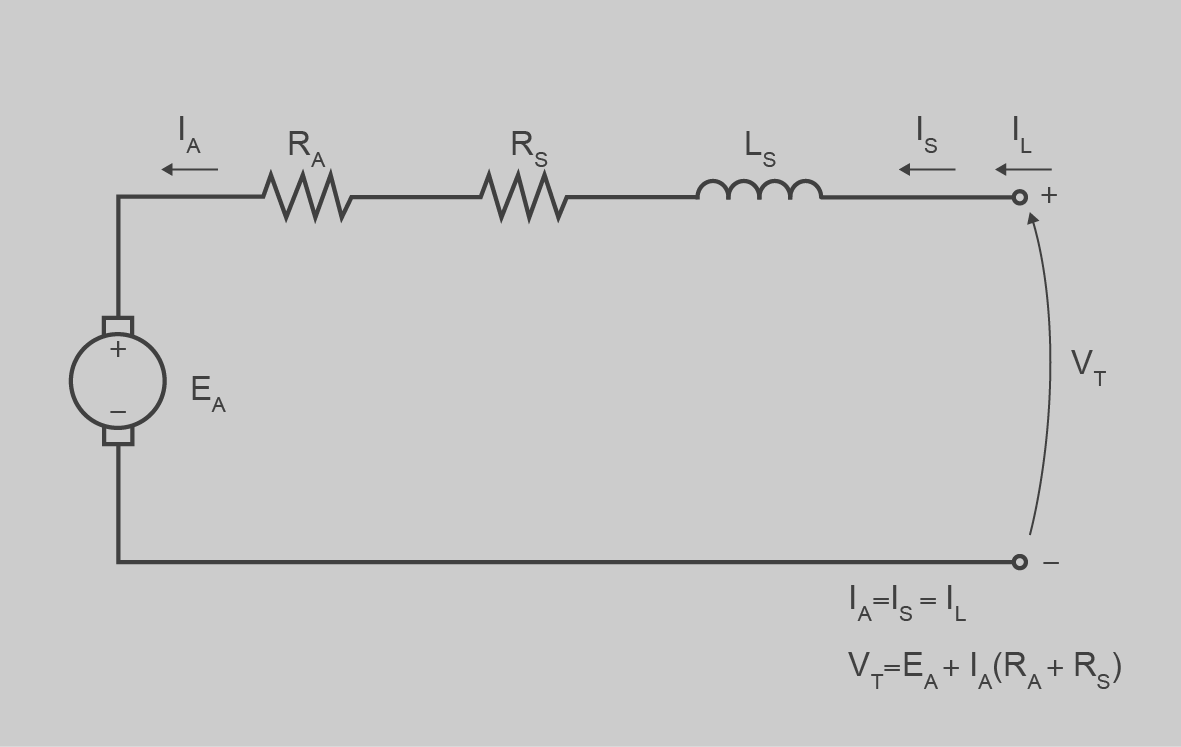
Tots dos solen estar protegits contra sobreintensitats, sobreescalfament i corrents diferencials residuals. En la figura podeu veure un circuit típic associat a un motor de CC.
Aplicació de programari informàtic de dibuix tècnic i càlcul d’instal·lacions
Es poden trobar una gran varietat de programes per a la representació d’esquemes amb màquines de corrent continu i el càlcul de magnituds elèctriques i mecàniques. En general els podem dividir en programes de propietat i lliures.
Els programaris de propietat són aquells que pertanyen a una empresa determinada que cobra per utilitzar-lo, i l’usuari no pot accedir al codi per modificar-lo.
El programari lliure és aquell en què el seu creador publica el codi i les biblioteques perquè es puguin utilitzar i modificar. A més a més, en la majoria de casos sol ser gratuït.
Entre els programaris de propietat, un dels més utilitzats per a representació gràfica és l’Autocad, que, utilitzant una biblioteca elèctrica, permet fer tot tipus d’esquemes elèctrics amb grans prestacions. És un programa de propòsit general que es pot aplicar a esquemes elèctrics.
Elcad és un altre programa de propietat especialitzat en la representació d’esquemes elèctrics utilitzat a escala industrial per moltes empreses del sector, amb grans prestacions i una bona biblioteca de material elèctric i electropneumàtic.
Actualment tots els càlculs amb màquines elèctriques se solen fer paral·lelament de manera analítica i amb el suport d’un programa d’elements finits que simuli el circuit.
Tant el Pspice o la seva versió de demostració Design Lab eval 8 permeten la simulació de màquines elèctriques, però utilitzar-lo és difícil: cal conèixer detalls de la màquina que es poden mesurar o induir a escala acadèmica, però de què normalment no es disposa a escala industrial.
Per al càlcul de màquines elèctriques es pot trobar programari lliure de bona qualitat.
Entre el programari lliure podem destacar el Psim, que permet simular màquines elèctriques en general, inclosa l’etapa transitòria.
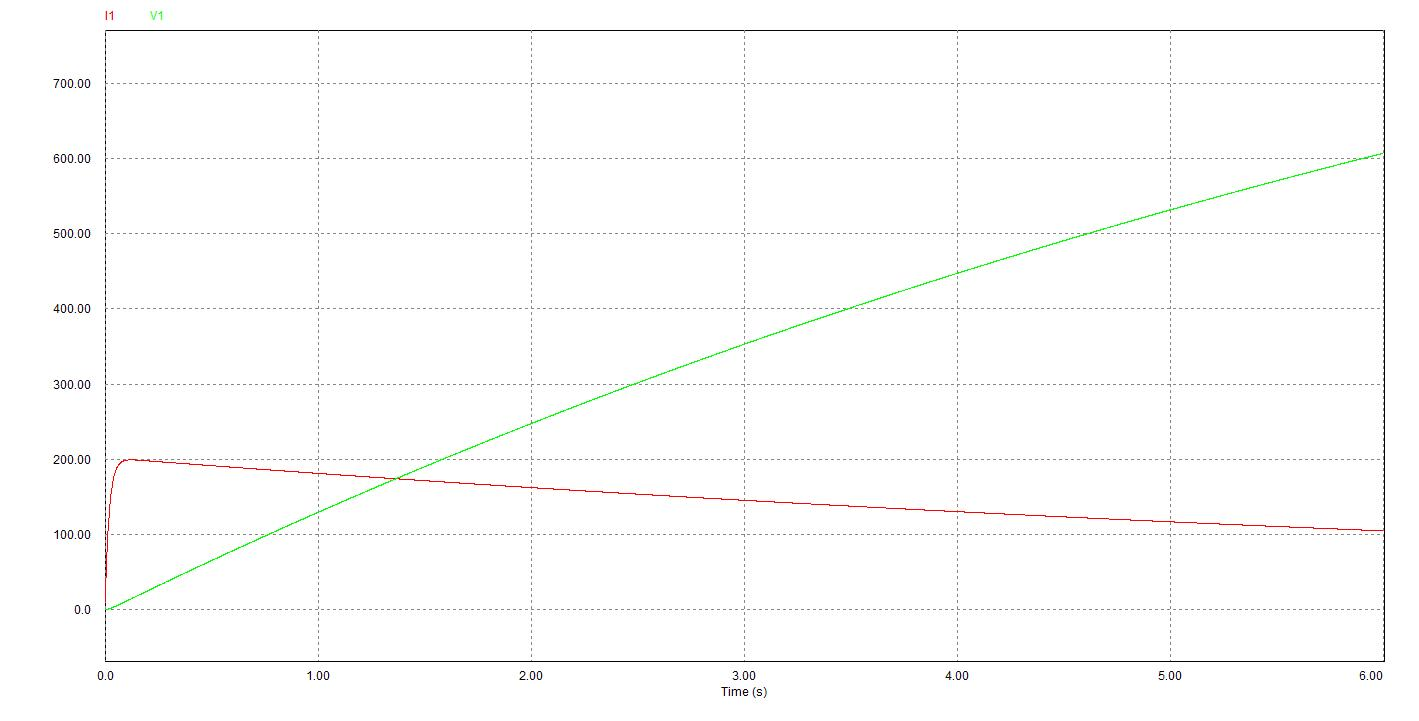
Com a exemple d’ utilització del programa Psim podeu veure a la figura una simulació d’un motor de corrent continu amb una càrrega mecànica i el resultat de la simulació.
A la màquina de corrent continu del Psim es poden parametritzar les variables següents:
 (armature). Resistència d’armadura, en ohms
(armature). Resistència d’armadura, en ohms  (armature). Inductància d’armadura, en H
(armature). Inductància d’armadura, en H  (field). Resistència de camp, en ohms
(field). Resistència de camp, en ohms  (field). Inductància de camp, en H
(field). Inductància de camp, en H - Moment of inertia. Moment d’inèrcia J, en kg·m·m
 (rated). Voltatge nominal, en V
(rated). Voltatge nominal, en V  (rated). Corrent nominal, en A
(rated). Corrent nominal, en A - n (rated). Velocitat nominal, en rpm
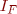 (rated). Corrent nominal de camp, en A
(rated). Corrent nominal de camp, en A - Torque flag. Indicador de sortida del parell (0 o 1)
Les equacions que descriuen el funcionament són les següents:
en què:
- VT = voltatge en bornes de l’induit
- VF = voltatge en bornes de l’inductor
- EA = força contraelectromotriu del rotor
- IA = corrent del rotor
- IF = corrent de camp
- ωm = velocitat mecànica, en rad/s
- LAF = inductància mútua entre bobinatges de camp i del rotor
- τem = Parell motor
- τload = Parell a la càrrega
Observeu que el fet d’usar equacions diferencials és per obtenir la resposta transitòria de les magnituds que es volen mesurar. O sigui, que podem saber com varia la velocitat, la tensió o la intensitat en funció del temps. Per conèixer el valor final, cal fer la simulació durant un període de temps llarg per deixar que el sistema arribi a un valor estabilitzat.
Es poden parametritzar els valors següents de la càrrega mecànica:
- Tc. Parell, en N·m
- K1 (coefficient). Coeficient per al terme lineal
- K2 (coefficient). Coeficient per al terme quadràtic
- K3 (coefficient). Coeficient per al terme cúbic
- Moment of inertia. Moment d’inèrcia J, en kg·m·m
Una càrrega mecànica resistiva es pot expressar com:

en què:
 = velocitat mecànica en rad/s
= velocitat mecànica en rad/s- sign(ω) = signe de la velocitat mecànica
Triant correctament els coeficients de la càrrega es poden modelitzar diversos tipus de càrregues reals com:
- Transportadors:

- Ventiladors i compressors:

A la figura podeu veure el resultat de la simulació, en la qual hem mesurat la intensitat d’entrada al motor (A1) i la velocitat de sortida amb un sensor de velocitat que transforma la velocitat en tensió (V1).
Generalitats, topologia i constitució de màquines de CC
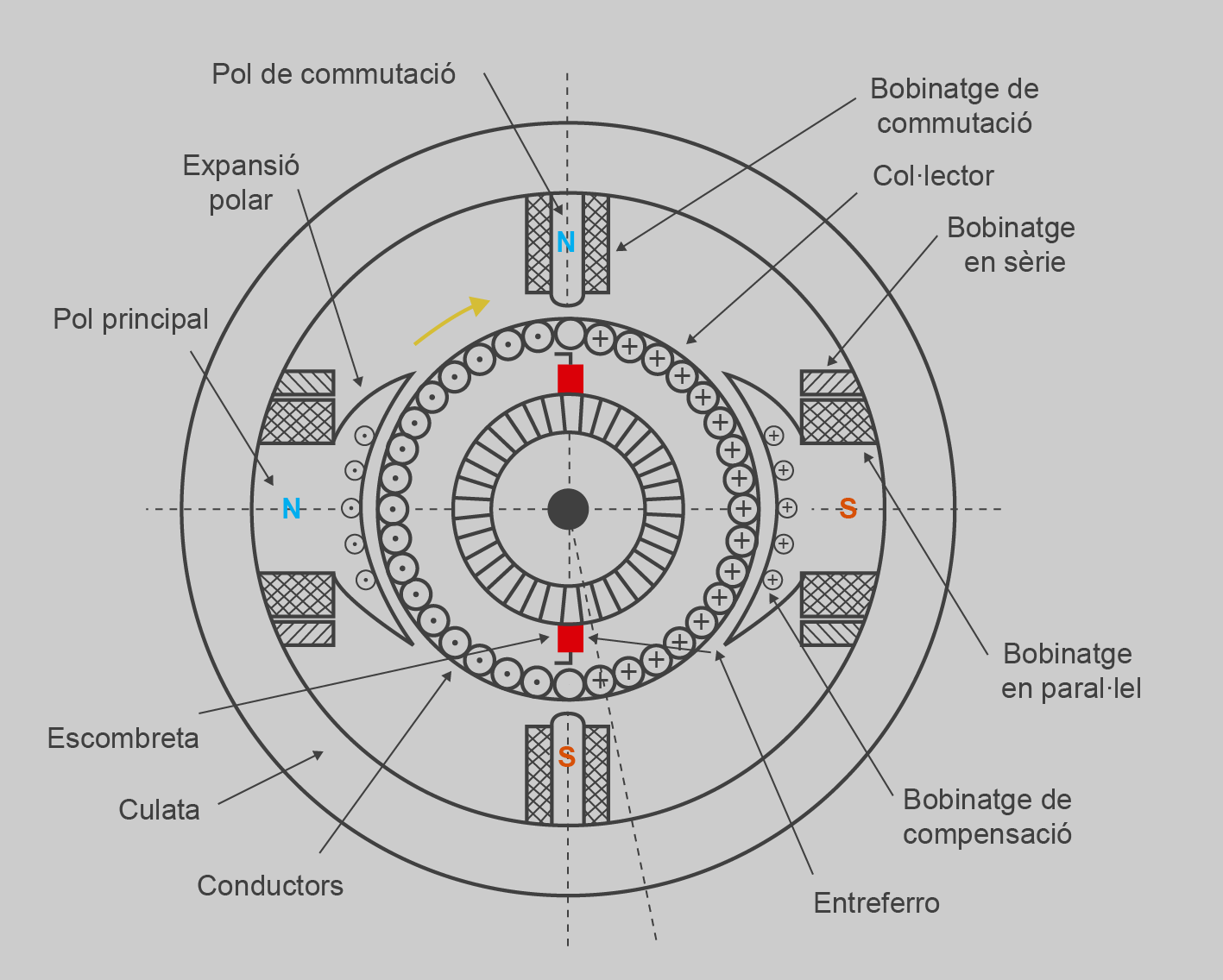
Com totes les màquines giratòries, la màquina de CC està constituïda per una part fixa, denominada pel seu nom mecànic, estator, o pel nom elèctric, inductor i una part que gira, el rotor, també denominat induït o armadura.
A la màquina de CC podem trobar dos circuits elèctrics, situats a l’estator i al rotor (algunes màquines en tenen un tercer, el de commutació) i un circuit magnètic, a més de dielèctrics i parts mecàniques, i altres parts que proveeixen ventilació, nanses per al transport, etc.
Circuits elèctrics i magnètics
-

- Estator bobinat d'una màquina de CC (imatge: Barbour a http:goo.glc0WJc)
Els materials elèctrics (bobines de coure) i magnètics (xapes magnètiques), formen la part essencial de la màquina de CC, però necessiten suports, fixacions, ventilació, rodaments, etc., que els permetin fer la seva funció. La figura mostra les parts essencials de la màquina. Els bobinatges d’excitació, situats sobre els pols principals, generen un camp magnètic que és simètric respecte a la línia que passa pel centre dels dos pols. Aquesta línia s’anomena eix de camp o eix directe. L’eix perpendicular a l’eix de camp és l’eix de quadratura.
-

- Rotor bobinat d'una màquina de CC (imatge cortesia de http:www.aulaelectrica.es)
A la figura es pot apreciar un detall esquemàtic dels pols d’una màquina de CC.
Des del punt de vista mecànic, podem distingir dues parts ben diferenciades a la màquina de CC:
- Estator, que es la part estàtica de la màquina.
- Rotor, que es la part de la màquina que gira.
En una màquina de CC podem distingir diversos circuits. Els més importants son el circuit elèctric i el magnèti, formats per les següents parts:
- Culata, que és la peça base a la quan van subjectes la resta de peces de la màquina (apreciable en la figura). Com el flux és aproximadament constant, sol estar feta de ferro dolç.
- Pols principals, on estan situades les bobines d’excitació, que són les que generen el flux de l’estator de la màquina (figura).
- Entreferro, que és l’espai entre l’estator i el rotor. Ha de ser el més petit possible, però suficientment gran per permetre que el rotor giri sense tocar l’estator, tenint en compte les toleràncies de fabricació i el desgast dels coixinets (apreciable a la figura).
- Nucli rotòric, que és el cilindre de xapes magnètiques subjectat a l’eix on se situa el bobinatge rotòric. En girar, està sotmès a un camp magnètic variable, i per tant, ha de ser de xapa magnètica per reduir les pèrdues de Foucault (figura). Al nucli rotòric va collat el rotor i el col·lector de delgues, al qual van connectades les delgues del col·lector (figura).
- Bobinatge inductor, constituït per tantes bobines com pols principals té la màquina. La seva funció és crear un camp magnètic dintre de la màquina que concateni les bobines del rotor i s’hi generi força electromotriu en girar. La polaritat és tal que estan alternats pols oposats, un de nord i un de sud. Algunes màquines petites tenen imants permanents en lloc d’electroimants a l’estator.
- Pols i bobinatges de commutació i de compensació, situats a l’estator. A l’estator hi ha, intercalats amb els pols principals, uns altres pols que generen un camp magnètic per millorar el funcionament de la màquina: són els pols de commutació, sobre els quals es bobina un debanatge auxiliar que serveix per millorar la commutació de la màquina; es connecten en sèrie amb el circuit inductor amb polaritat igual que el pol anterior en el sentit de gir de la màquina. El bobinatge de compensació esta situat a l’extrem dels pols principals i serveix per compensar el flux magnètic creat per bobinatge del rotor de la màquina.
- Escombretes, que son peces de carbó que serveixen per introduir el corrent elèctric als bobinatges del rotor. Penseu que s’ han de fer passar corrent elèctric pels bobinatges del rotor, que giren contínuament. Les escombretes fixades sobre la culata,freguen sobre el col·lector de delgues situat al rotor. D’aquesta manera s’aconsegueix un contacte elèctric constant entre la part fixa i la que gira de la màquina.
- Col·lector de delgues, que esta situat en el rotor de la màquina. Sobre ell freguen les escombretes que li entreguen el corrent elèctric per alimentar el bobinatge del rotor.
Placa de borns d’una màquina de CC
Els bobinatges de la màquina de CC tenen els terminals a la placa de connexions, on es connecten els bobinatges entre ells i a l’alimentació del motor. La taula indica els noms normalitzats dels bobinatges.
| Bobinatge | Denominació antiga | Denominació nova |
|---|---|---|
| Induït | A-B | A1-A2 |
| Inductor en paral·lel | C-D | E1-E2 |
| Inductor en sèrie | E-F | D1-D2 |
| Inductor independent | J-K | F1-F2 |
| Inductor de commutació | G-H | B1-B2 |
Valors característics de les màquines de CC
A la placa de característiques d’una màquina de CC hi podeu trobar tots els valor per als quals la màquina ha estat construïda.
Cavalls i watts
En moltes màquines es dóna la potència mecànica en CV (cavalls de vapor). És una mesura anglesa i la seva equivalència al sistema internacional és de 1 CV = 736 W.
Els valors informats en la placa de característiques d’una màquina no s’han de sobrepassar en el funcionament habitual de la màquina.
A la figura podeu observar una placa de característiques d’un motor de la marca ABB, molt completa, on, a més de les seves característiques elèctriques, podeu veure detalls del manteniment o de refrigeració.
Corbes característiques de les màquines elèctriques rotatives de corrent continu
Les corbes característiques mostren el funcionament de les màquines elèctriques. Com hi tenim energia elèctrica i mecànica, hi podem trobar relacions entre corrents, tensions, parells i velocitats. Les relacions entre aquestes no sempre són lineals, i per facilitar la interpretació, en lloc d’equacions s’usen preferentment mètodes gràfics, o sigui, corbes característiques per explicar el funcionament de les màquines elèctriques.
No obstant això, conèixer les equacions que relacionen les variables elèctriques i mecàniques proporciona un mètode molt potent per explicar el funcionament de la màquina sempre que suposem que treballa en zona lineal.
Les equacions que ens permeten explicar el funcionament de la màquina i que expliquen la forma de les corbes característiques són:
- Primera llei de Kirchhoff:

- Segona llei de Kirchhoff:



Les equacions de Kirchhoff relacionen tensions i corrents al dispositiu. La segona equació relaciona la tensió que es genera al bobinatge del rotor del motor amb el flux de la màquina i la velocitat a la qual gira, i la tercera relaciona el parell que genera el motor amb el flux i la intensitat que passa pel rotor del motor.
Els bobinatges inductor (estator) i induït (rotor) es poden connectar independentment cadascun a una font de tensió, però també es poden connectar a la mateixa font de tensió en sèrie o en paral·lel. En cada cas tenim una màquina de característiques diferents.
Excitació independent i excitació en paral·lel
Els motors de CC permeten un gran marge de variació de velocitat de manera molt simple. Això els ha popularitzat molt en gran varietat d’aplicacions.
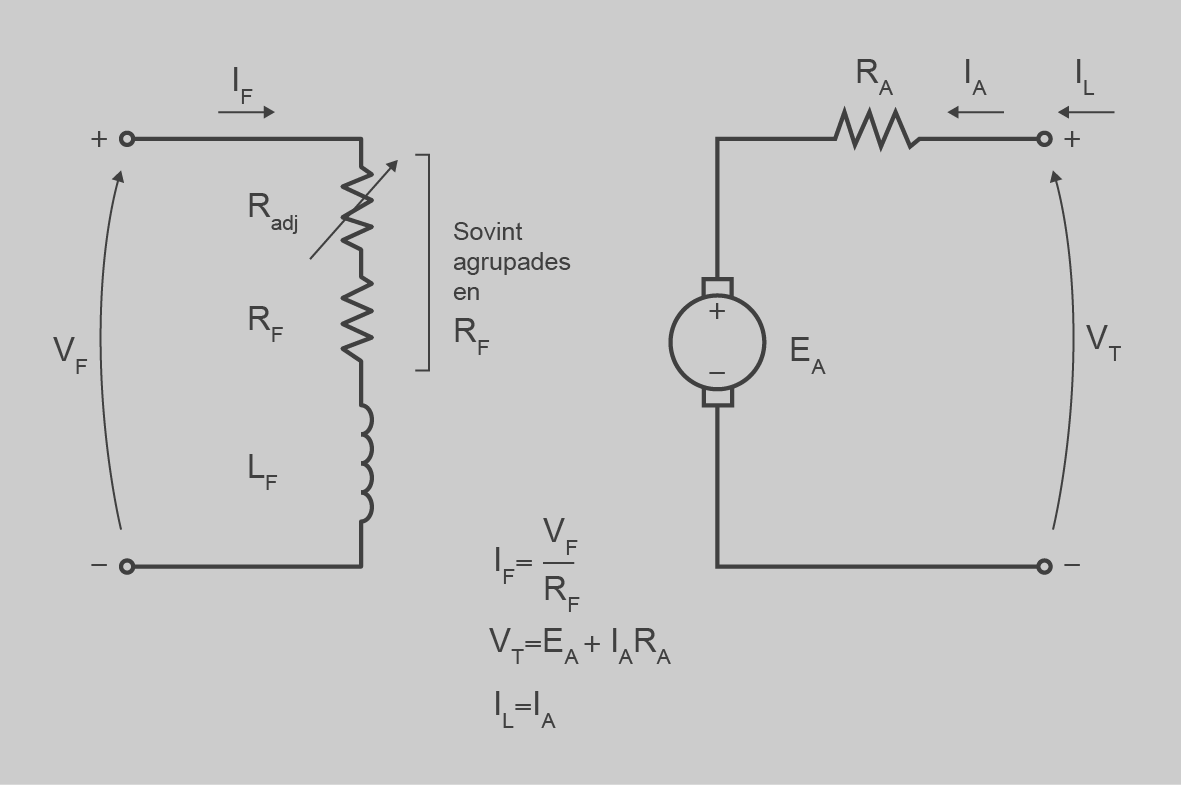
En el cas d’excitació independent hi ha dues fonts de tensió, una per a l’inductor i una per a l’induït. Es poden variar de manera independent i permet una gran varietat de regulació (figura).
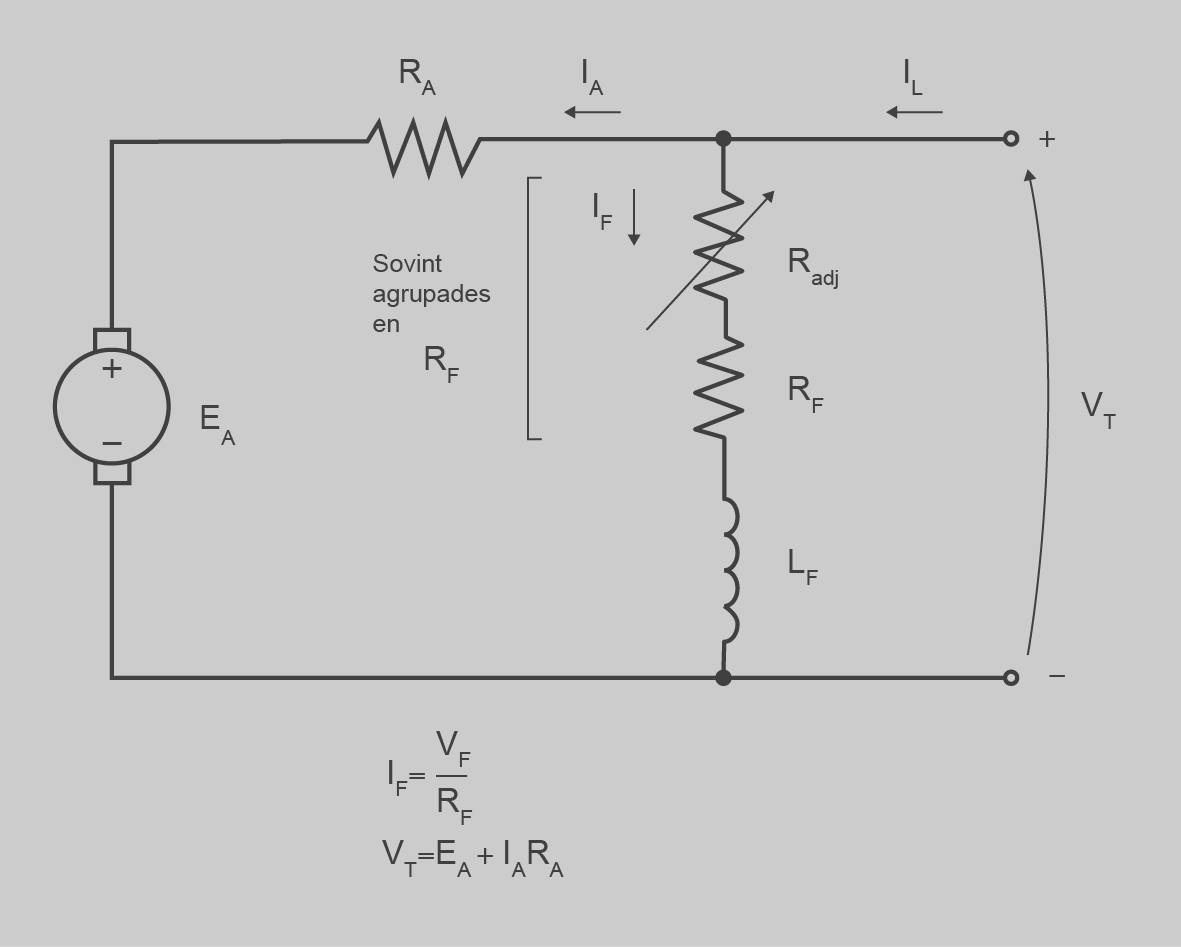
En el cas d’excitació en paral·lel es connecten inductor i induït a la mateixa font de tensió. Les equacions són les mateixes, però queda restringit al cas que la tensió nominal de tots dos bobinatges és la mateixa (figura).
Les connexions de la màquina de corrent continu independent i en paral·lel tenen un comportament similar i es poden analitzar de manera conjunta.
A partir de l’esquema del circuit equivalent podem trobar les equacions del motor:
en què:
- VT = tensió a la qual connectem la màquina
- K = constant de la màquina
 = flux magnètic dintre de la màquina
= flux magnètic dintre de la màquina- RA = resistència del bobinatge induït
- τind = parell induït
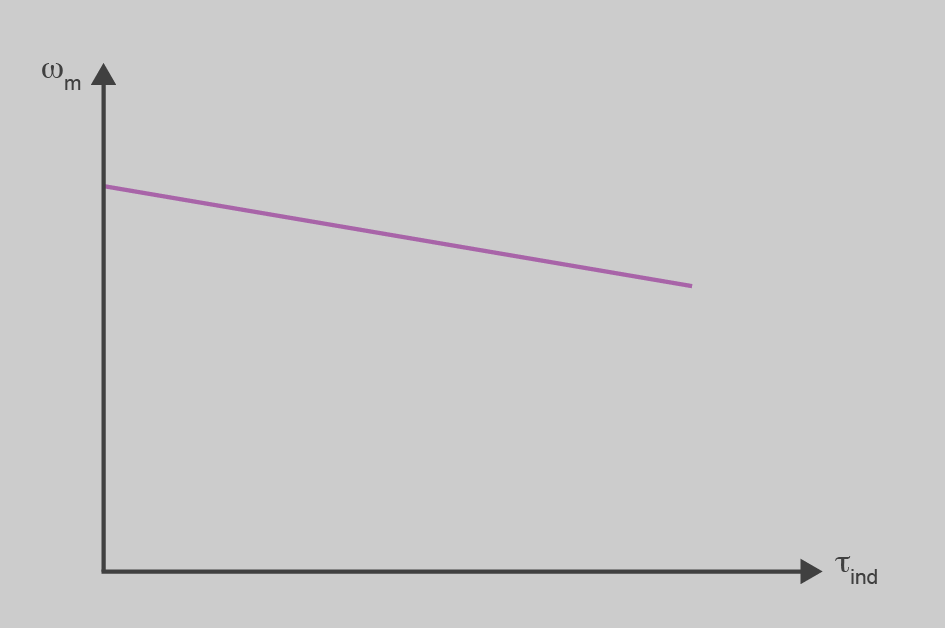
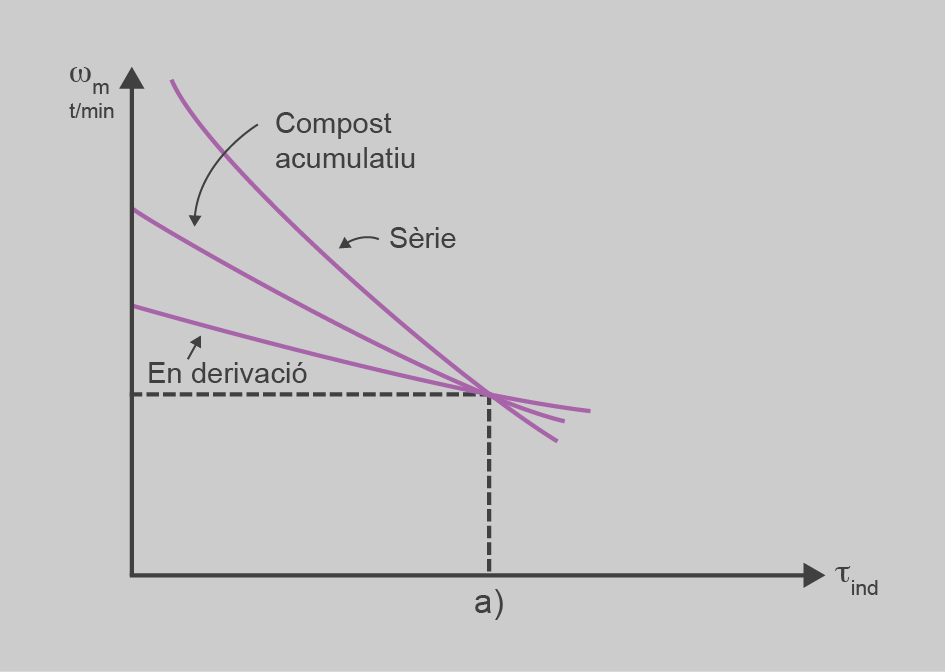
Per a una màquina ja construïda, les magnituds K i RA són constants de la màquina, que ja no les podem modificar, i per tant, podem dir que si mantenim constant la VT, a mesura que s’incrementa el parell resistent la velocitat del motor disminueix. A la figura podeu veure aquest efecte.
La caiguda de velocitat no és gaire pronunciada, i per tant el motor de corrent continu d’excitació en paral·lel s’utilitzarà en aquelles aplicacions que requereixin poca variació de velocitat encara que variï la càrrega.
Excitació en sèrie
En els motors d’excitació en sèrie els dos bobinatges en connecten en sèrie i hi passa el mateix corrent (figura). El bobinatge d’excitació és de poques espires i del mateix gruix.
En aquest cas, si suposem que la relació entre la intensitat i el flux és constant, o sigui, que la màquina no treballa saturada, s’obté l’expressió per a la velocitat del motor següent:
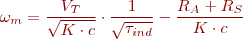
en què:
- ω = velocitat angular, en rad/s
- VT = tensió a la qual connectem la màquina
- K = constant de la màquina
 = flux magnètic dins la màquina
= flux magnètic dins la màquina- RA = resistència del bobinatge induït
- Rs = resistència del bobinatge inductor
- τind = parell induït
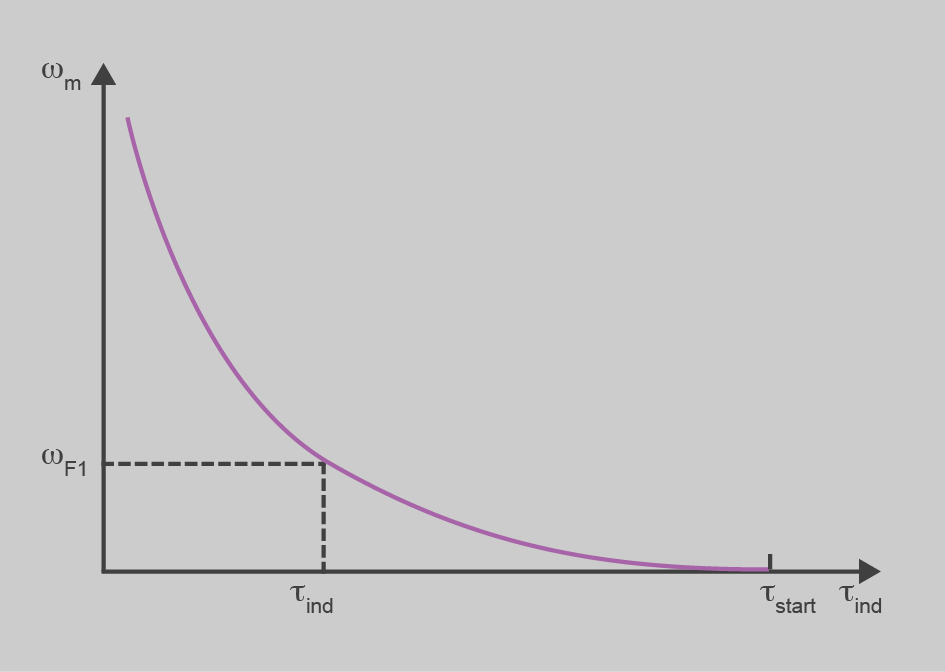
En aquest cas podem veure com la velocitat del motor depèn inversament de l’arrel quadrada del parell motor. És una relació complexa que es pot grafiar com es mostra en la figura.
Un motor de CC d’excitació en sèrie no s’ha de quedar mai sense corrent al bobinatge d’excitació. Si això passes, la velocitat i el corrent del rotor s’incrementarien fins que saltessin les proteccions del motor o fins a la seva destrucció.
Com podeu observar, en els motors de corrent continu d’excitació en sèrie hi ha una forta caiguda de velocitat a mesura que s’incrementa el parell de la càrrega, però el producte del parell per la velocitat roman pràcticament constant. O sigui, que la potència consumida no varia amb la càrrega. Això els fa especialment atractius en aplicacions de sistemes de transport, ja que la potència que transporta la línia d’alimentació és pràcticament constant.
El motor d’excitació en sèrie no pot quedar en buit (sense càrrega), perquè la velocitat s’incrementa excessivament. Per tant, en totes aquelles aplicacions en què la transmissió de potència es faci amb corretges o un altre sistema que es pugui trencar fàcilment, s’ha de tenir cura de protegir el motor.
Excitació composta
En una màquina d’excitació composta hi ha els dos tipus de bobinatges a l’inductor: un per connectar-lo en sèrie amb l’induït i un altre per connectar-lo en paral·lel.
Cadascun té les característiques dels bobinatges en sèrie i en derivació, respectivament.
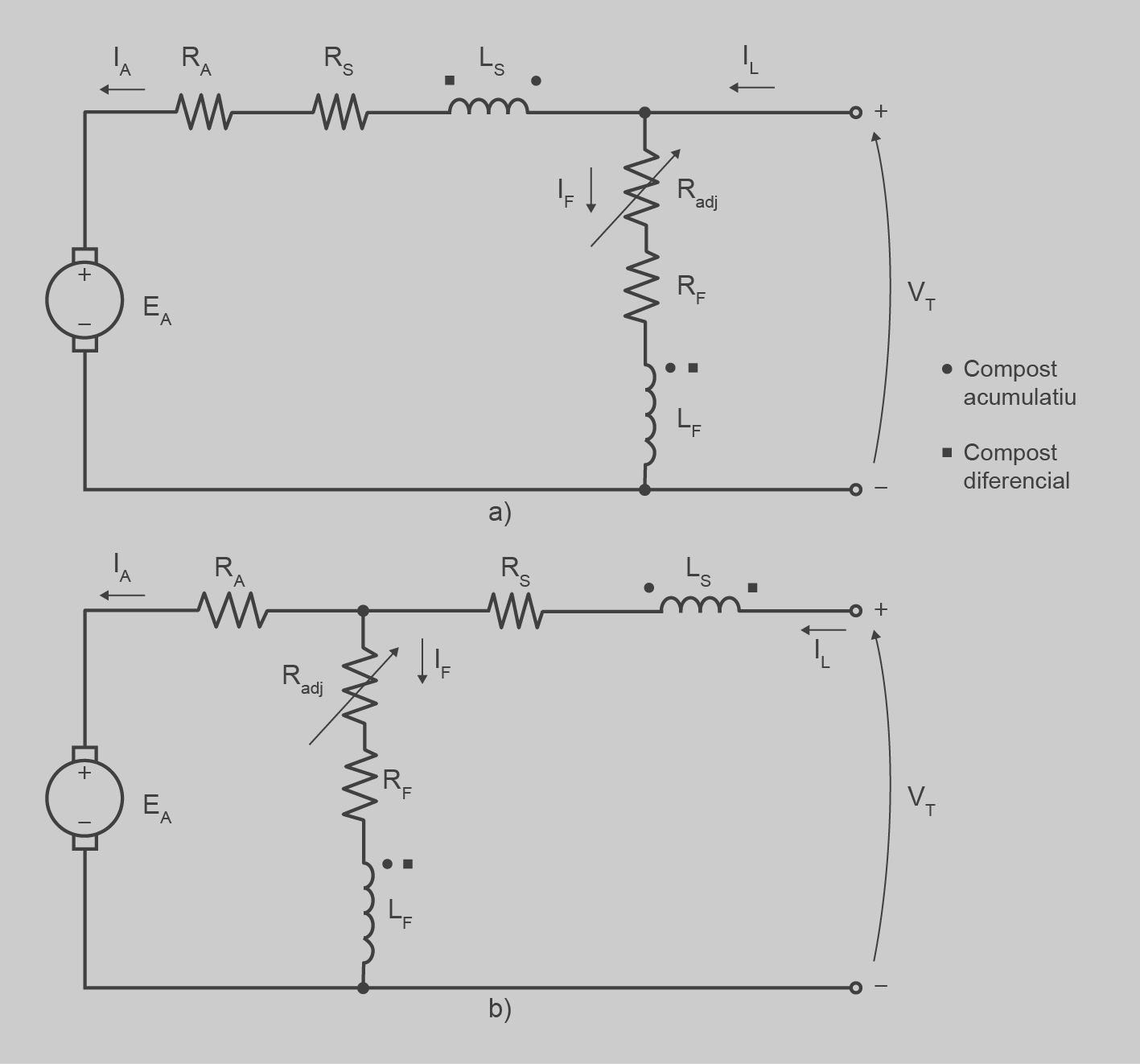
A la figura podem veure dues possibles variacions del motor d’excitació composta de CC. La primera es diu excitació composta de connexió llarga, i la segona, de connexió curta. El funcionament en tots dos casos és molt similar. Els bobinatges s’han de posar de manera que els camps magnètics de tots dos vagin en el mateix sentit i, per tant, se sumin. Es diu excitació composta acumulativa.
Excitació composta
Un motor d’excitació composta té unes característiques mitjanes entre les d’excitació en sèrie i en paral·lel. No s’embala sense càrrega i té un bon parell d’arrencada.
La figura mostra la corba parell-velocitat del motor d’excitació composta comparada amb les d’excitació en sèrie i en paral·lel, en què podem observar que el comportament és una mitjana de totes dues. Té un parell d’arrencada més gran que la d’excitació en paral·lel i no s’incrementa tant la velocitat sense càrrega com en el motor en sèrie.
Bobinatges d’induït
-

- Rotor amb ranures i col·lector de delgues
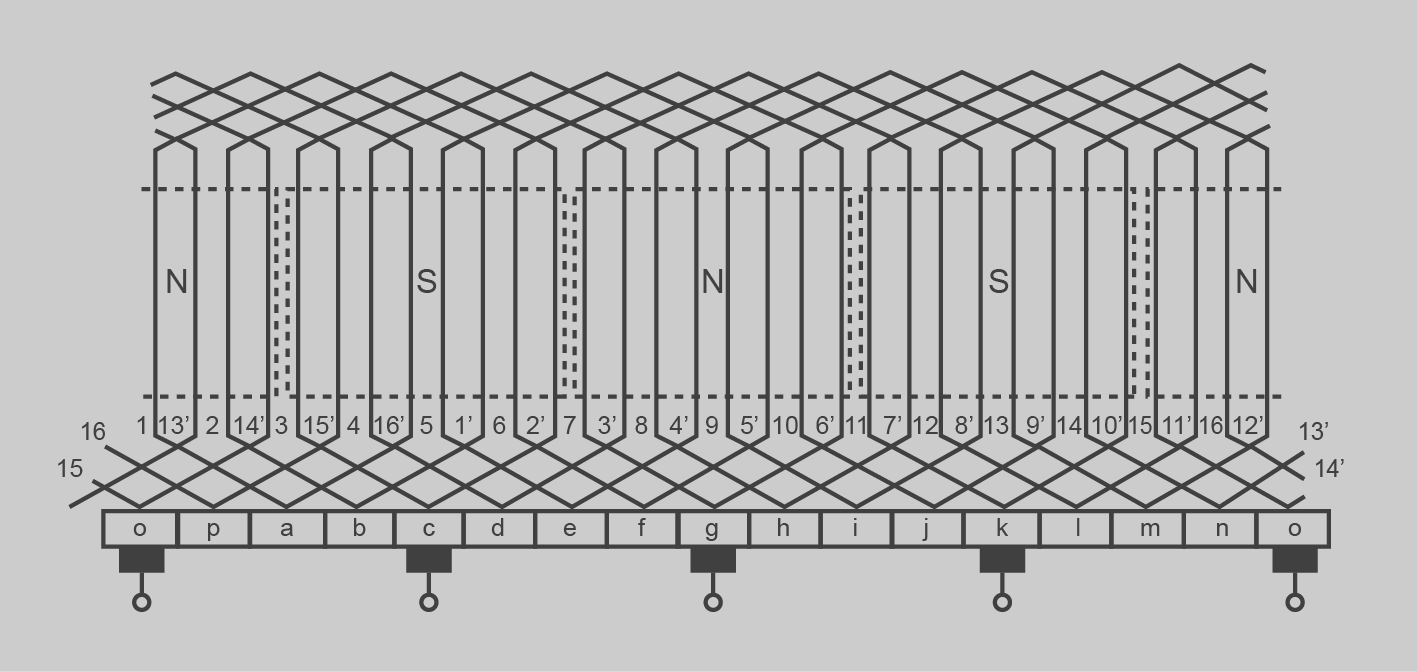
El rotor d’una màquina de CC és un cilindre format per xapes magnètiques apilades i aïllades. A la superfície s’han encunyat unes ranures en les quals s’introdueix el bobinatge de l’induït.
Pràcticament tots els bobinatges són de doble capa. Això vol dir que a cada ranura hi ha un costat d’una bobina i a sota el costat d’una altra (bobinatges imbricats).
En la figura podeu veure, de manera esquemàtica, el bobinatge de doble capa.
Un costat de la bobina entra per una ranura i surt per una altra ranura. La primera condició que ha de complir un bobinatge és que l’amplada de la bobina ha de ser igual que l’amplada polar o molt semblant, perquè la tensió induïda a cada costat de la bobina sigui del mateix valor, però de sentit contrari en passar sota pols diferents. Una bobina pot estar formada per una sola volta de fil o espira o per moltes voltes de fil, però sempre té un inici i un final que van soldats a les delgues del col·lector. Els bobinatges de màquines de CC queden tancats sobre ells mateixos, sense connexions a l’exterior.
Representació gràfica de bobinatges
Els bobinatges estan situats a la perifèria del rotor i, per tant, tenen una distribució cilíndrica. Per representar-los en dues dimensions es fa com si es tingués un paper imaginari a la superfície del cilindre, s’hi fes un tall longitudinal i es desplegués fins a tenir-lo pla. D’alguna manera es tractaria de posar plana la superfície corbada del cilindre (eliminant els cercles de les bases) format per les plaques de fora del rotor i les delgues del col·lector, obtenint un rectangle pla, amb les delgues del col·lector a baix, mostrant-hi les connexions dels successius debanats i la seva imbricació, si n’hi ha.
Passos de bobinatge
Per definir un bobinatge cal indicar el nombre de bobines que el formaran i on anirà col·locada cada bobina dintre les ranures de l’estator, és a dir, a quina ranura se situarà el costat d’anada i a quina altra el de tornada de cada bobina. Per això es defineixen els passos de bobinatge.
Nombre de bobines
Com cada bobina té dos costats i a cada ranura també hi ha un costat d’anada i un de tornada (bobinatge de doble capa) tenim que:

en què:
- B = nombre de bobines
- k = nombre de ranures
En algunes màquines es posen diversos costats de bobina per ranura i capa. Si aquest nombre és u, tenim que:

A la figura hi ha l’esquema d’una ranura amb u = 2.
Com cada bobina té el seu origen en una delga i el seu final en una altra delga del col·lector i, mitjançant les diferents delgues, estan connectades en sèrie formant un circuit tancat, s’ha de complir que:

en què:
- C = nombre de delgues del col·lector
El que diferencia un bobinatge d’un altre és la manera com es connecten les bobines entre si per formar el circuit tancat. Exceptuant les màquines més petites que tenen un parell de pols, la majoria tenen 3, 4 o més parells de pols.
Si tenim més d’un parell de pols, les bobines es poden connectar retrocedint, per connectar en sèrie bobines situades sota el mateix parell de pols (bobinatges imbricats) o avançant per connectar en sèrie bobines situades sota parells de pols diferents, però en posicions similars (bobinatges ondulats).
Tots dos tipus de bobinatges han de ser tancats i s’ha de generar la major tensió possible. Per definir-ne la col·locació a les ranures del col·lector s’han definit els passos de bobinatge. Aquests passos de bobinatge estan comptats en costats actius de bobina, és a dir, el nombre de conductors de la capa superior.
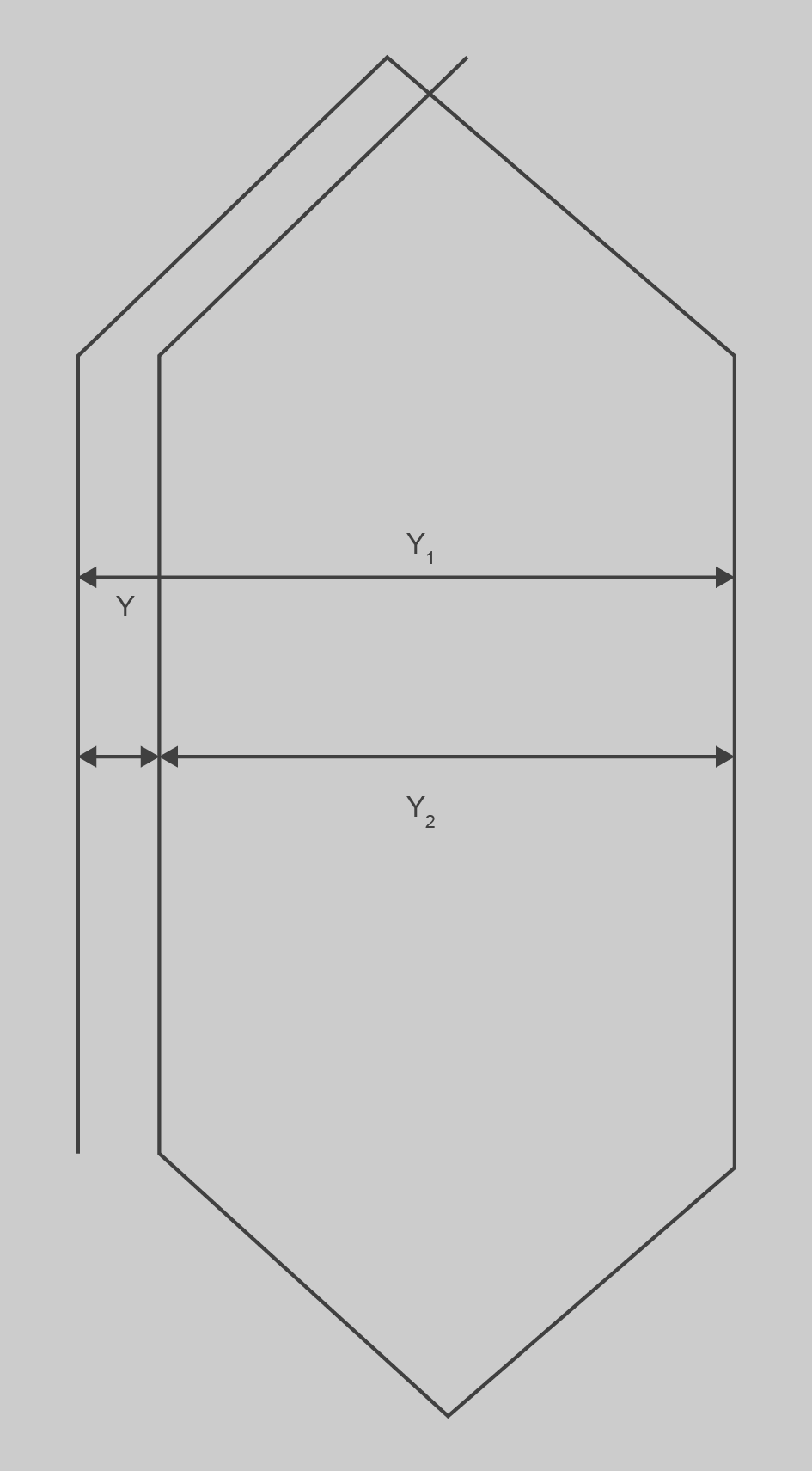
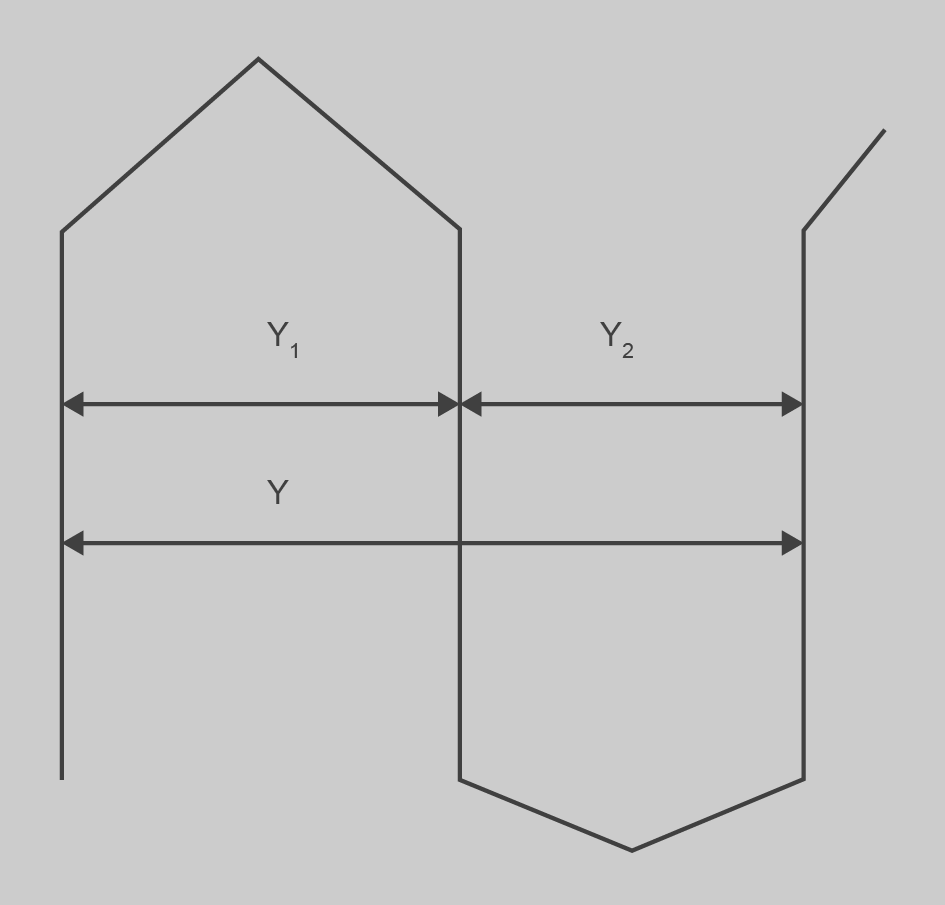
Pas de bobina Y1
Es coneix com a Y1 la distància entre els costats d’anada i tornada d’una mateixa bobina, o amplada de la bobina. Com l’amplada de la bobina ha de ser semblant a l’amplada polar, tenim:
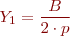
en què:
- p = parells de pols (o sigui, que 2·p = nombre total de pols principals)
Y1 es pot fer una mica més petit que l’amplada polar. En aquest cas es diu escurçat. Si es fa més gran que el pas polar es diu allargat.
Pas de connexió Y2
Y2 és la distància entre el costat de tornada d’una bobina i el d’anada de la següent connectada en sèrie.
Pas de bobinatge Y
Y és la distància entre els costats d’anada d’una bobina i el d’anada de la següent connectada en sèrie.
Bobinatges imbricats
Valor absolut
Quan posem un nombre o una variable entre barres verticals (com en |Y|) n’estem extraient el valor absolut, que és el valor numèric sense tenir en compte el signe.
En els bobinatges imbricats Y pot valer 1, 2, 3… Si |Y| > 1 tenim un bobinatge imbricat múltiple i si |Y| = 1 es tractarà d’un bobinatge imbricat simple. A més a més si Y és positiu, el bobinatge és no creuat, i si és negatiu, es tractarà d’un bobinatge creuat. En posar les escombretes al col·lector de delgues, quedaran a = (2·Y) circuits en paral·lel.
En un bobinatge imbricat (figura) es posen escombretes d’una amplada que curtcircuiti tantes delgues del col·lector com el valor de Y. La relació entre els passos de bobinatge és:

Bobinatges ondulats
En el cas dels bobinatges ondulats (figura) podem tenir bobinatges ondulats simples, si en fer la volta al rotor anem a parar al costat actiu següent o anterior al d’inici, o bobinatges ondulats múltiples, si anem a parar dos o més costats actius abans o després del d’inici.
La relació entre els passos de bobinatge és:

Cada cop que avancem una bobina o Y costats actius hem avançat un parell de pols, i per tant, en avançar tots els parells de pols que tingui la màquina hem d’anar a parar a Y + 1 si és creuat o a Y − 1 si és no creuat.

Per tant,
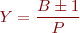
Perquè es pugui fer aquest bobinatge, Y ha de ser un nombre enter.
En els bobinatges ondulats simples només cal posar dues escombretes perquè només tindrem dues branques en paral·lel.
En un bobinatge múltiple, en lloc d’anar a parar al costat següent o anterior al d’inici, s’anirà a parar a m costats abans o després del d’inici, i per tant tenim que:

Per tant,

Càlcul de bobinatges de màquines de CC
Per calcular els passos d’un bobinatge partireu de les dades següents:
- K = nombre de ranures de la màquina
- u = nombre de costats actius per ranura i capa
- p = nombre de parells de pols de la màquina
- Tipus de bobinatge:
- Imbricat u ondulat
- Simple o múltiple (en el darrer cas, grau de multiplicitat)
- Creuat o no creuat
Amb aquestes dades ja es poden calcular els passos del bobinatge i dibuixar-ne l’esquema.
Exemple de càlcul de bobinatge imbricat simple
Calculeu el bobinatge d’una màquina de CC amb les característiques següents:
- Nombre de ranures k = 16
- Nombre de costats actius per ranura i capa u = 1
- Parells de pols p = 2
- Pas de bobinatge Y = 1
Solució
De les dades podem deduir:
- Nombre de bobines:

- Pas de bobina:
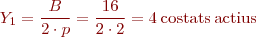
- Pas de connexió:

Amb aquestes dades podem dibuixar el bobinatge com es mostra a la figura.
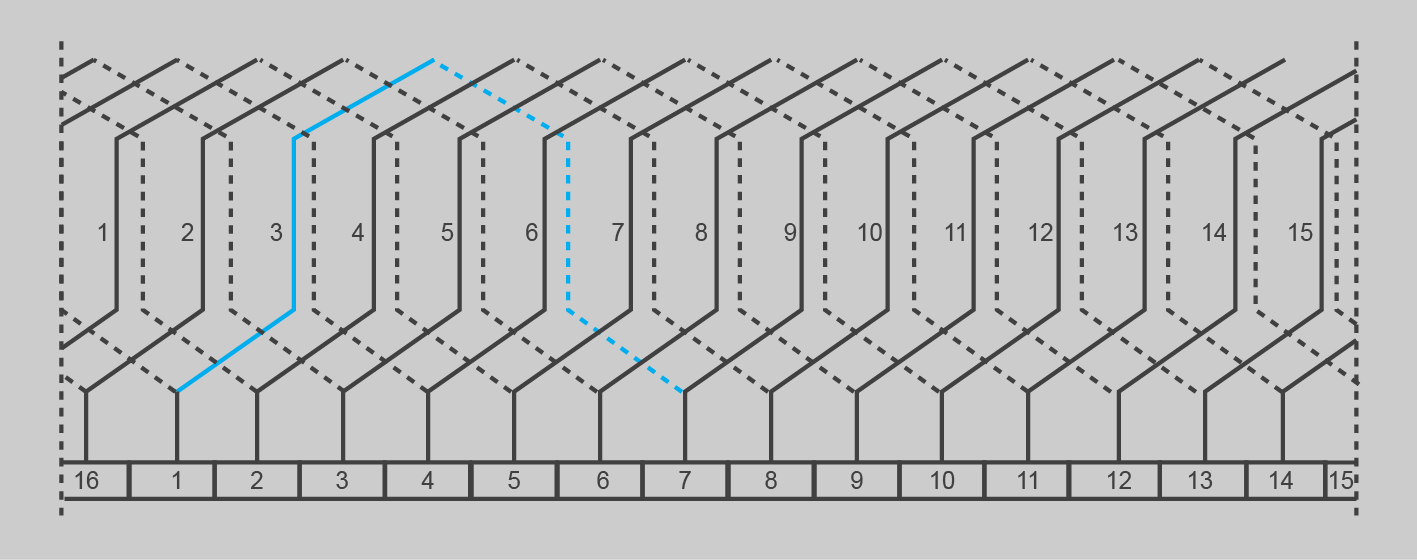
Exemple de càlcul de bobinatge ondulat simple
Calculeu el bobinatge d’una màquina de CC amb les característiques següents:
- Nombre de ranures k = 15
- Nombre de costats actius per ranura i capa u = 1
- Parells de pols p = 2
- Pas de bobinatge. Y = 1
Solució
De les dades podem deduir:
- Nombre de bobines:

- Pas de bobina:
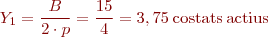
Agafarem Y1 = 4 costats actius
- Pas de bobinatge:
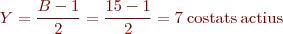
- Pas de connexió:

Amb aquests càlculs el dibuix del bobinatge queda de la manera que es mostra a la figura.
En el cas de bobinatges imbricats múltiples es dóna a Y un valor superior a 1. El grau de multiplicitat s’anomena m i pot tenir qualsevol valor entre 2 i 4, encara que normalment no passa de 2. Això vol dir que en retornar al mateix parell de pols per connectar bobines en sèrie no connectarem el que hi ha al costat del primer, sinó que en deixarem un de lliure abans d’arribar-hi (bobinatge no creuat) o el sobrepassarem (bobinatge creuat).
Si el nombre de bobines és múltiple de Y, es tancarà el bobinatge i n’haurem de fer un altre amb les bobines que han quedat sense connectar. En canvi, si B no és múltiple de Y, en fer la volta al rotor anirem a parar dos connectors abans o després d’on hem començat. En aquest cas seguirem tancant bobines fins que en fer la segona volta, quedi tancat del tot el bobinatge.
En el cas de bobinatges imbricats múltiples es posen escombretes d’un gruix tal que toquin simultàniament un nombre de delgues igual que l’ordre de multiplicitat m, i així quedaran 2·m circuits en paral·lel.
En un bobinatge imbricat múltiple denominarem:
- m = ordre de multiplicitat
- a = nombre de circuits en paral·lel
i així tindrem
- Y = m
- a = 2·m circuits en paral·lel
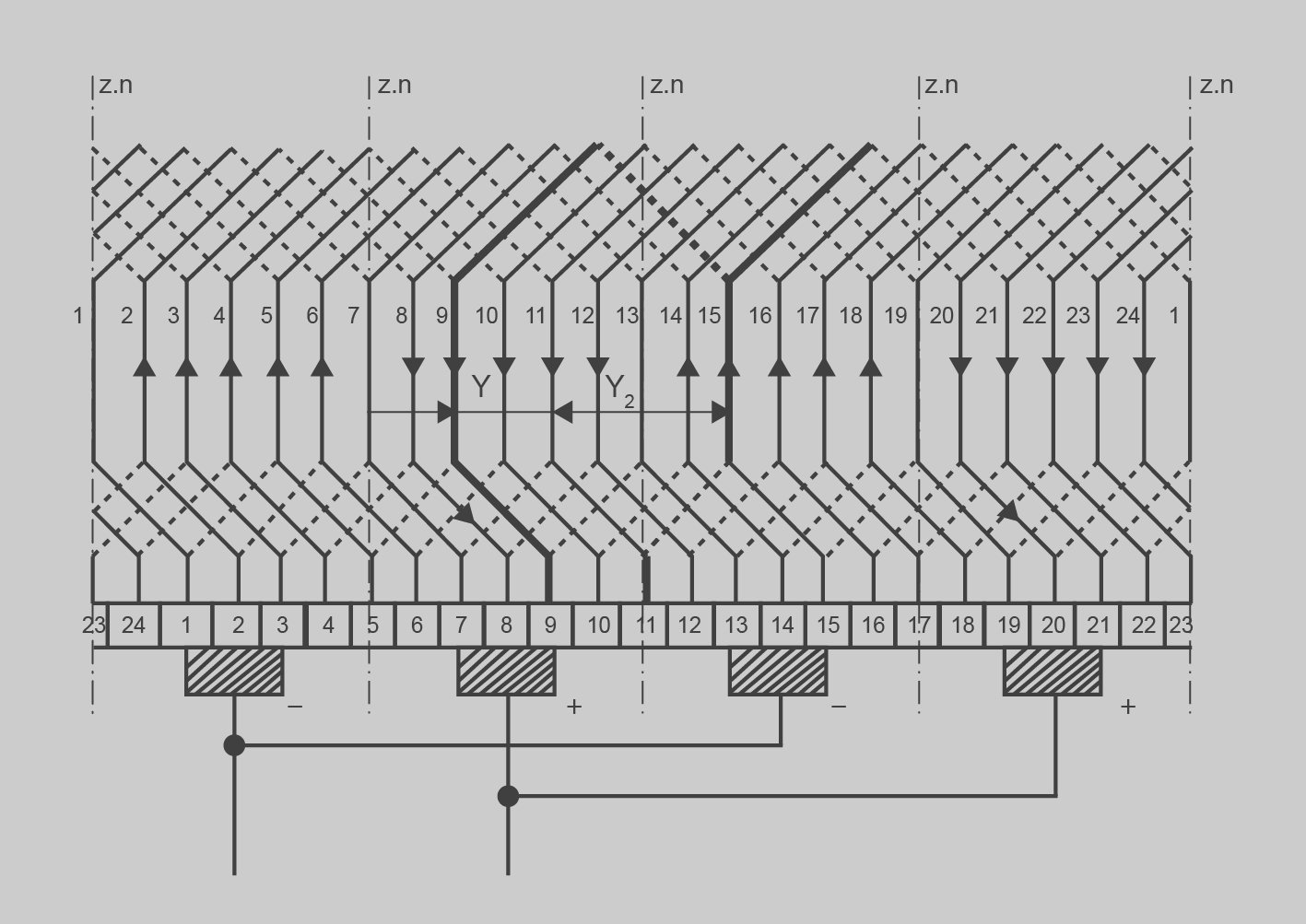
Exemple de càlcul de bobinatge imbricat múltiple
Calculeu un bobinatge imbricat doble per a un induït de:
- 2·p = 4
- k = 24
- u = 1
- No creuat
- m = 2
Solució
- Nombre de bobines:

- Delgues al col·lector:

- Pas de bobinatge:

- Pas de bobina:
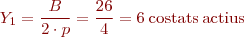
- Pas de connexió:

A la figura següent podem veure dibuixat aquest bobinatge:
Nombres primers entre ells
Es considera que dos nombres són primers entre ells si, tot i no ser nombres primers, no comparteixen cap divisor. És el cas, per exemple, del 33 i el 35, que no són primers (33 = 3·11 i 35 = 5·7) però que no tenen cap divisor comú.
Els bobinatges ondulats dobles poden ser simplement o doblement tancats. Si totes les bobines queden connectades en sèrie, és simplement tancat. Això es dóna si Y i B són primers entre ells.
En canvi, si Y i B tenen un divisor comú, tindrem un bobinatge de tancaments múltiples.
Les escombretes han d’ocupar tantes delgues com parells de branques hi hagi al circuit.
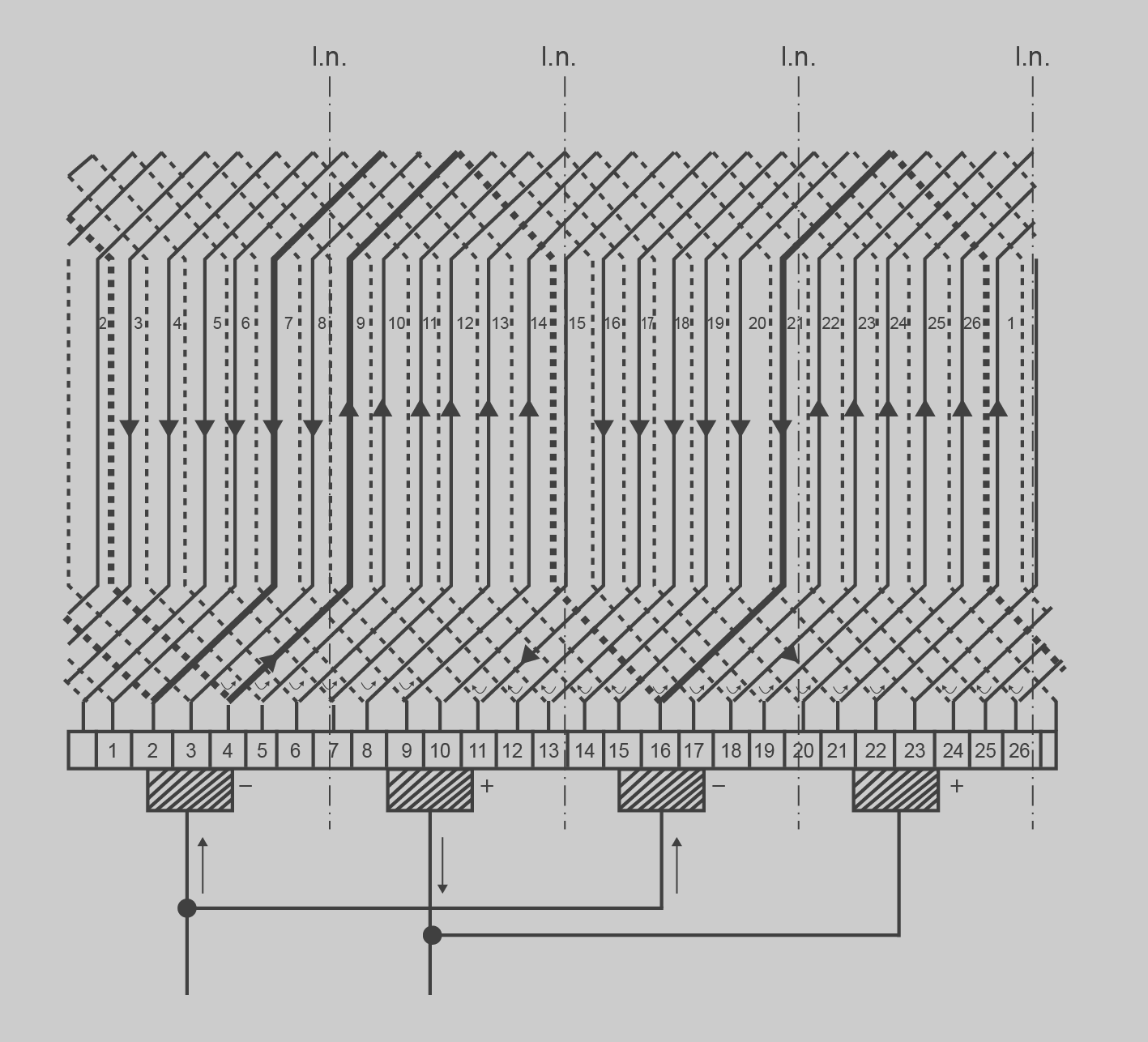
Exemple de càlcul de bobinatge ondulat doble
Calculeu un bobinatge ondulat doble per a un induït de:
- 2·p = 4 pols
- k = 26
- u = 1
- No creuat
- a = 2 (4 circuits derivats)
Solució
- Nombre de bobines:

- Delgues al col·lector:

- Pas de bobinatge:
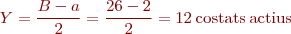
- Pas de bobina:
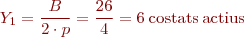
- Pas de connexió:

En la figura següent podem veure dibuixat aquest bobinatge:
Processos de muntatge i desmuntatge de màquines elèctriques de corrent continu
Tant en el procés de fabricació com en les diverses intervencions de manteniment cal muntar i desmuntar parts de les màquines elèctriques de corrent continu. En el cas de desmuntatge, cal tenir l’esquema d’especejament per poder tornar-lo a muntar o anotar on va cada peça que es treu i l’ordre d’extracció.
Per al desmuntatge d’una màquina de CC cal seguir les instruccions del fabricant.
Tot i que cada cas pot ser diferent, segons els complements i la complexitat de la màquina, en general es pot seguir un procediment com l’indicat tot seguit:
- Assegurar-se que tots els circuits elèctrics estan sense tensió.
- Desconnectar totes les connexions elèctriques i mecàniques de l’exterior i treure la màquina de la bancada.
- Desconnectar els connectors de l’interior de la caixa de connexions a l’estator si s’ha de retirar la caixa de connexions.
- Desconnectar els connectors de la corona portaescombretes a l’estator.
- Retirar les escombretes i embolicar el col·lector amb un aïllant.
- Extreure la coberta externa dels coixinets d’un extrem.
- Col·locar un material aïllant entre l’estator i el rotor.
- Retirar l’escut on és recolzat el rotor sencer d’una part.
- Fixar bé l’aïllant entre estator i rotor, i extreure l’escut que suporta el coixinet de l’altra part.
- Retirar el rotor si és necessari.
Un cop desmuntada la màquina es pot dur a terme la intervenció de manteniment adient. Els coixinets s’han de mantenir amb greix per protegir-los de la contaminació, i abans de muntar de nou el motor, eliminar el greix que sobra.
Per al muntatge de la màquina s’han de portar a terme les operacions contràries a les indicades, tenint en compte el parell d’estrenyiment recomanat pel fabricant per a cada peça que ho requereixi.
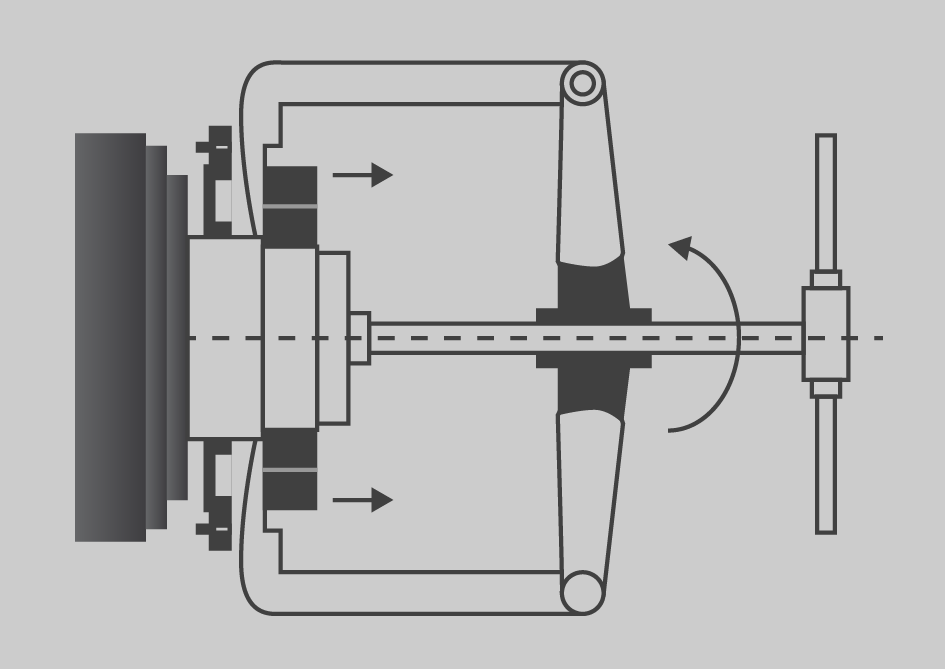
Per fer el manteniment calen les eines habituals i algunes d’especialitzades com l’extractor de rodaments, que podeu veure a la figura. Com els coixinets entren a pressió, cal una eina que permeti fer la força suficient per poder extraure’ls de la màquina.
Com es pot veure a la figura 24, l’extractor té una peça que enganxa els coixinets, va roscada sobre el cos de l’eina mateixa i es recolza en l’eix de la màquina. Girant la maneta es desplaça sobre el seu eix propi aplicant força entre l’eix de la màquina de CC i el coixinet, per extreure el coixinet del seu lloc.