Circuits combinacionals i seqüencials
Les portes lògiques donen solució a problemes que es plantegen en la vida quotidiana. Darrere de fets tan comuns com la utilització d’una calculadora, el control dels semàfors dels carrers, o fins i tot l’ús dels ordinadors trobem l’electrònica digital i les portes lògiques.
A mesura que els problemes són més complexos, també ho són els circuits per resoldre’ls. D’altra banda hi ha determinats processos que es donen de manera molt freqüent i que, per tant, es poden estandarditzar i tractar com un sol bloc.
Posem un exemple. Si una fàbrica ha de fer caragols d’unes determinades característiques, amb tota seguretat en comptes de fer-los un per un, de manera artesana, farà un motlle perquè surtin tots iguals.
Bé, doncs, en l’electrònica digital combinacional, i també en la seqüencial, el que es fa és desenvolupar blocs integrats que donen solucions a problemes concrets, sense haver de preocupar-nos de les portes que hi ha a dins i de com es troben interconnectades entre elles.
L’avenç progressiu de les tècniques d’integració ha permès la realització, en un circuit integrat, de sistemes combinacionals i seqüencials complexos formats per un gran nombre de portes lògiques. Aquesta integració redueix el nombre d’elements necessaris, ja que permet la combinació de diferents tipus de portes en un mateix bloc integrat, disminueix el temps de disseny i el nombre de connexions.
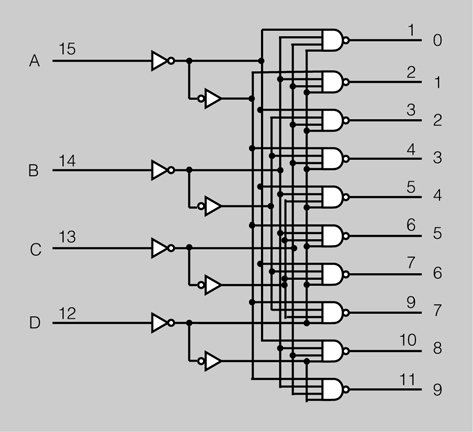
En la figura es mostra un exemple de circuit combinacional, amb quatre entrades i deu sortides.
Els circuits combinacionals són blocs formats per portes lògiques bàsiques (NOT, AND, OR, NAND, NOR, OR-exclusiva i NOR-exclusiva) que tenen diferents entrades i sortides, i en els quals els valors de la sortida o de les sortides dependran exclusivament del valor de les entrades en aquell instant.
Els blocs integrats combinacionals donen resposta a aplicacions de caire general, com ara codificadors, descodificadors, multiplexors, desmultiplexors, comparadors, etc.
Els circuits seqüencials són blocs formats per portes lògiques bàsiques que tenen diferents entrades i sortides, i en els quals els valors dels senyals de sortida no depenen solament dels valors dels senyals d’entrada, sinó també dels valors que les mateixes sortides tenien abans.
Els principals circuits seqüencials són els registres, els comptadors i els registres de desplaçament.
Multiplexors i desmultiplexors
L’enviament d’informació mitjançant senyals elèctrics d’un lloc a un altre es pot fer utilitzant una o diverses línies. Quan s’envia amb una sola línia estem parlant d’una transmissió en sèrie i quan es fa utilitzant diverses línies parlem d’una transmissió en paral·lel.
Si heu d’enviar una informació d’un byte i disposeu de vuit línies (cables de connexió) per a cada unitat de temps, podreu enviar un byte sencer. Si aquest mateix byte s’envia per una sola línia necessitareu 8 unitats de temps, ja que en aquest cas heu d’enviar un bit darrere l’altre, però necessitareu només un cable per connectar els dos llocs.
Per tant, el sistema que caldrà utilitzar dependrà d’aspectes econòmics, de la distància entre els llocs que volem comunicar i de la velocitat de transmissió de les dades. Aquesta necessitat de passar de diverses línies a una de sola (de paral·lel a sèrie) i a l’inrevés (de sèrie a paral·lel) porta a la multiplexació i a la desmultiplexació, respectivament.
Multiplexors
El multiplexor és un sistema digital que disposa de Nentrades d’informació i una única sortida. Mitjançant unes entrades de control, selecciona internament una de les entrades d’informació i la connecta a l’única sortida.
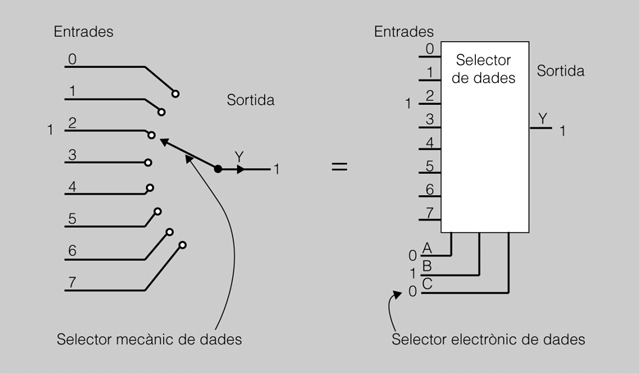
En la figura es pot veure com l’entrada de selecció és l’encarregada de connectar, en aquest cas, l’entrada corresponent al 2 amb la sortida Y. Gràficament es pot veure com l’entrada d’informació és en paral·lel i la sortida és en sèrie, només d’una línia.
Fixeu-vos com amb les entrades de control ABC (010 = 2) seleccionem l’entrada de dades 2, i com internament el que es fa és un pont entre aquesta entrada i la sortida (Y). Com que el nivell a l’entrada 2 és 1 (nivell alt), a la sortida trobem aquest nivell 1.
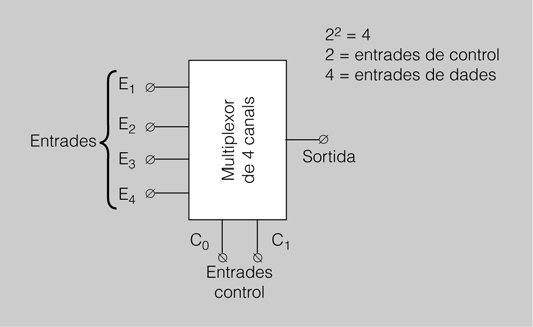
Als multiplexors s’ha de complir que les entrades d’informació N siguin igual a 2M, essent M el nombre d’entrades de control.
En la figura, podeu observar com les entrades per multiplexar poden ser com a màxim 4 si el nombre de línies de control és 2.
Circuit integrat 74151
El circuit integrat comercial 74151 és un petit xip de setze pius que implementa la funció de multiplexor de vuit línies.
En la taula es mostra com funciona el multiplexor de quatre línies: si les entrades de selecció prenen el valor 00, a la sortida apareix el senyal de l’entrada E1. Si les entrades de selecció prenen el valor 01, a la sortida apareix el senyal de l’entrada E2. Si les entrades de selecció prenen el valor 10, a la sortida apareix el senyal de l’entrada E3. I, finalment, si les entrades de selecció prenen el valor 11, a la sortida apareix el senyal de l’entrada E4.
| C1 | C0 | S |
|---|---|---|
| 0 | 0 | E1 |
| 0 | 1 | E2 |
| 1 | 0 | E3 |
| 1 | 1 | E4 |
Desmultiplexors
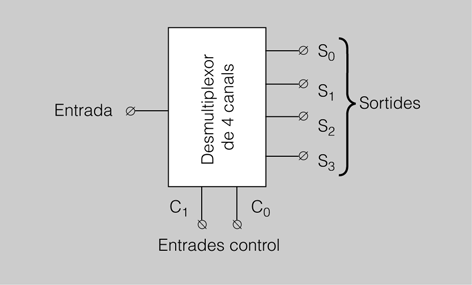
El desmultiplexor és un sistema digital que disposa d’una sola entrada d’informació i Nsortides. Mitjançant unes entrades de control, selecciona internament una de les sortides d’informació i la connecta a l’única entrada.
Com podeu comprovar, el seu funcionament és a l’inrevés que el multiplexor. Gràficament ho podeu acabar de veure a la figura i figura.
Circuit integrat 74155
El circuit integrat comercial 74155 és un petit xip de setze pius que implementa la funció de desmultiplexor d’una a vuit línies.
Als desmultiplexors s’ha de complir que les sortides d’informació N siguin igual a 2M, essent M el nombre d’entrades de control.
La taula és la taula de funcionament corresponent al desmultiplexor de quatre línies de la figura. Com podeu observar en la taula, la dada de l’entrada (1 o 0) apareixerà a la sortida seleccionada amb les línies de control C1 i C0.
| C1 | C0 | Entrada | S3 | S2 | S1 | S0 |
|---|---|---|---|---|---|---|
| 0 | 0 | E | 0 | 0 | 0 | E |
| 0 | 1 | E | 0 | 0 | E | 0 |
| 1 | 0 | E | 0 | E | 0 | 0 |
| 1 | 1 | E | E | 0 | 0 | 0 |
Connexió multiplexor-desmultiplexor
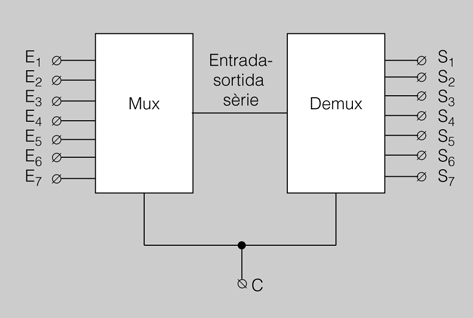
En la figura podeu veure l’aplicació del multiplexor (Mux) i desmultiplexor (Demux) per fer una transmissió de dades. El primer converteix la informació de paral·lel a sèrie; d’aquesta manera, la informació és enviada només amb una línia. La informació, quan arriba al desmultiplexor, es converteix de sèrie a paral·lel per tornar a tenir la informació original.
Fixeu-vos com tots dos elements estan connectats per un senyal de control. Aquest té la missió de sincronitzar els dos dispositius. Posarem un exemple. Quan el multiplexor està seleccionant l’entrada E2, el desmultiplexor ha d’estar seleccionant la sortida S2; quan el multiplexor selecciona l’entrada E3, el desmultiplexor ha de seleccionar la sortida S3, etc. És la manera perquè la informació a la sortida sigui la mateixa que a l’entrada.
Descodificadors i codificadors
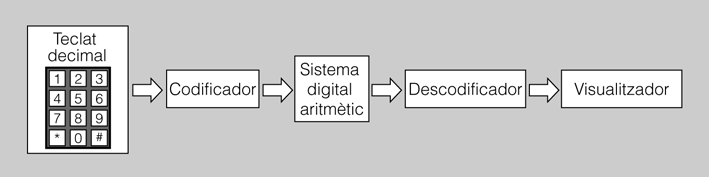
Per una banda, els sistemes digitals només treballen amb els bits 1 i 0 i, per l’altra, a les persones ens és difícil interpretar grans combinacions d’uns i zeros. Per donar resposta a aquesta situació, s’utilitzen els convertidors de codi, encarregats de traduir el nostre codi al llenguatge que entén el sistema digital. Si agafem com a exemple una calculadora, podem distingir tres grans blocs (figura):
- Un bloc codificador, on es produeix una codificació o conversió del codi decimal (teclat) a un codi binari (1 i 0).
- El sistema encarregat de fer les operacions que només interpreta bits 1 i 0.
- Un bloc descodificador que tradueix el resultat de l’operació, en binari, a un llenguatge que podem interpretar, en decimal.
Traducció
Els codificadors tradueixen el llenguatge que nosaltres utilitzem al codi que entén el sistema digital. Els descodificadors tradueixen el llenguatge que utilitza el sistema digital a un llenguatge que nosaltres entenem.
Els codificadors són sistemes combinacionals que s’encarreguen de transformar una sèrie de senyals sense codificar en un conjunt de senyals codificats.
Els descodificadors són circuits integrats digitals que fan la conversió d’un codi binari, normalment el BCD, en una forma sense codificar.
Descodificadors
Els descodificadors tradueixen el llenguatge que utilitza el sistema digital a un llenguatge que nosaltres puguem entendre.
Els descodificadors són circuits combinacionals que si tenen n nombre d’entrades poden presentar fins a 2n nombre de sortides.
| Entrades | Sortides | ||||
|---|---|---|---|---|---|
| A | B | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Descodificador de dues entrades
Un descodificador de dues entrades té les següents característiques:
- Nombre d’entrades: n = 2
- Nombre de sortides: N = 2n = 4
En la taula es mostra la taula de veritat d’aquest circuit. El seu funcionament és molt senzill: per a cada combinació binària de les entrades, es posa a 1 la sortida corresponent.
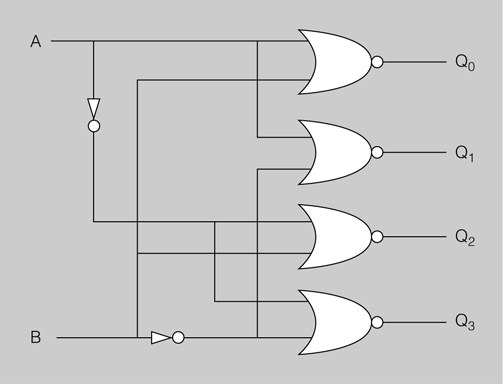
En la figura es mostra el circuit amb portes lògiques que implementa la funció de descodificador de dues entrades.
Descodificadors BCD/decimal
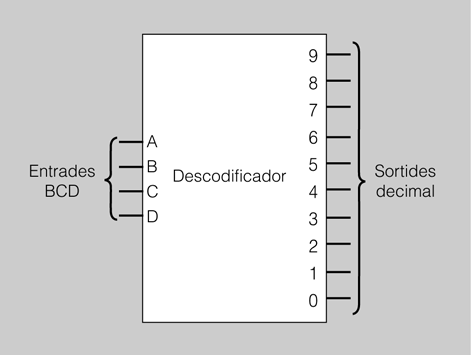
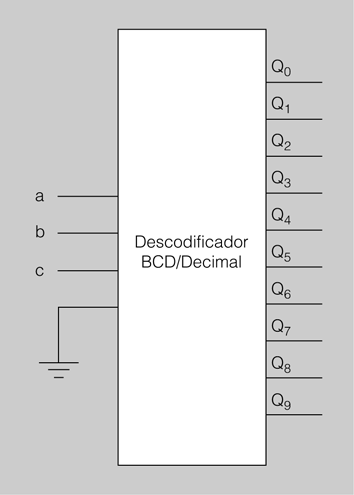
Els descodificadors que més s’utilitzen són els descodificadors BCD/decimal. En la figura es mostra un diagrama d’aquests circuits.
Circuit integrat 7442
El circuit integrat comercial 7442 és un petit xip de catorze pius que implementa la funció de descodificador BCD/decimal.
Els descodificadors tenen quatre línies d’entrada que formen un codi BCD. A la sortida tenen deu línies, de manera que es posa a 1 la sortida que correspon al nombre decimal representat a l’entrada, mentre que les altres sortides es mantenen a 0.
En la taula es mostra la taula de veritat del descodificador BCD/decimal.
| Entrades | Sortides | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | Q9 | Q8 | Q7 | Q6 | Q5 | Q4 | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Descodificadors BCD/set segments
Per veure el funcionament d’aquest tipus de circuit, abans cal fer esment dels dispositius visualitzadors de set segments.
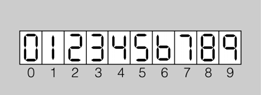
Els visualitzadors de set segments, que podeu veure en la figura, s’utilitzen per visualitzar nombres decimals. Els set segments s’identifiquen amb les lletres a, b, c, d, e, fig.
En la figura podeu observar com s’aconsegueix la visualització dels deu dígits decimals (del 0 al 9). Per exemple, si s’activen tots menys el segment g es visualitza el zero. En canvi, si s’activen el segment a, b ic, es visualitza el 7, i si s’activen tots els segments, el 8.
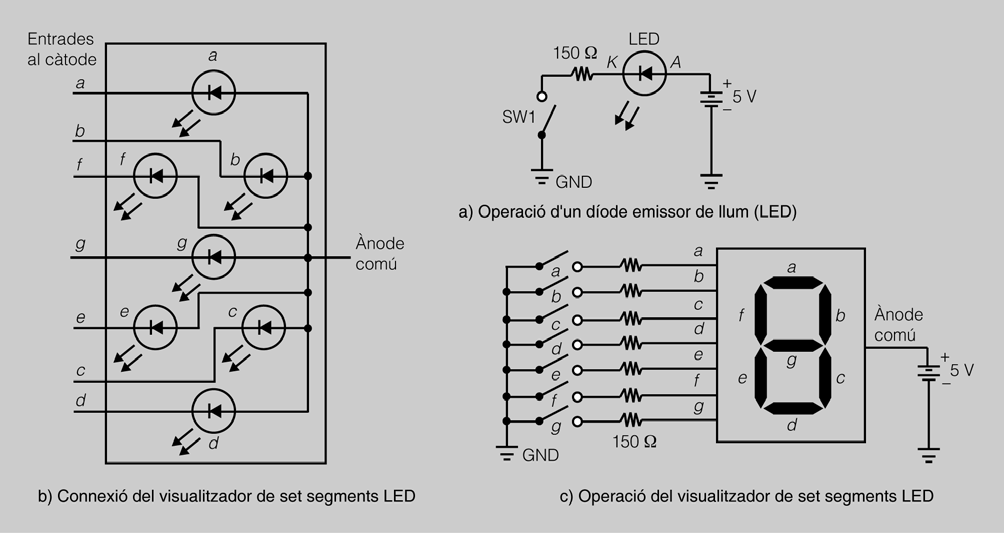
En la figura podeu veure la composició interna d’un visualitzador de set segments, el seu funcionament elèctric i la connexió.
Cada segment està fet a partir d’un díode LED. Quan aquest díode LED és travessat pel corrent elèctric, emet radiacions lluminoses.
Els elements del visualitzador sempre han de portar una resistència limitadora. El valor d’aquesta resistència es calcula mitjançant la següent equació:

Pel que fa al càlcul, es considera el voltatge LED aproximadament de 2 V i el corrent LED necessari al voltant dels 20 mA, per a LEDs estàndard.
Tal com s’aprecia en la figura, per a una alimentació VCC de 5 V la resistència limitadora hauria de ser d’uns 150 Ω. Col·locant una resistència limitadora de 500 Ω, podríeu connectar el mateix visualitzador a un voltatge d’alimentació de 12 V. Podeu comprobar que en la connexió del visualitzador de set segments, cada segment conté un LED. Tots els ànodes estan connectats entre si (connexió ànode comú) i a positiu. Per tant, quan en el càtode d’un determinat díode apareix un nivell baix, o 0 lògic, el díode emetrà llum.
També podeu trobar visualitzadors amb la connexió de càtode comú. En aquest cas, el segment s’encendrà quan hi apliqueu un nivell alt (1 lògic).
En la figura es representa el diagrama en bloc d’un descodificador BCD/ set segments. Com podeu apreciar, hi ha les quatre entrades corresponents al codi BCD i set sortides, una per a cada segment del visualitzador.
Circuit integrat 7447
El circuit integrat comercial 7447 és un petit xip de setze pius que implementa la funció de descodificador BCD/set segments.
En la taula es mostra el funcionament del descodificador BCD/set segments.
| Entrades | Sortides | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | a | b | c | d | e | f | g |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Implementació de funcions lògiques amb descodificadors
Una de les aplicacions dels descodificadors és la d’implementar funcions lògiques.

| c | b | a | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Per exemple, si volem implementar amb un descodificador la funció lògica  , els passos que haurem de seguir seran els següents:
, els passos que haurem de seguir seran els següents:
- Escrivim la taula de veritat de la funció, com es mostra en la taula.
- Utilitzem un descodificador amb un nombre d’entrades igual o més gran que el nombre de variables de la funció. Com que, en aquest cas, tenim tres variables (a, b, c) utilitzarem un descodificador BCD/decimal.
- Com es mostra en la figura, connectem les variables de la funció a les entrades del descodificador BCD/decimal. L’entrada de més pes del descodificador la connectem a massa, ja que no la utilitzem.
- Mirem les combinacions de les variables que donen 1:
- Q1 = 001
- Q3 = 011
- Q4 = 100
- Q7 = 111
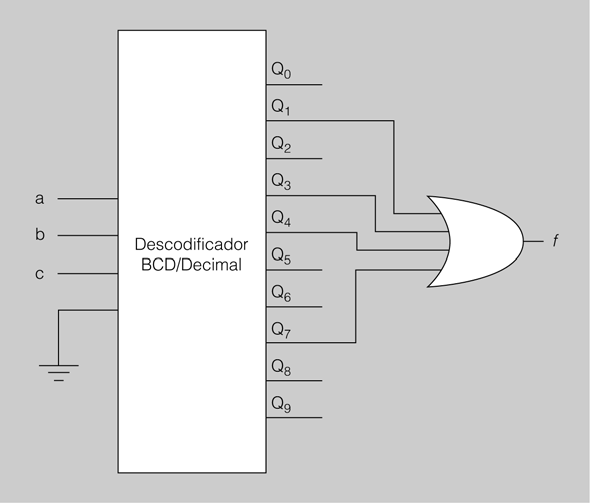
- Finalment, connectem a una porta OR les sortides del descodificador que es posen a 1. En la figura es mostra el circuit final.
D’aquesta manera, a la sortida de la porta OR obtindrem la funció f.
Codificadors
Els codificadors tradueixen el llenguatge que utilitzem (normalment, codi decimal) al codi que entén el sistema digital (normalment, codi binari).
Els codificadors són circuits combinacionals que si tenen 2n nombre d’entrades presenten n nombre de sortides.
Codificador decimal/BCD
Un dels tipus de codificador més utilitzat és el codificador decimal/BCD. En aquest circuit, quan s’activa una de les entrades decimals, les sortides agafen l’estat corresponent al seu codi BCD. En la taula es mostra la seva taula de veritat.
Els codificadors decimal/BCD són prioritaris, això vol dir que si hi ha més d’una entrada activada, la sortida que s’activarà correspondrà a l’entrada de major pes o de menor pes, segons la seva estructura interna.
Aquests codificadors tenen la sortida Y0 que s’activa en el cas que totes les entrades estiguin a zero. D’aquesta manera es distingeix entre dos casos:
- Quan s’activa l’entrada E0, les sortides Q3, Q2, Q1 i Q0 estan a zero i la sortida Y0, també.
- Quan no hi ha cap entrada activada, les sortides Q3, Q2, Q1 i Q0 estan a zero i la sortida Y0 es posa a 1.
Circuit integrat 74147
El circuit integrat comercial 74147 és un petit xip de setze pius que implementa la funció de codificador decimal/BCD.
| Entrades | Sortides | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E9 | E8 | E7 | E6 | E5 | E4 | E3 | E2 | E1 | E0 | Y0 | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | X | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | X | X | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | X | X | X | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | X | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | X | X | X | X | X | X | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | X | X | X | X | X | X | X | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | X | X | X | X | X | X | X | X | 0 | 1 | 0 | 0 | 0 |
| 1 | X | X | X | X | X | X | X | X | X | 0 | 1 | 0 | 0 | 1 |
Circuits comparadors
Les aplicacions de lògica digital combinacional requereixen moltes vegades realitzar la comparació entre dades binàries procedents de diferents fonts.
Un circuit comparador és aquell que pot comparar dos nombres binaris (A i B) de n bits cadascun i determinar si són iguals (A = B), o si no ho són, quin és més gran (A > B) o més petit que l’altre (A < B).
Els comparadors són circuits combinacionals que indiquen, a la seva sortida, la relació d’igualtat o desigualtat entre dos nombres (A i B) de n bits cadascun.
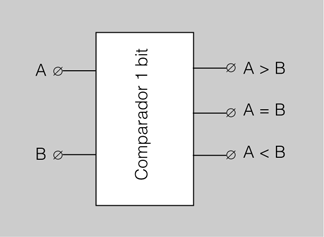
El circuit comparador més senzill és aquell que permet fer la comparació entre dos nombres d’un bit. En la figura podeu veure la seva representació.
Com podem observar, hi ha, com a entrades, els dos nombres per comparar A i B i les tres sortides possibles A > B, A = B i A < B.
La taula de veritat d’aquest circuit comparador d’un bit es mostra a la taula.
Circuit integrat 7485
El circuit integrat comercial 7485 és un petit xip de setze pius que permet comparar dos nombres binaris de 4 bits.
| Entrades | Sortides | |||
|---|---|---|---|---|
| A | B | A > B | A = B | A < B |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
Circuits seqüencials
-

- Un semàfor és un exemple típic de sistema seqüencial.
Fixem-nos en el funcionament d’un semàfor qualsevol del nostre municipi. Un semàfor és un sistema digital típic i les seves sortides són les següents:
- llum vermell per a vehicles
- llum taronja per a vehicles
- llum verd per a vehicles
- llum vermell per a vianants
- llum verd per a vianants
Aquestes cinc sortides només poden prendre dos valors diferents: llum encès o llum apagat. Com a única entrada possible, un semàfor pot presentar el polsador perquè els vianants puguin dir al semàfor que volen creuar el carrer.
Imaginem-nos que arribem a un semàfor passejant. Volem creuar el carrer però el llum dels vianants està en vermell i els vehicles circulen perquè tenen el llum verd encès. Com que tenim pressa, premem el polsador del semàfor i, després de pocs segons, el semàfor dels vehicles es posa en vermell (passant primer pel taronja) i el semàfor dels vianants es posa en verd. Fins aquí tot molt bé: quin semàfor més amable! Ens ha obeït de seguida.
Però què passarà si ara, amb el llum verd per als vianants encès, tornem a prémer el polsador? Doncs que el semàfor no ens farà ni cas i, transcorreguts uns quants segons, continuarà amb la seva seqüència de funcionament normal, deixant passar els vehicles i encenent el llum vermell per als vianants. Si pogués parlar, el semàfor ens diria alguna cosa semblant a: “No cal que tornis a prémer el polsador que ja t’he entès a la primera! Això sí: espavila’t perquè en pocs segons jo continuaré fent la meva feina i no et deixaré passar!”.
Això significa que el semàfor no sempre dóna les mateixes sortides per a una mateixa combinació de les entrades. Aquest semàfor és un exemple típic de sistema digital seqüencial.
Cronòmetre
Penseu en un cronòmetre digital amb un polsador d’inici/aturada i un polsador de reinicialització o RESET per tornar a zero. És un sistema digital seqüencial? Per què?
En un sistema digital seqüencial, els valors dels senyals de sortida no depenen solament dels valors dels senyals d’entrada, sinó també dels valors que les mateixes sortides tenien abans.
Us podeu trobar amb llibres tècnics que anomenen al nivell alt i al nivell baix estat de SET i estat de RESET, respectivament.
Els circuits seqüencials elementals són els biestables. A partir de biestables es poden construir circuits seqüencials més complexos com, per exemple, els comptadorsi els registres de desplaçament.
Biestables: latches i flip-flops
Un biestable és un circuit digital seqüencial que pot tenir dos estats estables a la sortida denominats nivell alti nivell baix, en els quals es pot mantenir indefinidament.
Un biestable canvia l’estat de la seva sortida segons les seves entrades i l’estat previ de la sortida.
Un flanc...
… és una transició d’un senyal digital de 0 a 1 o d’1 a 0. Si la transició és de 0 a 1 s’anomena flanc positiu o flanc de pujada. Si la transició és d’1 a 0 s’anomena flanc negatiu o flanc de baixada.
Els dispositius biestables es divideixen en dues categories:
- Latches: són biestables asíncrons. Això vol dir que no utilitzen cap senyal de sincronització o rellotge.
- Flip-flops: són biestables síncrons. Això vol dir que la seva sortida canvia d’estat únicament en un instant específic d’una entrada de sincronització denominada rellotge (habitualment, en un instant concret anomenat flanc).
-
- Flanc positiu
-
- Flanc negatiu
Els flip-flops es poden classificar segon el tipus de senyal de rellotge que utilitzen:
- Flip-flop disparat per flanc positiu: la sortida del flip-flop canvia quan el senyal de rellotge fa una transició de 0 a 1.
- Flip-flop disparat per flanc negatiu: la sortida del flip-flop canvia quan el senyal de rellotge fa una transició d’1 a 0.
Latch S-R (SET-RESET)
El funcionament del latch S-R és el següent:
- Si posem l’entrada S (SET) a 1 i deixem l’entrada R (RESET) a 0, la sortida
 del latch S-R es posa a 1: és el que s’anomena estat de SET.
del latch S-R es posa a 1: és el que s’anomena estat de SET. - Si posem l’entrada R (RESET) a 1 i deixem l’entrada S (SET) a 0, la sortida
 del latch S-R es posa a 0: és el que s’anomena estat de RESET.
del latch S-R es posa a 0: és el que s’anomena estat de RESET. - Si posem les dues entrades S i R a 0, les sortides no canvien: conserven l’estat. Això vol dir posar el mateix valor que tenien abans de canviar l’estat de les entrades. Aquesta característica és molt important, perquè el latch “memoritza” el seu estat anterior.
- La sortida
 sempre té el valor contrari a la sortida
sempre té el valor contrari a la sortida  (d’això se’n diu que les dues sortides són complementàries).
(d’això se’n diu que les dues sortides són complementàries).
La taula de veritat del latch S-R es mostra en la taula.
-
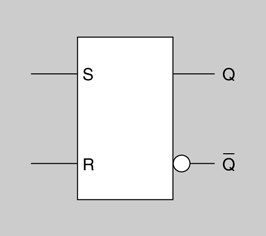
- Símbol lògic del latch S-R
| Entrades | Sortides | |||
|---|---|---|---|---|
| S | R |  |  | Comentaris |
| 0 | 0 |  |  | Les sortides no canvien. Es queden en l’estat anterior |
| 1 | 0 | 1 | 0 | Estat de SET |
| 0 | 1 | 0 | 1 | Estat de RESET |
| 1 | 1 | ? | ? | Condició no vàlida |
I què passa quan posem les dues entrades del latch S-R a 1? Doncs que, a causa del funcionament intern del latch S-R, no podem predir quines sortides obtindrem.
No hem de posar mai les dues entrades del latch S-R a 1 simultàniament perquè no podem predir quin valor tindran les seves sortides. Aquesta imprecisió del valor de les sortides podria provocar problemes greus al circuit on estigués connectat el latch S-R.
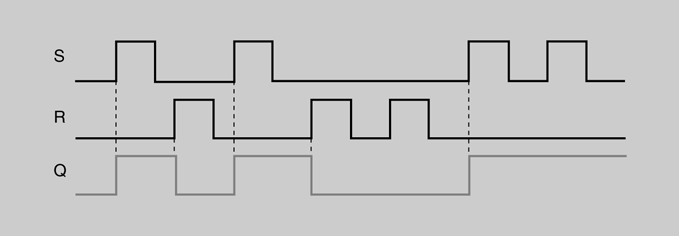
En la figura podem veure l’evolució amb el temps de les les formes d’ona de les entrades i la sortida d’unlatch S-R. Se suposa que Q es troba inicialment a nivell baix. Observeu que en cap moment les dues entrades es troben a nivell alt simultàniament.
Latch S-R amb entrada d'habilitació
El nom EN d’una entrada d’habilitació ve de la paraula anglesa enable, que vol dir habilitació.
A un latch S-R se li pot afegir una nova entrada: l’entrada d’habilitació EN.
-
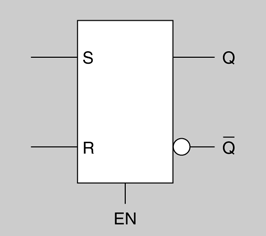
- Símbol lògic del latch S-R amb entrada d'habilitació
La funció d’aquesta entrada EN és molt senzilla:
- Quan l’entrada EN està a nivell alt, el latch està habilitat i funciona com un latch S-R normal.
- Quan l’entrada EN està a nivell baix, simplement el latch S-R no fa res: per molt que canviem el valor de les entrades S i R, les sortides conserven l’estat anterior.
La taula de veritat d’aquest latchS-R amb entrada d’habilitació es mostra en la taula.
| Entrades | Sortides | ||||
|---|---|---|---|---|---|
| EN | S | R |  |  | Comentaris |
| 1 | 0 | 0 |  |  | Les sortides no canvien. Es queden en l’estat anterior |
| 1 | 1 | 0 | 1 | 0 | Estat de SET |
| 1 | 0 | 1 | 0 | 1 | Estat de RESET |
| 1 | 1 | 1 | ? | ? | Condició no vàlida |
| 0 | X | X |  |  | Latch no habilitat. Les sortides no canvien |
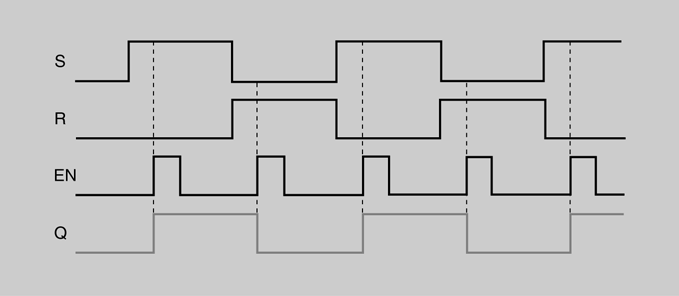
En la figura podem veure les formes d’ona de les entrades i la sortida d’un latch S-R amb habilitació. Se suposa que Q es troba inicialment a nivell baix.
Flip-flop S-R
En la taula es mostra la taula de veritat d’un flip-flop S-R disparat per flanc positiu. Com es pot veure, el seu funcionament és similar al del latch S-R. L’única diferència és que les sortides només canvien en l’instant en què el senyal CLK passa de nivell baix a nivell alt.
| Entrades | Sortides | ||||
|---|---|---|---|---|---|
| CLK | S | R |  |  | Comentaris |
| X | X | X |  |  | No hi ha flanc de CLK: les sortides no canvien |
 | 0 | 0 |  |  | Les sortides no canvien |
 | 1 | 0 | 1 | 0 | Estat de SET |
 | 0 | 1 | 0 | 1 | Estat de RESET |
 | 1 | 1 | ? | ? | Condició no vàlida |
-
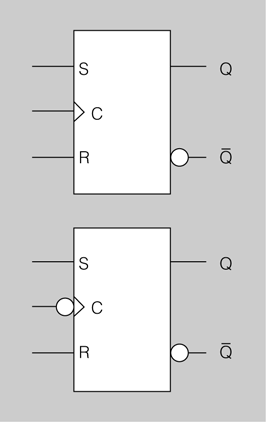
- Flip-flops S-R disparats per flanc positiu (superior) i per flanc negatiu (inferior)
Com en el cas del latch S-R, mai no hem de posar les entrades S i R del flip-flop S-R simultàniament a nivell alt, perquè no podem predir quin valor tindran les seves sortides. Aquesta imprecisió del valor de les sortides podria provocar problemes greus al circuit on estigués connectat el flip-flop S-R.
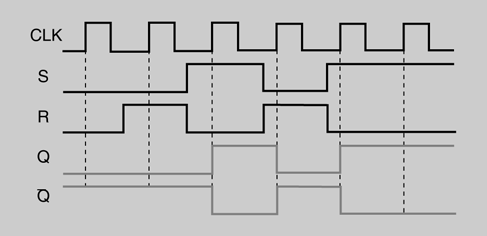
En la figura podem veure les formes d’ona de les entrades i la sortida d’un flip-flop S-R disparat per flanc positiu. Se suposa que Q es troba inicialment a nivell baix.
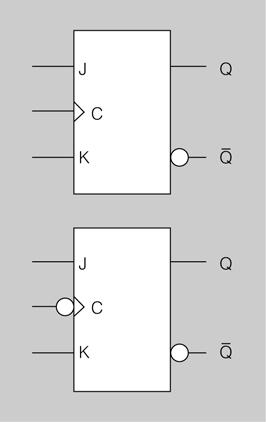
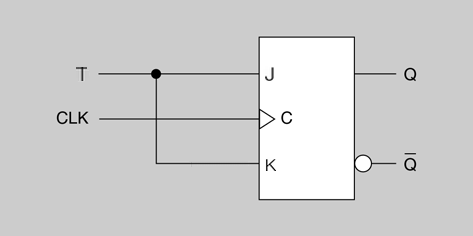
Flip-flop J-K
Les denominacions J i K...
… per a les entrades del flip-flop J-K no tenen cap significat conegut, excepte el fet que són dues lletres consecutives de l’alfabet.
El flip-flop J-K és un dels tipus de flip-flop més utilitzats.
El funcionament del flip-flop J-K és idèntic al del flip-flop S-R en els estats d’operació SET, RESET i no-canvi. La diferència resideix en el fet que el flip-flop J-K no té condicions no vàlides com passa amb el flip-flop S-R (ara sí hi pot haver dos uns a les entrades).
| Entrades | Sortides | ||||
|---|---|---|---|---|---|
| CLK | J | K |  |  | Comentaris |
| X | X | X |  |  | No hi ha flanc de CLK: les sortides no canvien |
 | 0 | 0 |  |  | Les sortides no canvien. |
 | 1 | 0 | 1 | 0 | Estat de SET |
 | 0 | 1 | 0 | 1 | Estat de RESET |
 | 1 | 1 |  |  | Basculació: la sortida canvia al seu estat oposat |
Com podem observar en la taula de veritat del flip-flop J-K (taula), ara ja no hi ha combinacions no vàlides de les entrades, com passava al flip-flop S-R. Quan les dues entrades J i K es posen a nivell alt, la sortida canvia al seu estat oposat. És a dir, ens podem trobar amb dues d’aquestes situacions:
- Si la sortida estava a nivell alt abans del flanc de rellotge, passarà a nivell baix.
- Si la sortida estava a nivell baix abans del flanc de rellotge, passarà a nivell alt.
Circuit integrat 74HC112
El circuit integrat comercial 74HC112 és un petit xip de setze pius que conté dos flip-flops J-K disparats per flanc descendent.
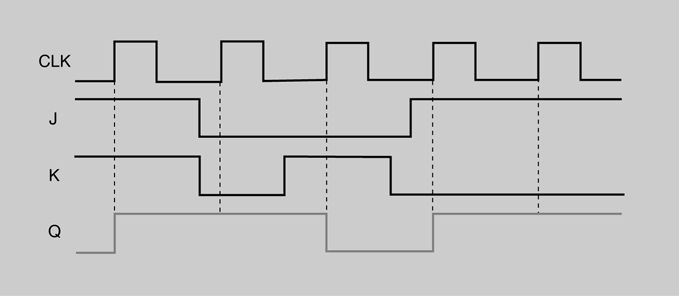
En la figura podem veure les formes d’ona de les entrades i la sortida d’un flip-flop J-K disparat per flanc positiu. Se suposa que Q es troba inicialment a nivell baix.
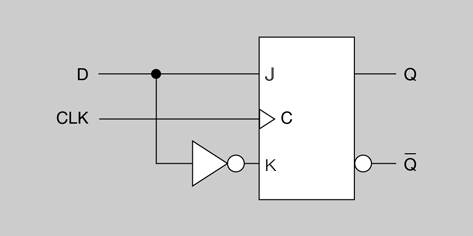
Flip-flops D i T
El flip-flop D està construït a partir d’un flip-flop J-K al qual s’han unit les seves entrades J i K mitjançant un inversor, tal com es mostra en la figura. La taula de veritat d’aquest flip-flop D és molt senzilla (taula).
-
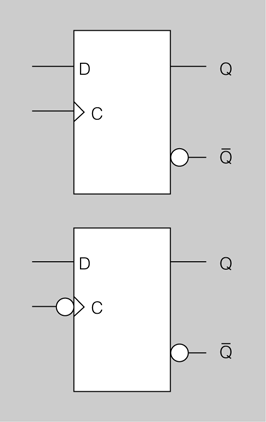
- Flip-flop D disparat per flanc positiu (superior) i per flanc negatiu (inferior)
| Entrades | Sortides | |||
|---|---|---|---|---|
| D | CLK |  |  | Comentaris |
| 0 |  | 0 | 1 | Estat de RESET |
| 1 |  | 1 | 0 | Estat de SET |
Flanc positiu o flanc negatiu?
Quan un flip-flop es dispara per flanc negatiu se simbolitza amb un petit cercle a l’entrada del rellotge. Si el flip-flop es dispara per flanc positiu el petit cercle no apareix en el seu símbol.
Com veiem en la taula, la sortida Q conserva el valor que té l’entrada D just en l’instant en el qual es produeix la transició positiva del rellotge. Aquesta propietat fa que el flip-flop D s’utilitzi molt com a element de memòria.
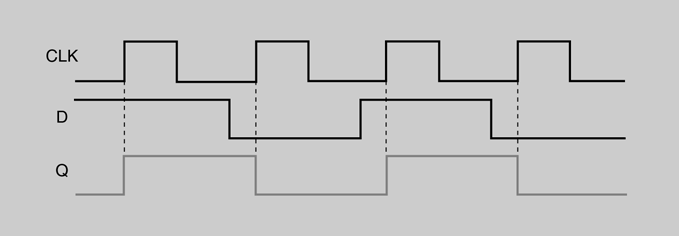
En la figura podem veure les formes d’ona de les entrades i la sortida d’un flip-flop D disparat per flanc positiu. Se suposa que Q es troba inicialment a nivell baix.
-
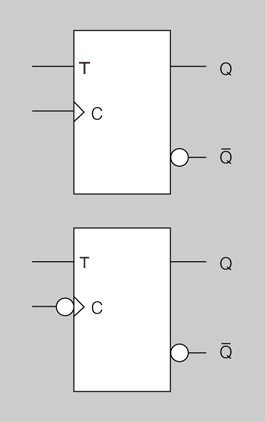
- Flip-flop T disparat per flanc positiu (superior) i per flanc negatiu (inferior)
El flip-flop T està construït a partir d’un flip-flop J-K al qual s’han unit les seves entrades J i K directament, tal com es mostra en la figura. La taula de veritat d’aquest flip-flop T és molt senzilla (taula).
| Entrades | Sortides | |||
|---|---|---|---|---|
| T | CLK |  |  | Comentaris |
| 0 |  |  |  | No hi ha canvi d’estat |
| 1 |  |  |  | Canvi d’estat forçat |
Com veiem en la taula, la sortida Q canvia el valor que tenia si hi ha un 1 a l’entrada T just en l’instant en el qual es produeix la transició positiva del rellotge. Aquesta propietat fa que el flip-flop T s’utilitzi molt com a element comptador o com a complement d el rellotge.
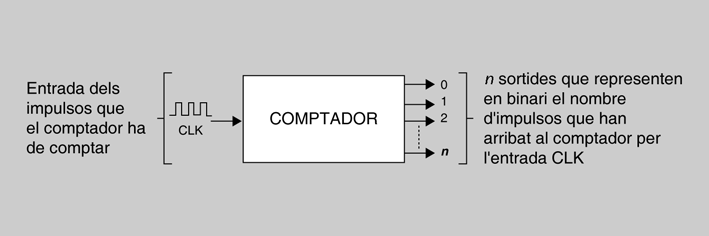
Comptadors
Un comptador (figura) és un circuit format per flip-flops T, que té una entrada d’impulsos (anomenada entrada de rellotge o CLK) i un nombre de sortides n que representen en codi binari, en cada moment, el nombre d’impulsos que li arriben a l’entrada de rellotge.
-

- Un cronòmetre és un exemple molt clar de comptador digital
La importància dels comptadors dins del món dels sistemes digitals és molt gran. Només cal pensar en el gran nombre d’aplicacions que poden tenir: detecció del nombre de vehicles que entren en un pàrking, recompte de les peces elaborades en una fàbrica, realització de funcions de cronometratge, etc.
Els comptadors digitals tenen les característiques següents:
- Mòdul: és el nombre de combinacions diferents que té un comptador a la seva sortida. Per exemple, si un comptador té 4 bits de sortida i compta des de 0000 fins a 1111, es diu que és de mòdul 16 o, de forma abreujada, és diu que és MOD16.
- Compte ascendent o descendent: gairebé tots els comptadors digitals tenen un bit d’entrada per seleccionar si el compte es fa de manera ascendent o descendent.
- Operació asíncrona o síncrona: als comptadors asíncrons, els flip-flops no comparteixen el mateix senyal de rellotge. Als comptadors síncrons, tots els seus flip-flops comparteixen el mateix senyal de rellotge. Els més utilitzats són els comptadors síncrons.
- Entrada d’esborrat: molts comptadors disposen d’un bit d’entrada que, quan es posa a zero, fa que totes les sortides es posin a nivell baix (RESET).
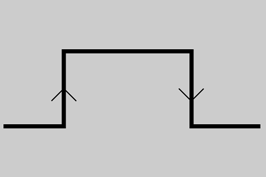
- Entrada amb flanc ascendent o descendent: els comptadors amb flanc ascendent canvien la seva sortida quan en el senyal de rellotge hi ha una transició de baix a alt. Els comptadors amb flanc descendent canvien la seva sortida quan en el senyal de rellotge hi ha una transició d’alt a baix. En la figura es mostra un pols de rellotge amb els seus flancs ascendent i descendent.
Els comptadors més utilitzats són els de quatre bits de sortida
Els comptadors de quatre bits de sortida poden ser:
- De mòdul 16 (MOD16): compten des de 0000b fins a 1111b (és a dir, de 0 a 15 en decimal, o de 0 a F en hexadecimal).
- De mòdul 10 (MOD10): compten des de 0000b fins a 1001b (és a dir, de 0 a 9 en decimal). Quan les sortides d’aquests comptadors estan a 1001b i hi ha un nou pols de rellotge a l’entrada, les sortides tornen a 0000b.
Els comptadors dels PLC
La majoria de comptadors que porten incorporats els autòmats programables compten fins a valors superiors a 30.000 impulsos.
Per comptar nombres més grans de 16 s’utilitzen diversos comptadors de quatre bits connectats entre ells.
Comptador binari síncron de quatre bits 74163
-
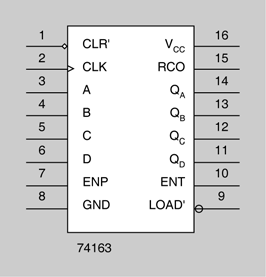
- 74163: comptador binari síncron de 4 bits
El xip 74163 és un exemple de circuit integrat comptador binari de quatre bits.
La utilitat de cada piu d’aquest circuit comptador es descriu a continuació:
- QA, QB, QC i QD (pius núms. 14, 13, 12 i 11, respectivament): sortides del comptador. QA correspon al bit de menys pes.
- CLK (piu 2): entrada de rellotge actiu per flanc ascendent.
- VCC (piu 16): alimentació del circuit integrat (+5 V).
- GND (piu 8): connexió a massa del circuit integrat.
- A, B, C i D (pius núm. 3, 4, 5 i 6, respectivament): a aquest comptador li podem indicar per quin nombre ha de començar a comptar. Normalment serà el 0000, però amb les entrades A, B, C i D li podem indicar un altra combinació d’inici (A correspon al bit de menys pes)
 (piu núm. 9): quan s’aplica un nivell baix a l’entrada
(piu núm. 9): quan s’aplica un nivell baix a l’entrada  ,el comptador assumeix l’estat de les entrades A, B, C i D en el següent flanc ascendent de rellotge.
,el comptador assumeix l’estat de les entrades A, B, C i D en el següent flanc ascendent de rellotge. (piu núm. 1): entrada d’esborrat activa a nivell baix que posa a zero de manera síncrona (és a dir, en el següent flanc ascendent de rellotge) les quatre sortides del comptador.
(piu núm. 1): entrada d’esborrat activa a nivell baix que posa a zero de manera síncrona (és a dir, en el següent flanc ascendent de rellotge) les quatre sortides del comptador.- ENP i ENT (pius núm. 7 i 10, respectivament): entrades d’habilitació. Aquestes entrades han d’estar a nivell alt perquè el comptador pugui comptar. Quan almenys una de les dues entrades és a nivell baix, el comptador es desactiva.
- RCO (piu núm. 15): aquesta sortida es posa a nivell alt quan el comptador assoleix el valor 1111 a la seva sortida.
Registres de desplaçament
Els registres de desplaçament són una altra aplicació digital seqüencial que, com els comptadors, es poden obtenir mitjançant la connexió de diversos biestables o utilitzant circuits integrats específics.
Aplicacions dels registres de desplaçament
Les principals aplicacions dels registres de desplaçament són:
- emmagatzematge de dades,
- conversió de dades paral·lel/ sèrie,
- conversió de dades sèrie/ paral·lel,
- introducció de retards en els sistemes de comunicació.
Els registres de desplaçament són sistemes digitals seqüencials formats per biestables, que s’utilitzen per emmagatzemar i transferir dades digitals.
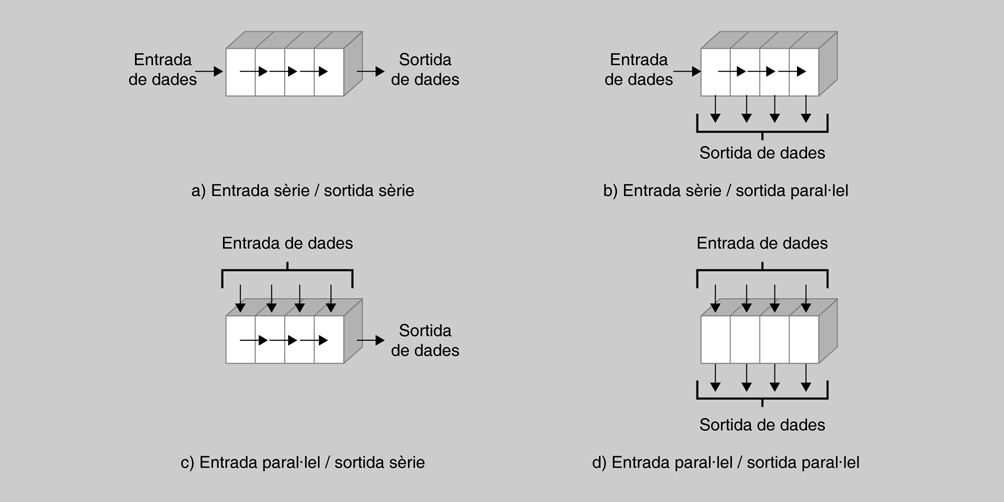
Els registres de desplaçament es poden classificar segons com s’introdueix la informació i de com s’obté aquesta informació. D’acord amb aquest criteri, podem trobar (figura):
- registres de desplaçament entrada sèrie/sortida sèrie
- registres de desplaçament entrada sèrie/sortida paral·lel
- registres de desplaçament entrada paral·lel/sortida sèrie
- registres de desplaçament entrada paral·lel/sortida paral·lel.
Registre de desplaçament amb entrada sèrie/sortida sèrie
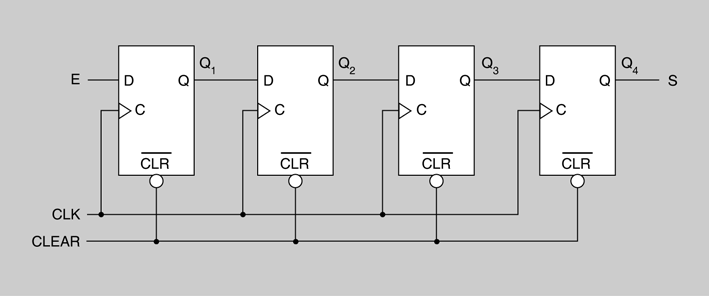
En la figura es mostra l’estructura d’un registre de desplaçament entrada sèrie/sortida sèrie de quatre bits, format per quatre flip-flops D amb senyal d’esborrat (CLR).
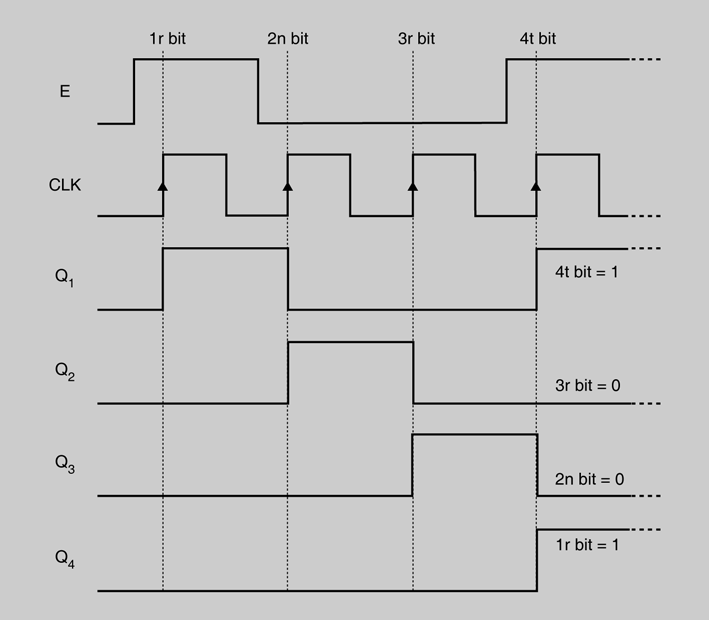
El funcionament d’aquest registre de desplaçament és ben senzill. Per l’entrada E es van introduint les dades. Cada bit dels introduïts serà desplaçat al següent flip-flop a cada flanc ascendent del senyal de rellotge, de manera que a partir del quart flanc ascendent la informació introduïda s’obtindrà a la sortida de manera successiva. En la figura es mostren els senyals E, CLK, Q1, Q2, Q3 i Q4 quan s’emmagatzema el codi 1001 en un registre de desplaçament sèrie/sèrie.
Estructura interna dels registres de desplaçament
La majoria dels registres de desplaçament es realitzen a partir de flip-flops tipus D.
Registre de desplaçament amb entrada sèrie/sortida paral·lel
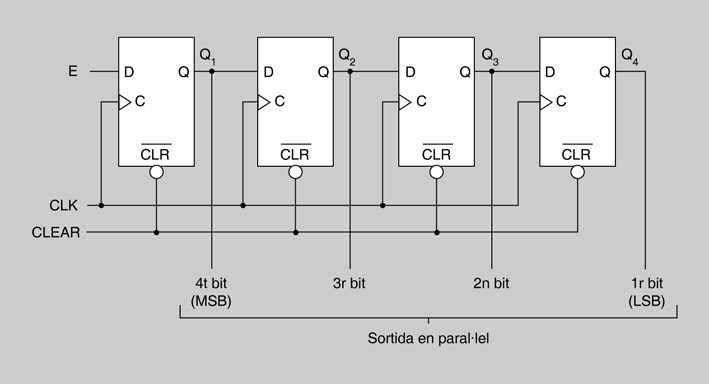
Es pot obtenir un registre de desplaçament d’entrada sèrie/sortida paral·lel partint de l’esquema del registre sèrie/sèrie. Només caldrà connectar les sortides paral·lel als punts Q1, Q2, Q3 i Q4 com es mostra en la figura. El funcionament d’aquest registre és el següent:
- Quan es produeix un flanc ascendent de CLK entra un bit per la línia E i es queda a Q1. En el mateix instant, el bit que era al punt Q1 passa a Q2, el que era a Q2 passa a Q3 i el que era a Q3 passa a Q4.
- La informació introduïda per l’entrada sèrie estarà disponible a les sortides Q1, Q2, Q3 i Q4 al flanc ascendent del quart pols de rellotge.
MSB i LSB
MSB vol dir Most Significant Bit, és a dir, el bit més significant, el de més pes.
LSB vol dir Least Significant Bit, és a dir, el bit menys significant, el de menys pes.
Registre de desplaçament universal
Un registre de desplaçament universal és un circuit integrat que incorpora els diferents modes de funcionament de registre, amb entrades i sortides sèrie i paral·lel.
-
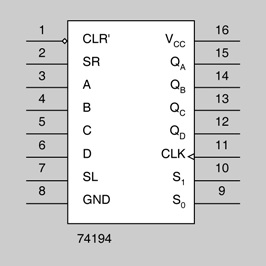
- 74194: registre de desplaçament universal
Un exemple clar de registre de desplaçament universal és el circuit integrat 74194.
La utilitat de cada piu d’aquest registre de desplaçament universal es descriu a continuació:
 (piu núm. 1): entrada asíncrona d’esborrat, activa a nivell baix.
(piu núm. 1): entrada asíncrona d’esborrat, activa a nivell baix.- S0 i S1 (pius núm. 9 i 10, respectivament): entrades de selecció del mode d’operació. Aquestes entrades actuen segons la taula.
- CLK (piu núm. 11): entrada de rellotge actiu per flanc ascendent.
- SR (piu núm. 2): entrada sèrie per fer desplaçaments a la dreta.
- SL (piu núm. 7): entrada sèrie per fer desplaçaments a l’esquerra.
- A, B, C i D (pius núm. 3, 4, 5 i 6, respectivament): entrades per fer càrregues en paral·lel.
- QA, QB, QC i QD (pius núm. 15, 14, 13 i 12, respectivament): sortides en paral·lel.
- VCC (piu 16): alimentació del circuit integrat (+5 V).
- GND (piu 8): connexió a massa del circuit integrat.
| S0 | S1 | Mode d’operació |
|---|---|---|
| 0 | 0 | Rellotge inhibit: no hi ha desplaçament |
| 0 | 1 | Desplaçament a l’esquerra |
| 1 | 0 | Desplaçament a la dreta |
| 1 | 1 | Càrrega en paral·lel de les dades a les sortides |
La càrrega en paral·lel es fa de manera síncrona, aplicant les dades a les entrades en paral·lel i posant les entrades de control de mode S0 i S1 a nivell alt. A partir d’aquest moment, les dades seran transferides a la sortida en el flanc ascendent del pols de rellotge; durant la càrrega en paral·lel, el flux de dades per l’entrada sèrie queda inhibit.