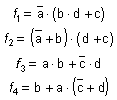Activitats

Sistemes analògics i sistemes digitals

L’objectiu d’aquesta activitat és aprendre a distingir entre senyals analògics i digitals.

Classifiqueu els següents aparells en analògics o digitals:

Termòmetre de mercuri
Disc dur d’ordinador
Cinta de casset
Disc de vinil
Disc compacte
Cinta de vídeo VHS
DVD
Càmera de fotos tipus rèflex
Reproductor MP3
Motor de corrent continu

Aparells analògics	Aparells digitals
Termòmetre de mercuri	Disc dur d’ordinador
Cinta de casset	Disc compacte
Disc de vinil	DVD
Cinta de vídeo VHS	Reproductor MP3
Càmera de fotos tipus rèflex
Motor de corrent continu

Sistemes binaris

L’objectiu d’aquesta activitat és reflexionar sobre les característiques bàsiques dels sistemes binaris.

Descriviu algun aparell o sistema que sigui binari, és a dir, que tingui només dos estats possibles.
Creieu que un polsador és un sistema binari? Per què?

Sistemes de numeració

L’objectiu d’aquesta activitat és practicar la conversió entre diferents sistemes de numeració.

Ompliu la següent taula amb les representacions de diversos nombres en diferents sistemes de numeració.

Decimal	Hexadecimal	Binari	BCD
	0x1B
45
		100101b
92			1001 0010
	0x99
		111111b
546
			1001 1001 1001
	0xABC

Decimal	Hexadecimal	Binari	BCD
27	0x1B	11011b	0010 0111
45	0x2D	101101b	0100 0101
37	0x25	100101b	0011 0111
92	0x5C	1011100b	1001 0010
153	0x99	10011001b	0001 0101 0011
63	0x3F	111111b	0110 0011
546	0x222	1000100010b	0101 0100 0110
999	0x3E7	1111100111b	1001 1001 1001
2748	0xABC	101010111100b	0010 0111 0100 1000

Suma en sistema binari

L’objectiu d’aquesta activitat és aprendre a sumar en binari.

Realitzeu les següents sumes en sistema binari:

Resta en sistema binari

L’objectiu d’aquesta activitat és aprendre a restar en binari.

Realitzeu les següents restes en sistema binari:

Primer calculem el complement a un del subtrahend: 1001.

A continuació calculem el complement a dos del subtrahend, sumant-li 1 al resultat anterior: 1010.

Finalment, sumem el minuend amb el complement a dos del subtrahend:

Per tant, el resultat de la resta 1011 – 0110 és 0101.

Primer calculem el complement a un del subtrahend: 011110.

A continuació calculem el complement a dos del subtrahend, sumant-li 1 al resultat anterior: 011111.

Finalment, sumem el minuend amb el complement a dos del subtrahend:

Per tant, el resultat de la resta 100111 – 100001 és 000110.

Primer calculem el complement a un del subtrahend: 110000.

A continuació calculem el complement a dos del subtrahend, sumant-li 1 al resultat anterior: 110001.

Finalment, sumem el minuend amb el complement a dos del subtrahend:

Per tant, el resultat de la resta 110011 – 001111 és 100100.

Avaluació de funcions lògiques

L’objectiu d’aquesta activitat és aprendre a avaluar funcions lògiques, seguint l’ordre correcte en el seu procés de resolució (parèntesis, negació, producte i suma).

Calculeu el valor que tenen les següents funcions quan a = 0, b = 1, c = 1 i d = 0.

Primera forma canònica d'una funció

L’objectiu d’aquesta activitat és aprendre a trobar l’expressió algebraica d’una funció a partir de la seva taula de veritat, utilitzant la suma de productes.

A partir de la següent taula de veritat, obteniu la primera forma canònica (suma de productes) de la funció f.

a	b	c	f
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

Pas 1. Primer ens fixem en les combinacions de valors que fan que la funció valgui 1:

a = 0, b = 0 i c = 1
a = 0, b = 1 i c = 0
a = 1, b = 0 i c = 1

Pas 2. Per cadascuna d’aquestes tres combinacions trobarem un terme producte, anomenat minterm.

En la primera combinació de valors, només la variable c està a nivell alt (a = 0, b = 0 i c = 1). Per tant, el minterm associat és:

En la segona combinació de valors, només la variable b està a nivell alt (a = 0, b = 1 i c = 0). Per tant, el minterm associat serà:

En la tercera combinació de valors, només la variable b està a zero (a = 1, b = 0 i c = 1). Per tant, el minterm associat serà:

Pas 3. Finalment, només cal fer la suma lògica dels tres minterms per obtenir la primera forma canònica de la funció:

Primera forma canònica d'una funció

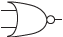
L’objectiu d’aquesta activitat és conèixer els símbols i l’expressió algebraica de les diferents portes lògiques.

Relacioneu els següents símbols de portes lògiques amb les seves expressions algebraiques.

Porta lògica	Expressió algebraica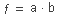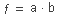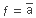