Principis bàsics de lògica digital
La lògica digital és la “manera de pensar i fer càlculs” que tenen totes les màquines digitals, que poden ser tant una senzilla calculadora com un autòmat programable o un potent ordinador. Per tant, per entendre com funcionen aquestes màquines digitals és necessari saber operar amb lògica digital.
A diferència dels sistemes analògics, els sistemes digitals només poden prendre un conjunt de valors discrets i canvien de valor per salts.
Els equips digitals utilitzen el sistema de numeració binari, el qual opera únicament amb dos dígits, el 0 i l’1. Com que els éssers humans pensem amb els sistema de numeració decimal, s’han desenvolupat tècniques matemàtiques per fer conversions entre sistemes de numeració: de binari a decimal, de decimal a binari, de binari a hexadecimal, d’hexadecimal a binari, de decimal a hexadecimal i d’hexadecimal a decimal.
Els sistemes digitals fan operacions matemàtiques amb dades expressades en binari. Com a instrument matemàtic per treballar amb sistemes digitals utilitzem l’àlgebra de Boole.
Senyals analògics i senyals digitals
Al camp de l’electricitat i l’electrònica, hi ha dues maneres de representar informació, que anomenem analògica i digital, i que es distingeixen per la naturalesa dels valors que poden prendre les variables que ens donen una mesura d’aquesta informació.
Un senyal analògic és aquell que varia de forma contínua (sense salts) i pot prendre infinits valors al llarg del temps.
-

- Termòmetre analògic de mercuri
Termòmetre de mercuri
El clàssic termòmetre de mercuri està format per un tub de vidre totalment tancat dins del qual hi ha un líquid, en la majoria dels casos mercuri o alcohol.
El principi de funcionament que permet a aquest instrument mesurar la temperatura és que el volum del líquid que conté canvia de manera uniforme segons la temperatura, de manera que quan el líquid s’escalfa s’expandeix i quan es refreda es contrau. Aquest canvi de volum és visible a través del vidre i es manifesta fent més llarga o més curta la columna de líquid que hi ha dins del tub.
En aquest cas, la informació és la temperatura i la variable que conté la informació és la columna del líquid. Com ja sabem, aquest instrument no és elèctric ni electrònic, però la naturalesa d’aquest senyal és clarament analògica, ja que la longitud de la columna de líquid canvia de manera contínua (sense salts) i pot prendre infinits valors (dins dels límits de l’escala del termòmetre).
Un senyal digital és aquell que només pot prendre un conjunt de valors discrets i canvia de valor per salts.
-

- Termòmetre digital
Termòmetre digital
Els termòmetres més moderns no es basen en el mètode clàssic del termòmetre de mercuri. Aquests instruments disposen d’una petita pantalla en la qual es visualitza un nombre que representa la temperatura mesurada.
En aquest cas, la informació també és la temperatura i la variable que conté la informació és el nombre que es veu a la pantalla.
Aquesta variable és digital, ja que el nombre mostrat a la pantalla no varia d’una manera contínua amb la temperatura, sinó que normalment canvia en salts discontinus o discrets de 0,1 graus.
Sistemes de numeració en els sistemes digitals
A la nostra vida quotidiana, els éssers humans treballem amb deu xifres (0, 1, 2, 3, 4, 5, 6, 7, 8 i 9) que combinem per representar qualsevol número i per fer càlculs: és el que s’anomena sistema de numeració decimal.
Els equips digitals (ordinadors, autòmats programables, etc.) treballen amb un mètode per comptar i fer càlculs molt particular: tan sols treballen amb les xifres 0 i 1. És el que s’anomena sistema de numeració binari.
Com que els nombres binaris poden ser molt llargs, sovint s’utilitzen altres sistemes de numeració per representar-los: són els sistemes de numeració hexadecimal i BCD
Per entendre com funcionen els equips digitals és necessari que sapigueu operar amb nombres binaris, hexadecimals i BCD, i que sapigueu convertir un nombre d’un sistema a un altre.
Sistema de numeració decimal
Sabíeu...
… que al llarg de la història han sorgit molts sistemes de numeració diferents? El nostre sistema decimal actual va ser inventat a l’Índia i transmès a Europa pels àrabs.
L’ésser humà fa servir la numeració decimal pel costum dels homes primitius de comptar amb els dits de la mà: d’aquesta manera era més fàcil fer la correspondència entre cada objecte i un dit de la mà.
Amb el temps, aquests homes primitius van haver de representar quantitats per escrit i va sorgir la necessitat d’assignar un símbol o dígit a cada nombre, fet que va originar els deu símbols (dígits) que es fan servir en el sistema decimal:
Dígit
Un dígit és cadascun dels signes o els símbols que s’empren en un determinat sistema de numeració per formar els diferents nombres.

Però, és clar, normalment volem representar més de deu nombres. Cap problema: sabem que el sistema decimal permet representar qualsevol nombre sencer afegint-hi noves xifres. Així, amb dues xifres decimals, podem representar 100 nombres (del 0 al 99), amb tres xifres podem representar 1.000 nombres (del 0 al 999) i així consecutivament.
Descomposició d'un nombre decimal
El nombre 2.364 consta de 4 xifres que representen el nombre d’unitats (4), desenes (6), centenes (3) i milers (2).
Si fem servir una mica de matemàtiques, podem descompondre aquest nombre tal com s’indica:

Una altra manera d’escriure la suma anterior és fent servir la potenciació:

Escrivint el nombre com una suma de potències, queda molt més clar per què el sistema decimal es diu que és un sistema en base deu: cada dígit multiplica la base (el 10) elevada a un exponent.
Recordeu aquesta manera de descompondre un nombre perquè us serà molt útil quan estudieu els sistemes binari i hexadecimal.
Sistema de numeració binari
El sistema de numeració binari també és anomenat sistema de numeració en base dos.
El sistema binari fa servir únicament dos dígits, el 0 i l’1, en lloc dels deu dígits que fa servir el sistema decimal.
Així, amb una xifra només podem representar dos nombres: el 0 i l’1. Per representar més de dos nombres hem d’afegir noves xifres a l’esquerra, tal com havíem fet en el cas decimal.
Cada una d’aquestes xifres és el que es coneix com a bit i , per tant, podem dir que un nombre binari es compon d’una sèrie de bits.
- Amb dos bits podem representar quatre nombres: 00, 01, 10 i 11.
- Amb tres bits podem representar vuit nombres: 000, 001, 010, 011, 100, 101, 110 i 111.
- Amb quatre bits podem representar setze nombres: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110 i 1111.
- I així consecutivament.
En la taula podeu veure l’equivalència entre els primers nombres dels sistemes decimal i binari.
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Binari | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 |
| Decimal | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Binari | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Hi ha una relació entre el nombre de bits que té un codi binari i la quantitat de nombres que es poden representar. Aquesta important relació és la següent:

On N és la quantitat de nombres que es poden representar amb n bits.
L’agrupació de vuit bits és tan utilitzada en electrònica i, sobretot, en informàtica, que rep un nom especial: byte.
Quants nombres podem representar amb vuit bits?
La resposta és 28 o, el que és el mateix, 256.
Com que el primer nombre és el 0 (00000000), l’últim que es podrà representar és el 255 (11111111).
Treballar amb nombres binaris de molts dígits no és gaire còmode i és fàcil que ens equivoquem, per exemple, quan hem de copiar un nombre d’un lloc a un altre en un exercici.
De quatre bits en quatre bits
Per què s’acostumen a agrupar els nombres grans en quatre bits? Com veureu més endavant, agrupar d’aquesta manera un nombre binari ens facilitarà la tasca de convertir-lo a hexadecimal en el cas que sigui necessari.
Una manera d’intentar fer més llegible els nombres binaris consisteix a separar els nombres grans en grups de quatre bits començant per la dreta.
Per exemple, un nombre tan poc llegible com

es podria escriure de la manera següent:

En qualsevol cas, recordeu que el truc de separar en grups de quatre no és obligatori. Tan sols és una recomanació per facilitar-vos la tasca de treballar amb nombres binaris.
Fixeu-vos que, en aquest cas, el grup situat més a l’esquerra no té quatre bits sinó dos. Si voleu, podeu representar aquest grup amb quatre bits afegint a l’esquerra els 0 que calguin:

Indicació de nombre binari
De vegades, s’afegeix el subíndex 2 per indicar que un nombre està expressat en binari. Per exemple, el nombre binari 101 s’escriu 1012. També es pot indicar que un nombre és binari amb el sufix b. Per exemple, el nombre binari 101 s’escriu 101b.
Sistema de numeració hexadecimal
El sistema de numeració hexadecimal utilitza setze dígits:

El mecanisme que es fa servir per construir nombres és similar al que hem vist en el sistema decimal i binari:
El sistema de numeració hexadecimal també és anomenat sistema de numeració en base setze.
- Amb una xifra podem representar 16 nombres: del 0 al F. Per representar més de 16 nombres, l’únic que hem de fer és afegir noves xifres hexadecimals a l’esquerra.
- Amb dues xifres podem representar 256 nombres: 00, 01, 02, …, 0F, 10, 11, 12, …, 1F, 20, 21, … 2F, … …, F0, F1, F2, … FF
- Amb tres xifres podem representar 4.096 nombres: 000, 001, …, 00F, 010, …, 0F0, 0F1, 0FF, …, FFA, FFB, …, FFF
- I així consecutivament.
A la taula es representen els primers nombres decimals i la seva correspondència en hexadecimal.
Indicació de nombre hexadecimal
De vegades, s’afegeix el prefix 0x per indicar que un nombre està expressat en hexadecimal. Per exemple, el nombre hexadecimal 13 s’escriu 0x13. També es pot indicar que un nombre és hexadecimal amb el sufix H. Per exemple, el nombre hexadecimal 13 s’escriu 13H.
| Repr. decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Repr. hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Repr. decimal | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Repr. hexadecimal | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
Conversió entre sistemes de numeració
Els sistemes digitals treballen amb el sistema de numeració binari, però els éssers humans pensem amb el sistema de numeració decimal. Per tant, es fa necessari saber convertir nombres binaris en decimals i a l’inrevés.
El sistema de numeració hexadecimal s’utilitza per representar nombres binaris d’una manera més compacta. També es necessari saber convertir nombres hexadecimals al sistema binari i decimal i a l’inrevés.
Per fer totes aquestes conversions s’utilitzen unes tècniques matemàtiques molt senzilles.
Conversió de binari a decimal
Per convertir un nombre binari a decimal s’ha de fer una suma de termes en els quals cada dígit binari multiplica el nombre 2 elevat a un exponent.
Per exemple, l’equivalent decimal del nombre binari 1101012 es pot calcular de la manera següent:

Podem eliminar els termes que multipliquen per zero:

Ara només cal substituir cada potència pel seu valor decimal (25 = 32, 24 = 16, 22 = 4 i 20 = 1) i fer la suma de tots els termes:

Ja hem acabat! El nombre binari 1101012 és el nombre decimal 53.
Aquest problema es pot resoldre gràficament, mitjançant una taula com la mostrada a la taula. A la part superior de la taula apareix l’equivalent decimal de les diferents posicions dels dígits binaris (d’esquerra a dreta, des de 27 fins a 20).
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
A la taula, hi escriurem de dreta a esquerra el nombre binari i després sumar els valors decimals de les caselles que estiguin a 1.
Per exemple, el número binari 10001100 es faria com es mostra a la taula.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Sumem els termes a 1, obtenint:

Conversió de decimal a binari
Un mètode gràfic per convertir un nombre binari a decimal utilitza una taula com la mostrada a la taula. A la part superior de la taula apareix l’equivalent decimal de les diferents posicions dels dígits binaris (d’esquerra a dreta, des de 27 fins a 20).
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
Per convertir a decimal, únicament calia posar el nombre binari sobre la plantilla, escriure’l de dreta a esquerra i sumar els valors que siguin a 1.
La qüestió que ens ocupa ara és la contrària: a partir del nombre decimal volem obtenir l’equivalent binari. Per fer això, anirem omplint la fila inferior de la plantilla d’esquerra a dreta amb uns o zeros, comptant fins a arribar al nombre decimal desitjat.
Per exemple, volem trobar l’equivalent binari del nombre decimal 89. Utilitzant la plantilla obtindrem el mostrat a la taula.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
El raonament que hem seguit per omplir la plantilla és el següent:
- Comencem per la cel·la de més a l’esquerra (la de pes 128). Posem la cel·la a 0 perquè si la poséssim a 1, el nombre decimal obtingut seria, com a mínim, el 128 i ens passaríem de 89.
- Continuem amb la següent cel·la a la dreta (la de pes 64). Aquesta la posem a 1 perquè amb 64 encara no arribem a 89.
- Continuem amb la següent cel·la a la dreta (la de 32). Aquesta la posem a 0 perquè si la poséssim a 1, tindríem 64 + 32 = 96 i ens passaríem de 89.
- Continuem amb la següent cel·la a la dreta (la de pes 16). Aquesta la posem a 1 perquè així tenim 64 + 16 = 80 i encara no arribem a 89.
- Continuem amb la següent cel·la a la dreta (la de pes 8). Aquesta la posem a 1 perquè així tenim 64 + 16 + 8 = 88 i encara no arribem a 89.
- Continuem amb la següent cel·la a la dreta (la de pes 4). Aquesta la posem a 0 perquè si la poséssim a 1, tindríem 64 + 16 + 8 + 4 = 92 i ens passaríem de 89.
- Continuem amb la següent cel·la a la dreta (la de pes 2). Aquesta la posem a 0 perquè si la poséssim a 1, tindríem 64 + 16 + 8 + 2 = 90 i ens passaríem de 89.
- Continuem amb la següent cel·la a la dreta (la de pes 1). Aquesta la posem a 1 perquè així tenim 64 + 16 + 8 + 1 = 89 i obtenim el valor decimal desitjat.
Per tant, el nombre binari equivalent al decimal 89 és el 0101 10012.
Conversió de binari a hexadecimal
Passar un nombre binari al seu equivalent hexadecimal és molt fàcil, perquè cada dígit hexadecimal es codifica directament amb quatre dígits binaris.
Amb un nombre binari qualsevol, només cal fer grups de quatre bits començant per la dreta del nombre binari.
Cadascun d’aquests grups es correspondrà amb un símbol del sistema hexadecimal, de manera que la seqüència ordenada d’aquests símbols és l’equivalent hexadecimal del nombre binari.
Fixeu-vos que aquest mètode és aplicable a qualsevol nombre binari, independentment del nombre de bits que tingui.
Per a la vostra referència, en la taula teniu les equivalències entre els 16 primers nombres dels sistemes de numeració decimal, binari i hexadecimal.
| Decimal | Binari | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Quin nombre hexadecimal és el nombre binari 1010 001 1110 1001?
En primer lloc hem de fer grups de quatre bits començant per la dreta, tal com es mostra en la figura següent:
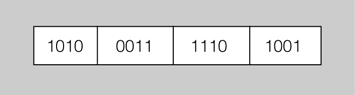
Seguidament, “traduïm” cada grup de quatre bits al seu equivalent hexadecimal (figura següent), segons la correspondència que es mostra a la taula.
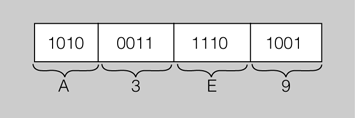
Per tant, l’equivalent hexadecimal del nombre binari 1010 0011 1110 10012 és el 0xA3E9
Conversió d'hexadecimal a binari
En un nombre hexadecimal qualsevol, cada dígit es correspondrà amb un grup de quatre bits, de manera que la seqüència ordenada d’aquests bits és l’equivalent binari del nombre hexadecimal
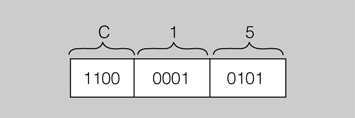
Quin nombre binari és el nombre hexadecimal 0xC15?
Únicament cal identificar el grup de quatre bits associat a cada dígit hexadecimal, com es mostra a la figura següent. Per tant, el nombre hexadecimal 0xC15 és el nombre binari 1100 0001 0101.
Conversió de decimal a hexadecimal
El mètode per convertir un nombre decimal a hexadecimal consisteix a fer dues senzilles accions: en primer lloc es converteix el nombre decimal a binari i, seguidament, es converteix el nombre binari resultant a hexadecimal.
Quin nombre hexadecimal és el 206 decimal?
Primer convertirem el nombre decimal 206 a nombre binari, mitjançant el mètode gràfic, obtenint el número binari 11001110.
A continuació convertim aquest nombre binari a hexadecimal, fent grups de quatre bits i convertint-los al símbol hexadecimal corresponent (figura següent):
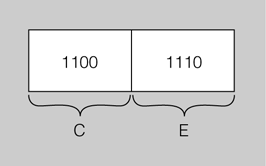
Per tant, l’equivalent hexadecimal del nombre decimal 206 és el 0xCE.
Conversió d'hexadecimal a decimal
Recordeu que el sistema hexadecimal també s’anomena sistema de base setze i, per tant la posició de cada dígit anirà referida a una potència de 16.
Per convertir un nombre hexadecimal a decimal s’ha de fer una suma de termes en els quals cada dígit hexadecimal multiplica el nombre 16 elevat a un exponent.
Per exemple, l’equivalent decimal del nombre 0x1B2 es calcula així:
Recordeu que el prefix 0x indica que el nombre està expressat en hexadecimal.

Fet això, només ens cal un pas més per passar a decimal: substituir els símbols A, B, C, D, E i F pel seu equivalent decimal (en la taula podeu consultar aquestes equivalències) i operar fins a obtenir un nombre decimal:

El dígit B correspon al nombre decimal 11. Ara només cal substituir cada potència pel seu valor decimal (162 = 256, 161 = 16 i 160 = 1) i fer la suma de tots els termes:

Ja hem acabat! El nombre hexadecimal 0x1B2 és el nombre 434 en decimal
Altres formes de codificar nombres sencers
Hi ha diferents sistemes per codificar els valors numèrics. Els més utilitzats són els sistemes de numeració decimal, binari i hexadecimal.
Ara bé, els sistemes digitals fan servir altres codificacions, per exemple, per assignar un codi que representi una lletra de l’abecedari o bé que indiqui la posició de l’eix d’un motor.
En casos com aquests es fan servir uns codis dissenyats especialment per satisfer aquestes i altres necessitats. Un d’aquests codis és el BCD, el qual s’utilitza molt en el món dels autòmats programables.
Codificació BCD
La sigla BCD prové de l’anglès: Binary Coded Decimal, és a dir, decimal codificat en binari.
Per passar un nombre decimal al seu equivalent BCD només cal passar cada xifra del nombre decimal al seu equivalent en binari en quatre bits, independentment.
Cada xifra del número decimal generarà quatre dígits binaris.
Per exemple, el nombre decimal 9285 seria el nombre 1001 0010 1000 0101 en codi BCD, ja que:
- El 9 és el nombre 1001 en binari.
- El 2 és el nombre 0010 en binari.
- El 8 és el nombre 1000 en binari.
- El 5 és el nombre 0101 en binari.
Fixeu-vos que per representar cada símbol d’un nombre decimal sempre s’utilitzen quatre bits en codi BCD.
Aritmètica binària
Les operacions es realitzen de la mateixa forma que en sistema decimal, però, a causa de la senzillesa del sistema binari, es poden fer algunes simplificacions.
Els sistemes digitals (ordinadors, calculadores, autòmats programables…) són capaços de fer operacions aritmètiques amb dades expressades en sistema binari.
Suma en sistema binari
Les possibles combinacions de la suma binària són:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0, i en porto una
Les tres primeres combinacions són evidents. Però la suma d’1+1, que en decimal sabem que és 2, s’ha d’escriure en binari amb dos dígits (10). Per tant, la suma d’1+1 és 0 i s’arrossega una unitat que se suma a la següent posició a l’esquerra.
Quin és el resultat de sumar els nombres binaris 1011 i 0110?
Fent la suma segons les regles de la suma binària obtenim:

Podeu observar que el resultat té cinc dígits perquè arrosseguem un 1.
La mateixa operació però en sistema decimal hauria estat: 11 + 6 = 17.
Complement a un i complement a dos d'un nombre binari
El complement a un i el complement a dos són dues eines matemàtiques que faciliten molt les tasques aritmètiques en el sistema binari, sobretot la realització de restes i el treball amb nombres negatius.
Complement a un d'un nombre binari
El complement a un (C1) d’un nombre binari és el nombre resultant d’invertir els uns i els zeros d’aquest nombre.
Per exemple, el complement a un del nombre 1101 és el nombre 0010.
Complement a dos d'un nombre binari
El complement a dos (C2) d’un nombre binari és el nombre resultant de sumar 1 al seu complement a un. És a dir, C2 = C1 + 1.
Per exemple, per calcular el complement a dos del nombre binari 1001 primer calculem el seu complement a un invertint uns i zeros. Ens dóna el nombre 0110. A aquest complement a un li sumem una unitat i ja tenim el complement a dos: 0110 + 1 = 0111.
Generalment s’assumeix que el C2 és la manera de representar el negatiu d’un número binari.
Resta en sistema binari
Recordeu...
… que en una resta de dos nombres A - B, el nombre A s’anomena minuend i el nombre B s’anomena subtrahend.
La resta de dos nombres binaris pot obtenir-se sumant al minuend el complement a dos del subtrahend.
Per exemple, fem la resta 1011011 - 0101110:
- Primer calculem el complement a un del subtrahend:1010001.
- A continuació calculem el complement a dos d’aquest: 1010010.
- Finalment sumem el minuend amb el complement a dos del subtrahend.

Podeu comprovar que si “traduïm” la resta binària 1011011 - 0101110 = 0101101 a decimal ens dóna: 91 46 = 45.
En el resultat de la suma ens sobra un bit, ja que arrosseguem un 1 per l’esquerra. Però com que el nombre resultant de la resta no pot ser més gran que el minuend, el bit sobrant s’ignora. Per tant: 1011011 - 0101110 = 0101101.
Representació de nombres negatius en sistema binari
Amb el sistema decimal, els nombres negatius es representen senzillament precedint-los amb el signe -. En canvi, en el sistema binari no s’utilitza el signe sinó que es fan servir altres mètodes. El mètode més utilitzat és el del complement a 2 (C2).
Altres representacions de nombres negatius binaris
Hi ha altres mètodes per representar nombres negatius en sistema binari (el mètode de signe i magnitud, el mètode de complement a un, el mètode d’excés N…), però no són tan utilitzats com el mètode de complement a dos.
Els nombres positius es representen amb el sistema de numeració binari normal, i els nombres negatius es representen amb el sistema de numeració binari en complement a dos.
En la taula es mostra la representació binària des del -128 fins al +127. Si us hi fixeu, el bit de més pes sempre és zero per als nombres positius i sempre és u per als nombres negatius. Aquest bit de més pes s’anomena bit de signe, perquè ens indica si el nombre és positiu (bit de signe a zero) o negatiu (bit de signe a un). La resta de bits s’anomenen magnitud.
| Decimal | Signe | Magnitud | Codi |
|---|---|---|---|
| +127 | 0 | 111 1111 | Natural |
| +126 | 0 | 111 1110 | Natural |
| +125 | 0 | 111 1101 | Natural |
| +124 | 0 | 111 1100 | Natural |
| … | 0 | … | Natural |
| +5 | 0 | 000 0101 | Natural |
| +4 | 0 | 000 0100 | Natural |
| +3 | 0 | 000 0011 | Natural |
| +2 | 0 | 000 0010 | Natural |
| +1 | 0 | 000 0001 | Natural |
| 0 | 0 | 000 0000 | Natural |
| -1 | 1 | 111 1111 | C2 |
| -2 | 1 | 111 1110 | C2 |
| -3 | 1 | 111 1101 | C2 |
| -4 | 1 | 111 1100 | C2 |
| -5 | 1 | 111 1011 | C2 |
| … | 1 | … | C2 |
| -125 | 1 | 000 0011 | C2 |
| -126 | 1 | 000 0010 | C2 |
| -127 | 1 | 000 0001 | C2 |
| -128 | 1 | 000 0000 | C2 |
Àlgebra de Boole
L’àlgebra de Boole es basa en el següent:
- Un conjunt d’elements que únicament poden tenir dos valors possibles i que anomenarem 0 i 1.
- Tres operacions que anomenarem suma lògica, producte lògic i negació.
George Boole (1815-1864)
Matemàtic i filòsof britànic. Va desenvolupar l’anomenada àlgebra de Boole com una eina per analitzar la ment humana. L’aplicació als sistemes digitals va ser posterior.
Un element qualsevol de l’àlgebra de Boole es representa amb una lletra que s’anomena variable booleana o, alternativament, variable binària. Així, doncs, cada variable binària té associat un valor 1 o un valor 0.
L’àlgebra de Boole és una eina matemàtica que ens permet treballar amb sistemes que només fan servir dos estats clarament diferenciats, com és el cas dels sistemes digitals.
Què significa 1 i què significa 0?
Això depèn de l’aplicació i l’únic important és que representa dos estats clarament diferenciats.
Vegem-ne un exemple senzill: molts cotxes incorporen un sistema que informa de l’estat de les portes, de manera que encén un llum indicador si detecta que hi ha una porta oberta.
Com que cadascuna de les portes del vehicle únicament poden estar en dos estats diferents (porta oberta o porta tancada), podem “traduir” aquesta situació a l’àlgebra de Boole d’una manera molt clara.
Per exemple, podríem associar una variable binària a cada porta que anomenarem de la següent manera:
- A: variable que representa l’estat de la porta del conductor
- B: variable que representa l’estat de la porta del copilot
- C: variable que representa l’estat de la porta del darrere esquerra
- D: variable que representa l’estat de la porta del darrere dreta
I finalment, associaríem a l’estat “porta oberta” el valor 1 i a l’estat “porta tancada”, el valor 0. Òbviament, aquesta elecció ha estat arbitrària i podríem haver fet l’assignació contrària.
Fixeu-vos que amb aquests simples passos hem pogut traduir una informació del món real al món matemàtic de l’àlgebra de Boole, de tal manera que si ara ens diguessin:
- A = 1
- B = 1
- C = 0
- D = 0
sabríem que les dues portes davanteres del nostre vehicle estan obertes i les dues del darrere, tancades.
Variables binàries al món real
Hi ha molts casos del món real que es poden “traduir” al món binari d’uns i zeros. Per exemple, l’estat de les portes d’un vehicle: cada porta del vehicle equival a una variable binària, de manera que si la porta està oberta la variable pren el valor 1 i si la porta està tancada la variable pren el valor 0.
Les tres operacions bàsiques de l’àlgebra de Boole són les següents:
- Suma lògica. És representada pel signe + i requereix dos operands. Aquesta operació queda definida en la taula.
| a | b | a + b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
El resultat de la suma lògica és 1 si qualsevol dels operands és 1.
- Producte lògic. És representat pel signe · i requereix dos operands. Aquesta operació queda definida en la taula.
| a | b |  |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
El resultat del producte lògic és 1 només si tots els operands són 1.
- Negació. És una operació que només requereix un operand. Si l’operand és la variable a, una línia horitzontal sobre aquesta variable indica que està negada o complementada (
 ). Aquesta operació queda definida en la taula.
). Aquesta operació queda definida en la taula.
| a |  |
|---|---|
| 0 | 1 |
| 1 | 0 |
L’àlgebra de Boole és el suport matemàtic per al disseny i l’anàlisi dels sistemes digitals i, com tota àlgebra, disposa d’una sèrie de postulats i teoremes. Segurament les més importants són el teorema d’absorció, molt útil en simplificacions, i el teorema de DeMorgan, el qual ens indica com es converteix un producte lògic en una suma lògica i a l’inrevés.
El teorema d’absorció es pot expressar amb aquestes dues expressions algebraiques:

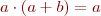
El teorema de DeMorgan es pot expressar amb aquestes dues expressions algebraiques:


Funcions lògiques
Diferents maneres d'escriure una funció lògica
En alguns llibres veureu que, al costat del nom de la funció, s’acostuma a escriure entre parèntesis les variables emprades per la funció. Per exemple:

Tanmateix, moltes vegades veureu que el signe · del producte lògic no s’escriu, ja que es dóna per suposada la seva existència. Per exemple, la funció anterior es pot escriure així:

Anomenem funció lògica una variable binària que pren el valor d’una expressió algebraica formada per altres variables binàries relacionades de la manera que sigui mitjançant les operacions suma lògica, producte lògic i negació.
Per exemple, les següents expressions són funcions lògiques definides per una expressió algebraica:


Diem que una funció està expressada com una suma de productes si la seva expressió algebraica està formada per una suma de termes i cada terme està format per unes variables que es multipliquen entre elles.
Per exemple, la funció següent és una suma de productes:

Diem que una funció està expressada com un producte de sumes si la seva expressió algebraica està formada per un producte de termes i cada terme està format per unes variables que se sumen entre elles.
Compte amb els parèntesis!
Pareu atenció que, en el cas dels productes de sumes, és obligatori l’ús de parèntesis en els termes, ja que primer s’han d’avaluar les sumes i després el producte. Si, per error, escrivíssim la funció de l’exemple així:

entendríem que primer s’hauria de fer el producte  i després fer la suma de tots els termes (estaríem al davant d’una funció en forma de suma de productes)
i després fer la suma de tots els termes (estaríem al davant d’una funció en forma de suma de productes)
Per exemple, la funció següent és un producte de sumes:

Com s'avaluen les funcions lògiques?
Donada una expressió algebraica booleana formada per molts termes, hauríem de trobar el valor resultant de la funció seguint aquest ordre:
- Parèntesis
- Operació de negació
- Operació producte lògic
- Operació suma lògica
Exemple d'avaluació de funció lògica
Volem saber quin valor té la funció  quan a = 0, b = 1, c = 1 i d = 1.
quan a = 0, b = 1, c = 1 i d = 1.
Solució
S’hauria d’avaluar seguint els següents passos:
Com que no hi ha parèntesis ni negacions, en primer lloc es farien les operacions de producte lògic:

Per acabar, es faria la suma lògica dels resultats anteriors. En aquest cas, substituïm a · b pel seu valor (0) i c · d pel seu valor (1), i obtindrem:

Exemple d'avaluació de funció lògica
Volem saber quin valor té la funció  quan a = 1, b = 1 i c = 1.
quan a = 1, b = 1 i c = 1.
En aquest cas, en primer lloc s’ha de fer l’operació que hi ha dins del parèntesi:

Després s’ha de fer l’operació de negació que té la variable a:

I finalment s’ha de fer el producte lògic d’aquests dos resultats:

Taula de veritat d'una funció lògica
Una taula de veritat és una manera de representar una funció lògica, en la qual es mostra el valor que pren la funció per a cadascuna de les combinacions de les variables d’entrada de la funció.
Per construir la taula de veritat d’una funció lògica s’han de seguir els següents passos:
- Dibuixar una taula amb:
- tantes columnes com variables tingui la funció, més una columna addicional
- tantes files com el nombre de possibles combinacions de les variables d’entrada, més una fila addicional
- En la fila superior es posen els noms de les variables (en les columnes de l’esquerra) i de la funció (en la columna de la dreta).
- S’omple la resta de files amb les diferents combinacions de valors de les variables d’entrada, en ordre creixent, com si comptéssim en binari natural.
- S’omple la columna de la dreta amb el valor que pren la funció per a cada combinació de valors d’entrada.
Recordeu el que heu après al subapartat “Sistema de numeració binari”: si tenim n variables, podem fer 2n combinacions diferents.
Exemple: taula de veritat de la funció $f_1=a\cdot \overline{c}+b$
Per construir la taula de veritat de la funció  faríem el següent:
faríem el següent:
- Construïm la taula:
- Amb 3 + 1 (és a dir, 4) columnes, ja que la funció és de tres variables (a, b i c).
- Amb 23 + 1 (és a dir, 9) files, ja que amb 3 variables es poden fer 23 = 8 combinacions.
- Posem el nom de les variables (a, b, c) i de la funció (f1) a la fila superior.
- Omplim a sota totes les combinacions de valors que podem tenir amb tres variables. La primera combinació és 000, la següent 001, la següent 010… fins a arribar a l’última combinació 111 (com si comptéssim en binari).
- Avaluem la funció per a cadascuna d’aquestes combinacions i posem el resultat a la columna de la dreta.
El resultat obtingut es mostra a la taula.

| a | b | c |  |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Funcions equivalents
Una funció booleana es pot definir indistintament amb una expressió algebraica o amb una taula de veritat. Coneixem el mètode per trobar la taula de veritat d’una funció expressada algebraicament.
El que encara no hem vist és com es fa el pas invers: partir de la taula de veritat d’una funció i trobar una expressió algebraica que descrigui la mateixa funció. Això és el que estudiarem en l’apartat “Formes canòniques d’una funció”.
Abans, però, ens podríem plantejar si hi ha més d’una expressió algebraica que verifiqui una taula de veritat donada. I, efectivament, és això.
Expressions algebraiques aparentment diferents poden descriure la mateixa funció lògica. Quan passa això diem que les funcions són equivalents.
La manera més fàcil de descobrir si dues funcions són equivalents és trobar la taula de veritat a partir de cadascuna de les expressions algebraiques i comprovar si donen el mateix resultat.
Com a exemple, veurem si són equivalents les funcions següents:

Primer omplim la taula de veritat de  : el resultat el podeu veure a la taula.
: el resultat el podeu veure a la taula.

| a | b |  |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
A continuació omplim la taula de veritat de  : el resultat el podeu veure a la taula.
: el resultat el podeu veure a la taula.

| a | b |  |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Observant les dues taules, veiem que els resultats de les dues funcions són idèntics. Per tant,  i
i  són equivalents.
són equivalents.
Formes canòniques d'una funció
A continuació veurem com podem trobar una expressió algebraica d’una funció a partir de la seva taula de veritat. Hi ha dues maneres de fer-ho i es coneixen com a formes canòniques.
Primera forma canònica
La primera forma canònica es basa a expressar la funció com una suma de productes que deduirem de la taula de veritat mitjançant el procediment que utilitzem en l’exemple següent:
- A la taula de veritat, ens fixarem en les combinacions de valors de les variables d’entrada que fan que la funció valgui 1.
- Per cadascuna d’aquestes combinacions hem de trobar un terme producte, anomenat minterm, amb les següents característiques:
- Està format per totes les variables de la funció, negades o no.
- Aquestes variables estan multiplicades.
- Per saber si la variable ha d’estar negada o no a cada minterm, us heu de fixar en la combinació de valors:
- Si el valor d’aquesta variable és 0, aquesta variable haurà d’anar negada en el terme producte.
- Si el valor d’aquesta variable és 1, aquesta variable haurà d’anar directa (no negada) en el terme producte.
- Finalment, la primera forma canònica s’obté sumant tots els minterms.
| a | b | c | f |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Exemple: obtenció de la primera forma canònica d'una funció
A partir de la taula de veritat mostrada en la taula, trobarem la primera forma canònica de la funció.
Seguint el procediment descrit anteriorment:
- Primer ens fixem en les combinacions de valors que fan que la funció valgui 1:
- a = 0, b = 0 i c = 0
- a = 0, b = 1 i c = 1
- a = 1, b = 0 i c = 1
- Per a cadascuna d’aquestes tres combinacions trobarem un terme producte, anomenat minterm. Total, 3 termes.
- Cadascuna de les tres combinacions genera el minterm associat:
- En la primera combinació de valors, totes les variables estan a zero (a = 0, b = 0 i c = 0) i, per tant, aquestes variables estaran invertides en el minterm associat:
 .
. - En la segona combinació de valors, només la variable a està a zero (a = 0, b = 1 i c = 1). Per tant, el minterm associat serà:
 .
. - En la tercera combinació de valors, només la variable b està a zero (a = 1, b = 0 i c = 1). Per tant, el minterm associat serà:
 .
.
- Finalment, només cal fer la suma lògica dels tres minterms per obtenir la primera forma canònica de la funció:

Segona forma canònica
La segona forma canònica es basa a expressar la funció com un producte de sumes que deduirem de la taula de veritat mitjançant el següent procediment:
- A la taula de veritat, ens fixarem en les combinacions de valors de les variables d’entrada que fan que la funció valgui 0.
- Per cadascuna d’aquestes combinacions hem de trobar un terme producte, anomenat maxterm, amb les següents característiques:
- Està format per totes les variables de la funció, negades o no.
- Aquestes variables estan sumades.
- Per saber si la variable ha d’estar negada o no a cada maxterm, us heu de fixar en la combinació de valors:
- Si el valor d’aquesta variable és 0, aquesta variable haurà d’anar directa (no negada) en el terme suma.
- Si el valor d’aquesta variable és 1, aquesta variable haurà d’anar negada en el terme suma.
- Finalment, la segona forma canònica s’obté multiplicant tots els maxterms.
Recordeu que cal usar els parèntesis si es vol expressar correctament la funció com un producte de sumes.
Exemple: obtenció de la segona forma canònica d'una funció
A partir de la taula de veritat mostrada en la taula, trobarem la segona forma canònica de la funció.
Seguint el procediment descrit anteriorment:
- Primer ens fixem en les combinacions de valors que fan que la funció valgui 0:
- a = 0, b = 0 i c = 1
- a = 0, b = 1 i c = 0
- a = 1, b = 0 i c = 0
- a = 1, b = 1 i c = 0
- a = 1, b = 1 i c = 1
- Per a cadascuna d’aquestes cinc combinacions trobarem un maxterm o terme producte.
- Els maxterms que corresponen a cada combinació són els següents:
- A la combinació a = 0, b = 0 i c = 1 li correspon

- A la combinació a = 0, b = 1 i c = 0 li correspon

- A la combinació a = 1, b = 0 i c = 0 li correspon

- A la combinació a = 1, b = 1 i c = 0 li correspon

- A la combinació a = 1, b = 1 i c = 1 li correspon

- Finalment, només cal fer el producte lògic dels cinc maxterms per obtenir la segona forma canònica de la funció:

Portes lògiques bàsiques
Les portes lògiques...
… són per als sistemes digitals com els maons per a l’arquitectura: malgrat la seva senzillesa, ens permeten construir estructures molt complexes.
Fins i tot els sistemes digitals més complexos estan formats per blocs més petits encarregats de fer operacions senzilles amb senyals binaris. Aquests blocs fonamentals són el que coneixem com a portes lògiques.
Símbols de les portes
Les portes lògiques més importants disposen de símbols gràfics especials que les representen. Hi ha dues maneres de representar cada porta. Les normes que regulen aquestes dues simbologies són les següents:
- La norma IEEE 91-1973, que va ser la primera i més popular.
- La norma IEEE 91-1984, que és més recent i proporciona informació més precisa, encara que no s’utilitza tan sovint.
Cada porta lògica fa una funció determinada; de totes les possibles funcions existents, les portes lògiques bàsiques són aquelles que es constitueixen com a bons elements de disseny de propòsit general. Les portes lògiques bàsiques són la porta AND, la porta OR , la porta NOT, la porta NAND i la porta NOR.
Porta AND
La porta AND fa la funció de producte lògic i rep el nom de la paraula anglesa and, que significa i en català.
La sortida d’una porta AND és 1 només si totes les variables d’entrada són 1.
La figura mostra el símbols d’una porta AND de dues entrades, però els mateixos símbols serveixen per a un nombre d’entrades més gran, només cal afegir les connexions d’entrada necessàries al símbol.
IEEE és la sigla en anglès de l’Institut d’Enginyers en Electricitat i Electrònica. En català s’acostuma a pronunciar com aI E cub.

La funció que realitza la porta AND és anàloga a la funció que realitzen dos interruptors en sèrie.
Com podeu veure en la figura, la làmpada X1 tan sols s’encén (és a dir, la sortida es posa a estat 1 lògic) quan els interruptors A i B estan tancats (és a dir, quan les dues entrades estan a 1 lògic).
Porta OR
La porta OR realitza la funció suma lògica i rep el nom de la paraula anglesa or, que significa o en català.
La sortida d’una porta OR és 1 si, com a mínim, una variable d’entrada és 1.
La figura mostra el símbols d’una porta OR de dues entrades, la seva expressió algebraica i la seva taula de veritat.

La funció que realitza la porta OR és anàloga a la funció que realitzen dos interruptors en paral·lel.
Com podeu veure en la figura, la làmpada X2 s’encén (és a dir, la sortida es posa a estat 1 lògic) quan, com a mínim, un dels dos interruptors A i B està tancat.
Porta NOT
Aquesta porta, també coneguda com a inversor, només té una entrada i realitza la funció de negació, de manera que la sortida és 1 si l’entrada és 0 i la sortida és 0 si l’entrada és 1.
La figura mostra els símbols d’una porta NOT, la seva expressió algebraica i la seva taula de veritat.
Porta NAND
El nom d’aquesta porta prové de la unió de les paraules angleses notiand i, com el seu nom indica, és una porta AND amb la sortida invertida.
La sortida d’una porta NAND és 0 només si totes les variables d’entrada són 1.
La figura mostra els símbols d’una porta NAND, la seva expressió algebraica i la seva taula de veritat.
Porta NOR
La sortida d’una porta NOR és la invertida d’una porta OR. El seu nom prové de la unió de les paraules angleses noti or.
La sortida d’una porta NOR és 1 només si totes les variables d’entrada són 0.
La figura mostra els símbols d’una porta NOR, la seva expressió algebraica i la seva taula de veritat.
Porta XOR
També anomenada porta OR-exclusiva. La seva sortida és 1 només quan les dues variables d’entrada tenen valors diferents.
L’operador XOR en les expressions algebraiques és el símbol  , un signe de suma encerclat.
, un signe de suma encerclat.
En el cas de tenir més de dues entrades, podeu recordar com funciona una porta XOR si recordeu el següent:
La sortida d’una porta XOR és 1 només si hi ha un nombre senar d’entrades a 1.
La figura 14 mostra els símbols d’una porta XOR, la seva expressió algebraica i la seva taula de veritat.










