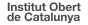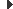Principis de les màquines rotatives de corrent altern
Les màquines elèctriques, quant a la seva utilització, tant poden transformar energia elèctrica en energia mecànica com els motors o a l’inrevés, transformen energia mecànica en energia elèctrica com els alternadors. Segueixen l’equació de la llei de Laplace, que ens quantifica la força que rep un conductor pel qual passa un corrent i és exposat a un camp magnètic:

a on:
- i = intensitat
- l = longitud del conductor
- β = densitat de flux magnètic
I l’equació de la llei de Faraday que quantifica la força electromotriu (f.e.m.) induïda en un conductor que es mou en un camp magnètic:

a on:
- v = velocitat
- l = longitud del conductor
- β = densitat de flux magnètic
Qualsevol màquina complirà aquest dos principis, i el principi de força serà més revelant en les màquines elèctriques com un motor, ja que les càrregues afectaran aquest principi per aconseguir l’estabilitat de la màquina, i quant al principi de força electromotriu induïda, serà més específica dels alternadors, no perquè els motors no la pateixin, sinó perquè l’estabilitat de la tensió de sortida és característica dels alternadors.
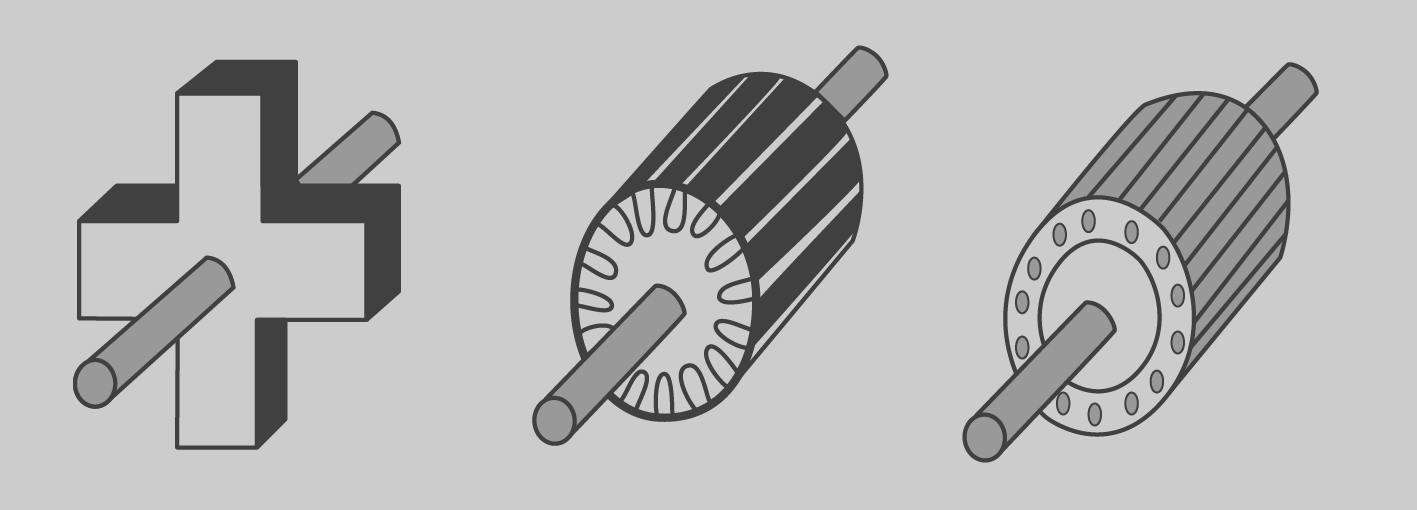
Principalment hi ha dues classes de màquines respecte el seu funcionament intern, les màquines síncrones en què el camp magnètic es genera a partir d’una font externa de potència de CC, i les màquines d’inducció o asíncrones, en què el camp magnètic és generat per inducció dels seus debanats. Els seus estators són iguals, però els rotors també són diferents: el rotor de pols sortints és de màquines síncrones, el de gàbia és de màquines asíncrones i els rotors bobinats són comuns, però els de màquina síncrona porten excitatriu.
Les màquines síncrones indiquen, tal com s’anomenen, que el camp elèctric respecte del camp magnètic giren a la vegada, o sigui, sincrònicament, i principalment s’utilitzen com a generadors d’altern anomenats alternadors.
Les màquines d’inducció o asíncrones generalment són utilitzades com a motors, en què hi ha un lliscament (s), i aquest lliscament és expressat en percentatge:

en què:
- nsinc = velocitat de sincronisme, en rpm
- n = velocitat nominal, en rpm
A més, podríem classificar les màquines elèctriques d’altern segons la seva potència, però si ens fixem en l’alimentació elèctrica que ens diu l’entorn on treballaran, parlem de màquines universals, monofàsiques i trifàsiques.
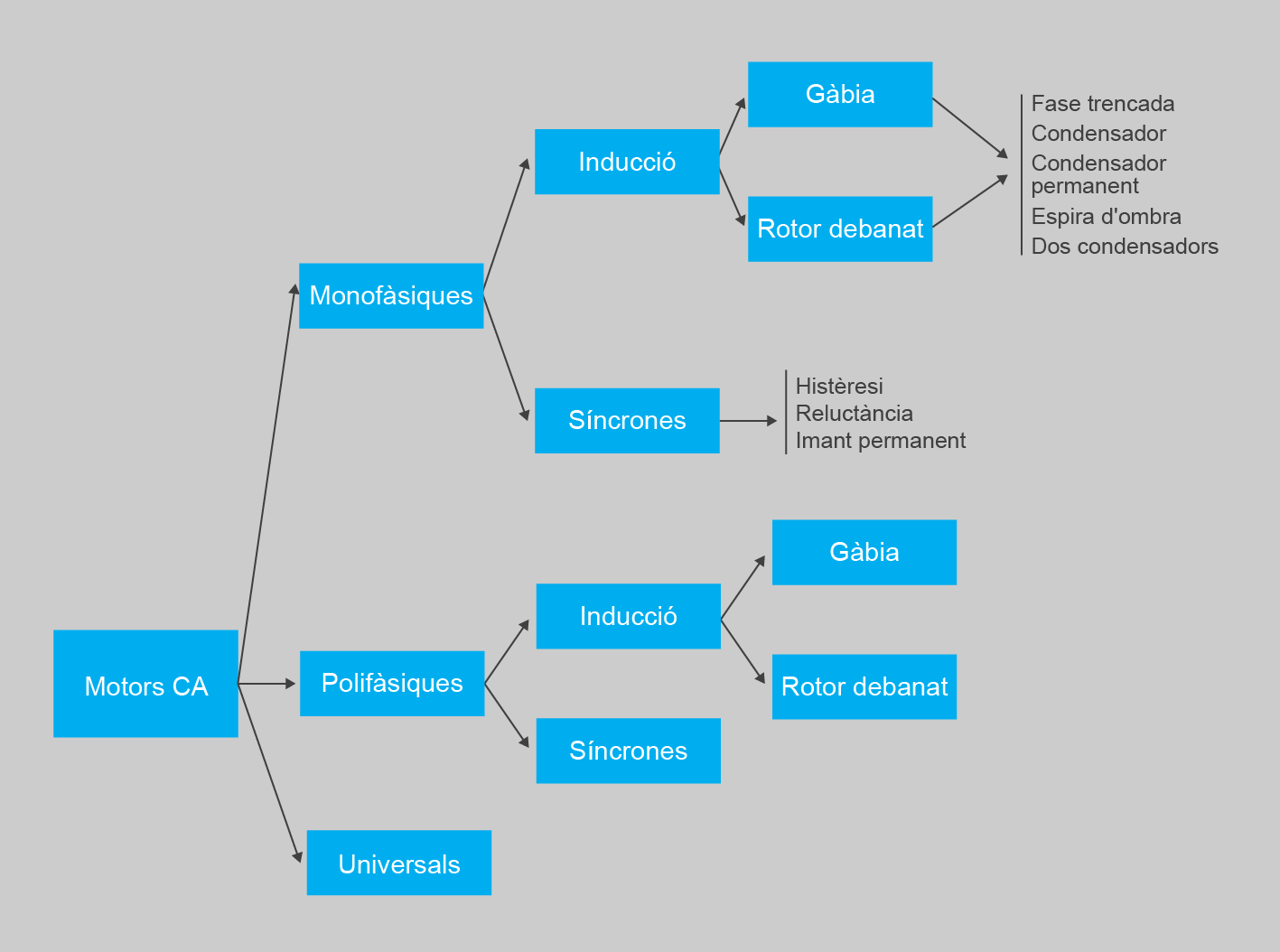
Les màquines monofàsiques s’utilitzen en un entorn més casolà i seran de menys potència que les trifàsiques, que són més utilitzades a la indústria. En la figura podeu veure una classificació de les màquines monofàsiques.
Característiques constructives de les màquines elèctriques rotatives de corrent altern
Les màquines rotatives d’altern bàsicament estan constituïdes pel següent:
- Carcassa, que serveix per aïllar-la elèctricament amb l’exterior; si aquesta és metàl·lica evita cops mecànics i forma part de la protecció elèctrica, i si a més porta aletes refrigera la màquina.
- Estator, que, com indica la paraula, és estàtic, no es mou i té les bobines de l’induït sobre un nucli d’aliatge fèrric o ferromagnètic format per una corona de xapes magnètiques aïllades entre si i amb ranures on estan allotjades els debanats (figura); els terminals dels debanats estan connectats en la placa de borns.
- El rotor, que gira sobre el seu eix i té les bobines de camp allotjades en les ranures del nucli ferromagnètic, format per un cilindre de xapes magnètiques aïllades entre si.
A més de les diferències del seu estator (monofàsiques, trifàsiques,…), i les diferències de com són els seus camps magnètics rotacionals (asíncrons i síncrons), tenen altres diferències específiques respecte a la seva constitució del rotor, si és bobinat (rotor debanat) o d’aliatge d’alumini (gàbia d’esquirol), de pols sortints, etc.
El rotor pot ser en gàbia d’esquirol (format per unes barres d’alumini, unides pels extrems a dos anells) o de rotor bobinat (format per un debanat, construït pel mateix nombre de pols que el de l’estator i connectat en estel a tres anells, connectats en curtcircuit amb un reòstat). El rotor de pols sortints (figura) s’utilitza en màquines síncrones, normalment quan són de dos o quatre pols, i també s’utilitza el rotor no sortint si té quatre o més pols.
Els tipus de rotors existents apareixen a la figura.
El rotor de gàbia (figura) està format per fines làmines ferromagnètiques encunyades i muntades en una estructura d’alumini, i amb dues tapes laterals d’alumini. És el més utilitzat als motors asíncrons, pel rendiment i el cost de fabricació.
Els motors de corrent altern se subdivideixen en tres tipologies:
- Motors universals
- Motors sincrònics
- Motors d’inducció o asíncrons
En la figura hi ha una classificació més específica dels motors de corrent altern.
La màquina com a generador i motor
En totes les màquines hi ha una sèrie de magnituds comunes, com són:
- El moviment o la rotació de la màquina.
- La força electromotriu induïda.
- El parell de forces.
- Les pèrdues.
- La placa característica.
Rotació de la màquina
En una màquina bipolar el recorregut mecànic o polar coincideix amb el recorregut geomètric o real (la volta real de la màquina són 360°).

El recorregut elèctric és el que fa el rotor per generar un cicle elèctric, i es genera un cicle elèctric cada vegada que es passa per un conjunt N-S o joc de pols (p); per tant, en una màquina bipolar coincideix amb el recorregut polar, que és el nombre de jocs de pols que ha recorregut la màquina. A cada volta real de la màquina és:
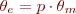
La freqüència elèctrica (fe) s’expressa en hertzs (Hz), que són cicles per segon. La freqüència mecànica (fm) s’expressa en revolucions per segon, que és exactament la mateixa cosa designada de manera diferent per diferenciar el concepte (però físicament és el mateix).
La velocitat mecànica es mesura en rpm = cicles per minut. Utilitzant el factor de conversió de temps podrem passar de Hz a rpm:

La velocitat mecànica també es pot mesurar en rad/s. Utilitzant el factor de conversió de temps podrem passar a rpm.
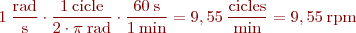
Què passa quan la màquina té més de dos pols?
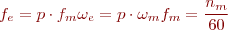
Passa que l’angle recorregut, la freqüència i la velocitat elèctrica queden igualats als paràmetres mecànics per la meitat del nombre de jocs de pols, i si expressem la freqüència mecànica fm en rps, podem dir que la relació entre la freqüència elèctrica fe i la velocitat de rotació del camp magnètic (n) és:
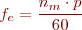
en què:
- nm = velocitat mecànica, en rpm
- p = parells de pols
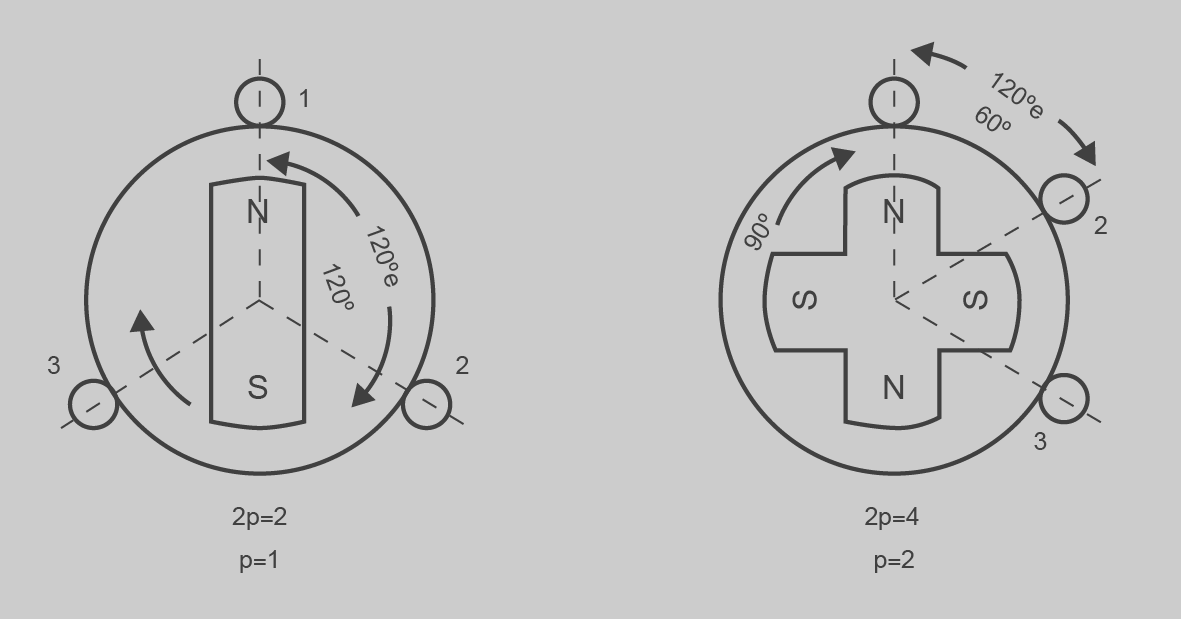
Cada volta real concebrà tants cicles elèctrics de fase com jocs de pols tingui la màquina. En cas d’una màquina trifàsica funciona igual, si suposem que cada p = tres jocs de parells de pols (un per a cada fase):
- Si p = 1 tindrem un recorregut polar de 120°
- Si p = 2 el recorregut serà de 60°
- … i així successivament

Amb velocitats relativament lentes de la màquina, agafant un gran nombre de pols a l’inductor es pot arribar a freqüències com 50 cicles/s amb n = 250 rpm, i calen 12 parells de pols en l’inductor.

Força electromotriu induïda
Quan parlem de força electromotriu induïda estem parlant d’alternadors. En els alternadors observem que el valor màxim de la f. e. m. induïda és:

Com que ω = 2·π·f, i en ser sinusoïdal l’ona, el valor eficaç és el màxim dividit per √2, es tindrà per al valor eficaç de la f. e. m. induïda l’expressió:
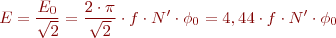
Si anomenem N el nombre de feixos actius, suposant que cada espira té dos feixos o conductors totals de la màquina (N = 2·N’), l’expressió es podrà escriure:

en què:
- Φ0 és el flux, en Wb
- E = f. e. m. induïda, en V
- Debanat concentrat amb un total de N conductors
En la pràctica, el debanat està distribuït sobre tota la perifèria de l’estator, cosa que fa que la suma de les f. e. m. de cada espira estigui desfasada, i per això la f. e. m. total haurà de ser la suma geomètrica i no aritmètica de les f. e. m. de cada espira. A més a més, el gruix d’una bobina no correspon al pas polar, o sigui, que si un conductor d’una espira està a sota i al centre d’un pol nord i l’altre conductor no està al centre del pol sud següent, es produeix un escurçament de la bobina.

en què:
- Kd = coeficient de distribució
- Ka = coeficient d’escurçament
Com que  , no tindrem en compte aquests coeficients al mateix temps, i llavors suposarem que és exacta l’expressió de la f.e.m. induïda en un alternador.
, no tindrem en compte aquests coeficients al mateix temps, i llavors suposarem que és exacta l’expressió de la f.e.m. induïda en un alternador.
Si en lloc de col·locar un joc N’ d’espires es col·loquen tres jocs d’espires desfasades en l’espai 120° elèctrics o magnètics, es tindrà un sistema trifàsic de tensions, i l’expressió anterior indicarà el valor de la tensió induïda per fase a la màquina si N és el nombre de conductors per fase.
Parell de forces
Les màquines elèctriques desenvolupen una força centrífuga, més característica als motors com a força d’arrossegament, o moment intern. Si es fa nominal (Mn), es dóna com a valor característic del motor. És una força a una distància, expressat en N·m:
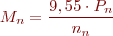
en què:
- Pn = potència nominal, en W
- nn = velocitat nominal, en rpm
A tota acció correspon una reacció. Davant el moment intern Mi, que és el moment de força que pot arrossegar la màquina, apareix el moment resistent Mr, que representa la càrrega que ha d’arrossegar el motor. Si Mi > Mr el motor girarà, i apareixerà una velocitat de gir n.
Pèrdues. Balanç de potències
Les pèrdues a les màquines elèctriques tenen les mateixes denominacions (CC o CA) i segueixen un ordre o l’altre, segons siguin generadors o motors. Les pèrdues són:
- Pèrdues del coure, del rotor i de l’estator, degudes a l’escalfament dels conductors.
- Pèrdues del nucli, degudes a la histèresi i als corrents parasitaris.
- Pèrdues mecàniques, degudes a la fricció dels rodaments i als efectes vendaval; si s’ajunten amb les del nucli s’anomenen pèrdues rotacionals de la màquina en buit.
- Pèrdues addicionals; per convenció els assignem 1% de la potència de sortida de la màquina.
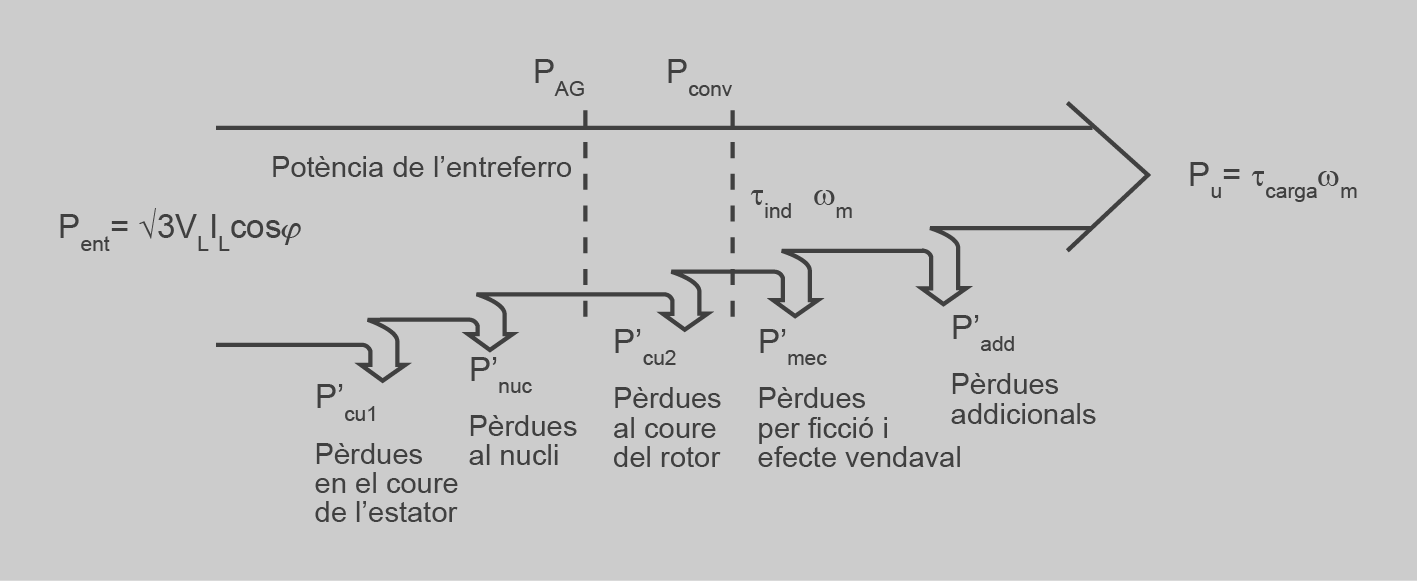
Les potències van disminuint, des de la lliurada fins a l’aprofitable, a mesura que es produeixen les pèrdues (figura). La relació que tenen entre elles s’anomena balanç de potències.
S’anomena balanç de potències la relació entre la potència subministrada o d’entrada, la potència aprofitable o útil i les pèrdues. Les potències van disminuint des de l’entrada fins a l’aprofitable, a mesura que es produeixen les pèrdues.
Bàsicament, les potències que intervenen són:
- La potència d’entrada (Pent o Pi), potència consumida (Pcon) o potència absorbida (Pabs); és la potència elèctrica d’alimentació de la màquina.
- Les pèrdues del coure, del rotor (P’cu1) i de l’estator (P’cu2), degudes a l’escalfament dels conductors, donaran pas a la potència convertida (Pconv) o potència mecànica (Pmec), menyspreant les pèrdues en el ferro produïdes en l’estator.



- Les pèrdues del nucli (P’nuc) són degudes a la histèresi i als corrents parasitaris, produïts al rotor.
- Les pèrdues mecàniques (P’mec), degudes a la fricció dels rodaments i als efectes vendaval; si s’ajunten amb les del nucli s’anomenen pèrdues rotacionals (P’rot).
- Pèrdues addicionals (P’add); per convenció els assignem un 1% de la potència de sortida de la màquina i donen pas a la potència útil (Pu).

El rendiment, expressat en percentatge, és:
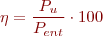
Exemple de balanç de potències
Un motor asíncron trifàsic indica en la seva placa de característiques 230 V/50 Hz, a plena càrrega i amb cos φ = 0,85, i té un rendiment del 83%. Si la seva potència útil és de 15,1 kW, la intensitat en buit és el 33,2% de la intensitat a plena càrrega, amb un cos φ = 0,2 en buit. Calculeu:
- La potència absorbida
- El corrent consumit a plena càrrega
- Les pèrdues rotacionals
- El rendiment en buit.
Solució
La potència absorbida és:
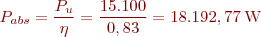
El corrent a plena càrrega:
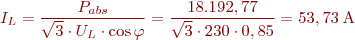
Les pèrdues rotacionals, menyspreant les pèrdues addicionals, són la diferència entre la potència útil i la potència convertida. Per tant, equival a la potència en buit:


$$P{buit}=\sqrt{3}\cdot U{L}\cdot I{buit}\cdot \cos\varphi{buit}=$$
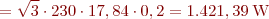
El rendiment en buit:
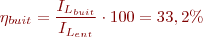
Placa de característiques
La placa de característiques d’una màquina elèctrica és la identificació de la màquina; té dos tipus de dades, anomenades nominals. A la figura en veiem un exemple desglossat, amb:
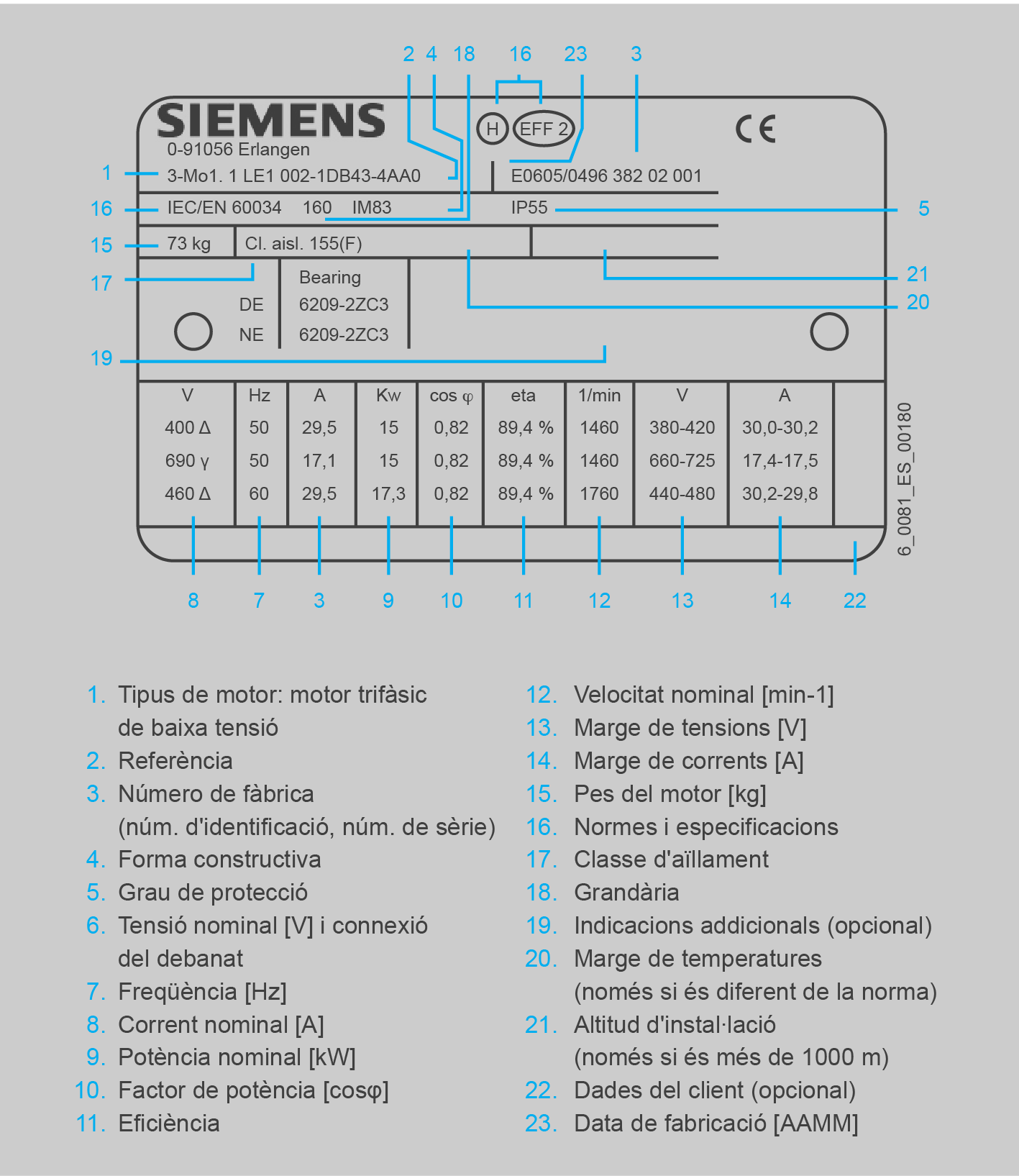
- Dades constructives, de control i d’identificació.
- Dades tècniques:
- Potència de plena càrrega (potència útil que és capaç de subministrar en règim de funcionament continu sense que l’escalfament sigui excessiu).
- Tensió per a la qual està construït.
- Freqüència de la xarxa d’alimentació.
- Intensitat que absorbeix a plena càrrega.
- Velocitat a plena càrrega en rpm.
- Factor de potència a plena càrrega.
El motor asíncron trifàsic tindrà dues tensions i dues intensitats nominals, perquè la connexió pot ser en estrella o triangle segons la tensió de la xarxa.
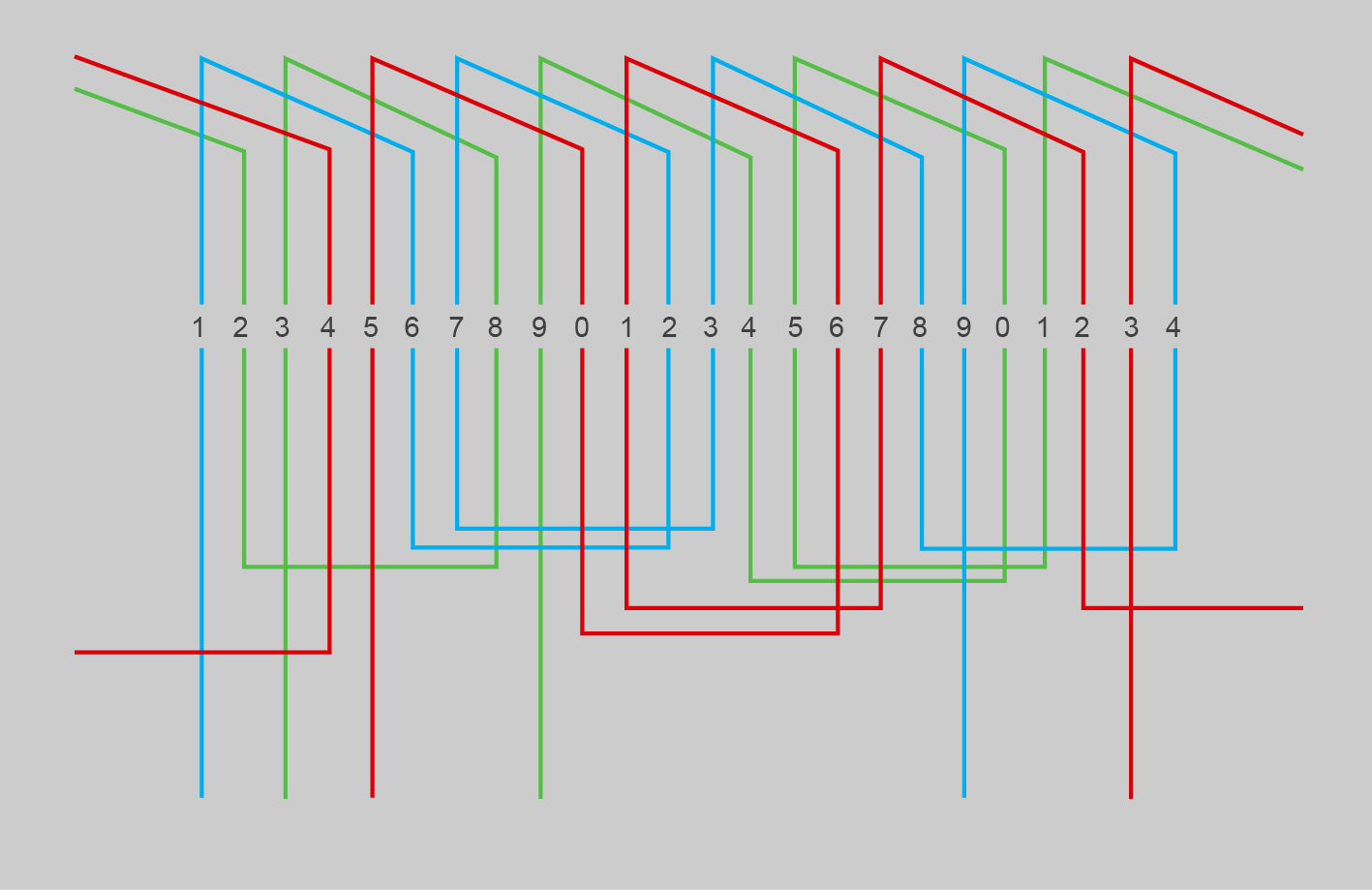
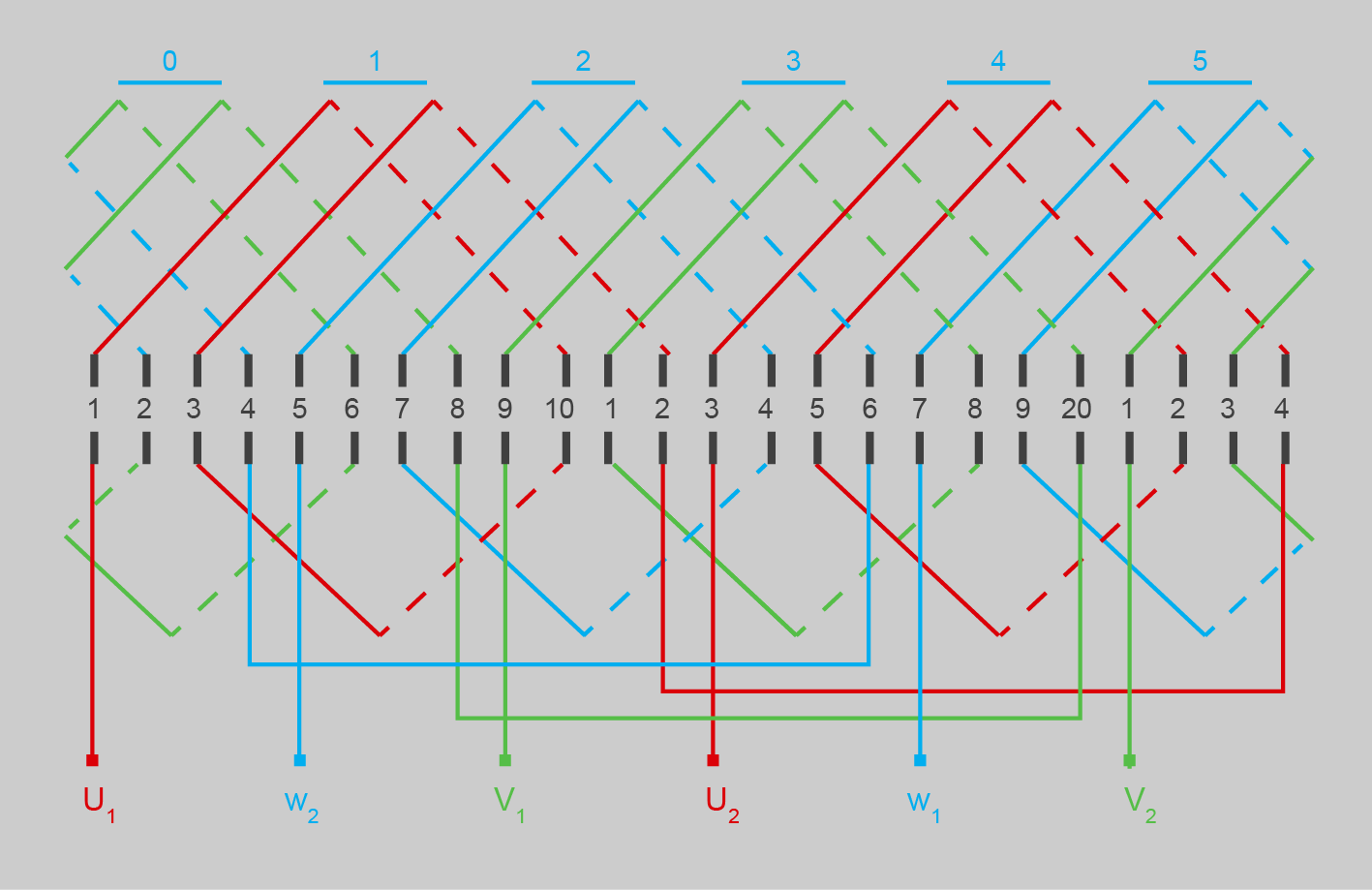
Els bobinatges estatòrics i rotòrics
Els bobinatges de les màquines de corrent altern tenen les mateixes denominacions que els de continu, amb les variacions pertinents als trifàsics de col·locació dels jocs de bobines a 120°.
Aquest bobinatges estan enrotllats als nuclis formant els circuits magnètics.
Els circuits magnètics. Rotor i estator
La missió del nucli ferromagnètic és que la inducció sigui màxima i les pèrdues mínimes, tenint en compte la corba de saturació del material ferromagnètic; aquesta va en consonància amb la potència nominal del motor, i si no sobrecarreguem el motor estarem treballant dins d’un marge en què el nucli no se saturarà. Els corrents parasitaris o de Foucault es minimitzen amb les làmines fines, separades per l’aïllament de vernís, que redueixen els corrents paràsits que hi circulen. El baix contingut de carboni fa del nucli un material magnètic suau amb pèrdues baixes per histèresi.
Els debanats estatòrics
En la pràctica cada fase del debanat estatòric està formada per diversos conductors formant bobines, connectades de manera que se sumen les forces electromotrius engendrades als conductors i es col·loquen en les ranures del seu nucli. El bobinatge de cada fase és de tipus tambor i obert (amb principi i final). Les fases han de ser idèntiques i desfasades entre si l’angle característic del sistema (120° elèctrics en el debanat trifàsic).
Les bobines del debanat estan reunides formant grups, que poden ser, segons la seva forma:
- Concèntrics: els costats actius d’una mateixa fase, situats sota els pols consecutius, units per caps concèntrics, segons la figura.
- Excèntrics: els costats actius d’una mateixa fase, situats sota pols consecutius, units per caps iguals, segons la figura.
Segons la forma de connexió dels grups de bobines d’una mateixa fase, el debanat pot ser connectat:
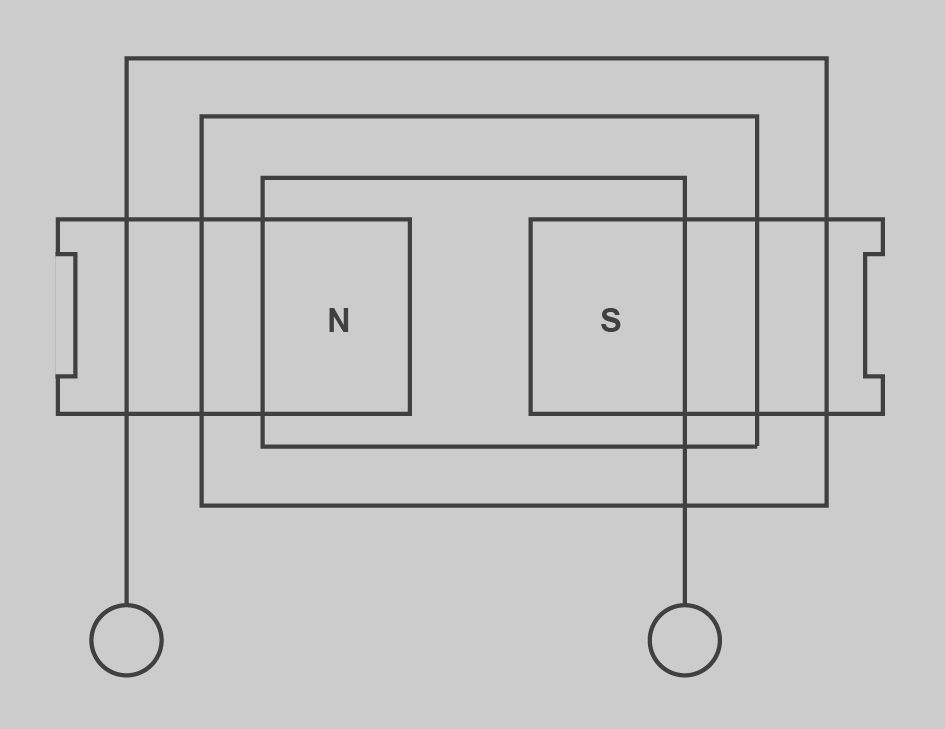
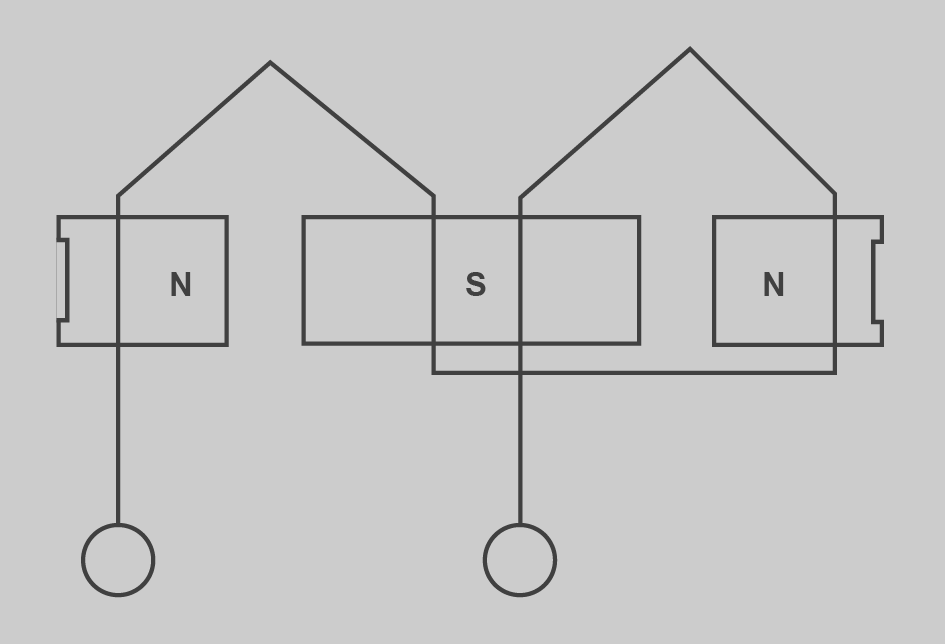
- Per pols (figura): el final d’un grup de bobines està connectat amb el final del següent i el principi d’un grup amb el primer del següent deixant sense connectar el principi del primer grup i el principi de l’últim, que seran el principi i el final, respectivament, de la fase. El nombre de grups per fase és igual que el nombre de pols (G = 2·p). El nombre total de grups és el nombre de grups pel nombre de fases (G = 2·p·q).
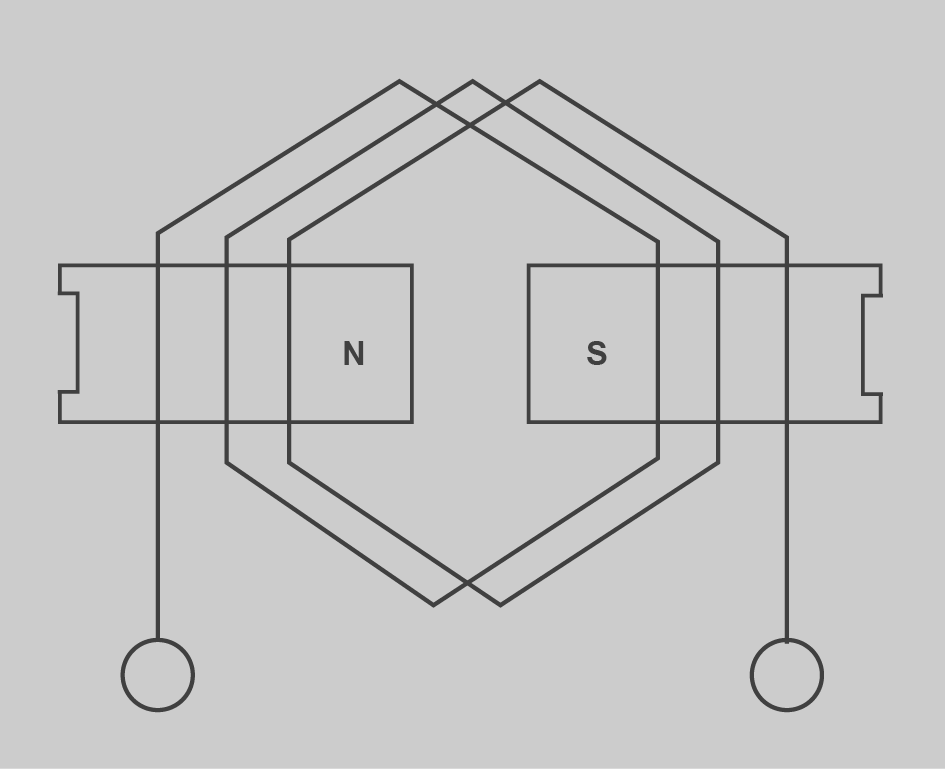
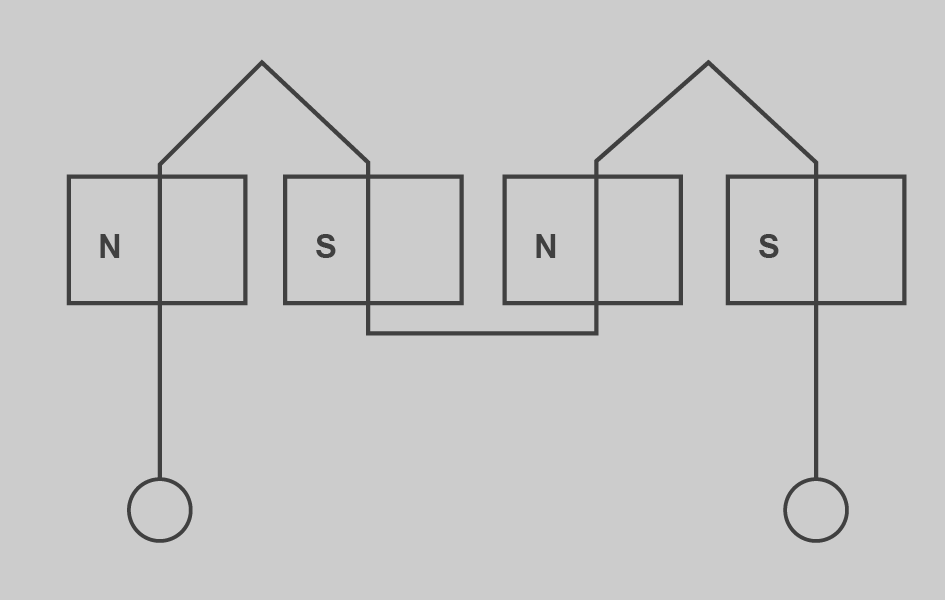
- Per pols conseqüents (figura): el final d’un grup de bobines està connectat amb el principi del següent deixant sense connectar el principi del primer grup i el final de l’últim, que seran el principi i el final, respectivament, de la fase. El nombre de grups per fases és igual que el nombre de parell de pols (G = P). El nombre total de grups és el nombre de grups per fase (G = P·q)
Bobinatges generals
Les ranures que ocupa el bobinatge per pol magnètic i per fase és, anomenant n el nombre de ranures:
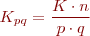
El nombre de bobines:
- Bobinatge d’una capa: el nombre de bobines B és la meitat de ranures B = K/2
- Bobinatge de dues capes: el nombre de bobines B és igual que el nombre de ranures: B = K
El nombre de bobines per grup u és el nombre de bobines total dividit pels grups totals de bobinatge:
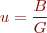
El pas dels principis de fase en un bobinatge trifàsic, amb un angle de desfàs de 120°, per a bobinatges trifàsics, és el nombre total de ranures entre principis de fase del bobinatge:
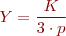
L’amplada de ranura o pas de ranura (Y) és l’espai mesurat en graus entre ranures adjacents. Excepte en màquines molt petites, el bobinatge serà de doble capa, amb menys ranures per bobina i connexions terminals més senzilles.
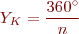
El pas de bobina o pas polar ( ) és l’angle entre els dos feixos actius de la bobina; si el mesurem en nombre de ranures Y per a cada pol de la màquina tindríem: Y = K/2·p.
) és l’angle entre els dos feixos actius de la bobina; si el mesurem en nombre de ranures Y per a cada pol de la màquina tindríem: Y = K/2·p.
Els pols magnètics naturals, sense tenir en compte el nombre de pols, estan posicionats en les màquines a 180° elèctrics, però quan es bobinen les màquines, com que s’ha de tenir en compte el nombre de pols, no és possible sempre fer-ho a 180°, i això dóna pas a noves denominacions; per exemple, en els generadors es poden bobinar igual que el pas polar (i s’anomena bobina de pas diametral), o a menys del pas polar (i són bobines de pas fraccionari o de pas encordat; per exemple, 5/6 de 180°, que són 150°).

El factor de pas de bobina, factor de pas polar, o també anomenat factor d’escurçament quan la bobina és de pas fraccionari, és:
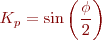
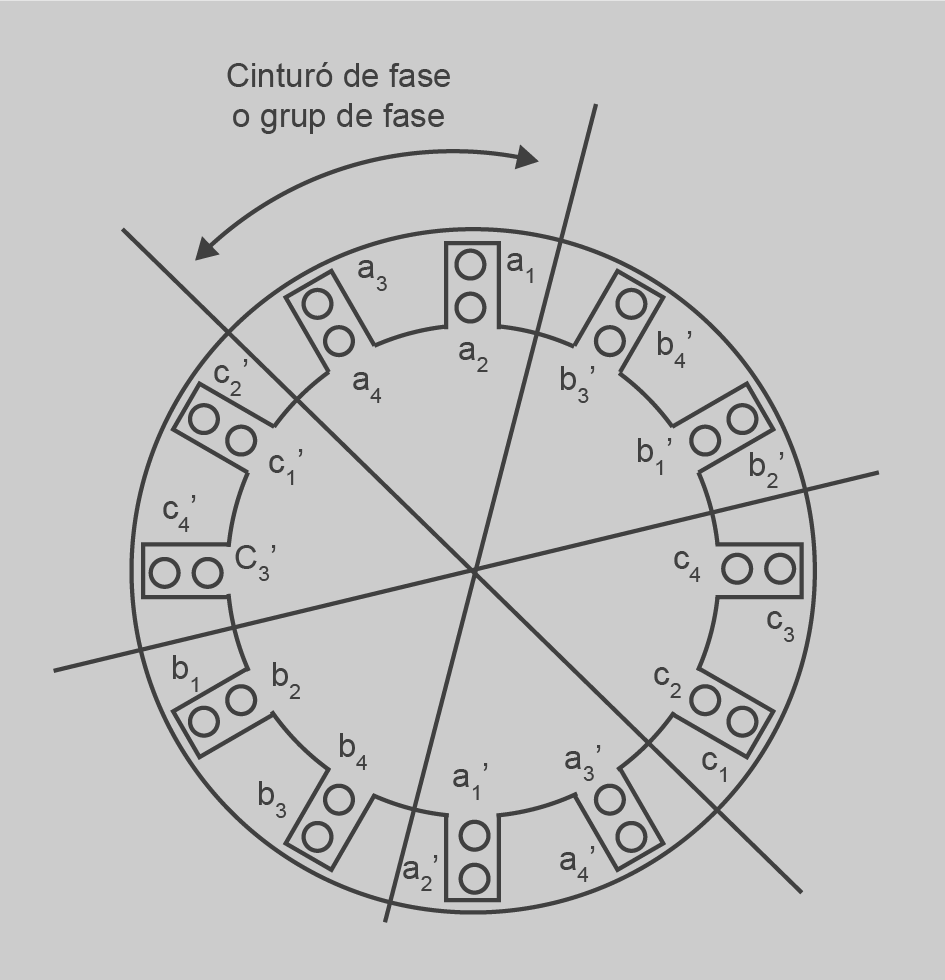
El cinturó de fase o grup de fase és l’espai de ranures on es col·loquen les bobines de cada fase. Hi ha 3·p cinturons de fase en un estator de p pols; en el pas fraccionari a la mateixa ranura poden coincidir bobines de dues fases quan el bobinatge és de doble capa. En la figura teniu representat un cinturó o grup de fase.
El factor d’amplitud o factor de distribució (Kd) és la reducció de tensió entre la bobina en ser distribuïda i la bobina concentrada.
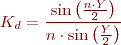
en què n és el nombre de ranures per fase.
El factor de pas i el factor de distribució es combinen en el factor de bobinatge Kpd i la tensió per fase en l’estator queda:

Bobinatges concèntrics
Aquests bobinatges se solen fer d’una capa i connectats per pols conseqüents (figura).
L’amplitud m del grup és el nombre de ranures que es troben en l’interior del grup de bobines: m = (q − 1) · K.
Si el nombre de bobines per grup u no fos un nombre enter n + 1/2, es col·loquen alternativament grups de n bobines i de n + 1 bobines.
Bobinatges excèntrics intercanviats sencers
Aquests bobinatges (figura) se solen fer d’una o dues capes i es caracteritzen per tenir un nombre de ranures per pol i fase enter K = nombre enter.
L’amplada de bobina o pas de ranura Yk pot ser menor o igual que el pas polar Yp. En el bobinatge d’una capa el pas de ranura ha de ser senar.
Bobinatges excèntrics imbricats fraccionaris
Aquests bobinatges s’executen en dues capes i connectats per pols. Es caracteritzen per tenir el nombre de ranures per pol i fase com un nombre fraccionari de la forma u = A/B, i la fracció és irreductible i B múltiple de 3.
Per saber la distribució en el bobinatge dels grups de ranures es fa una taula de distribució:
- En tres columnes es tracen B files de A punts.
- Es traça un senyal en el primer punt de la primera fila i en tots el que disten d’aquestes B unitats.
- Els senyals de la primera fila indiquen el nombre de ranures que corresponen a cada fase en primer pol.
- Els senyals de la segona fila indiquen el nombre de ranures que corresponen a cada fase en segon pol, etc.
L’amplada de bobina o pas de ranura Yk pot ser menor o igual que el pas polar Yp .
Exemple de bobinatge excèntric per pols
Farem un bobinatge d’un motor trifàsic bipolar excèntric de K = 24 ranures, 2p = 2 parells de pols, q = 3 fases, amb bobinatge d’una capa per pols.
Les característiques per fer el muntatge del motor són les mostrades a la taula.
| Estator de tipus xapa | IEC 80/6-8.80 | Ranures | 24 |
| Diàmetre exterior | 120 mm | Longitud | 75 mm |
| Diàmetre interior | 80 mm | Esquema | Bipolar |
| Tipus de bobinatge | Trifàsic excèntric bipolar per pols conseqüents | ||
| Grups | 6 | Bobines/grup | 2 |
| Pas de bobina | de 1 a 10 | Espires/bobina | 120 |
| Pes del coure | 110 g | Resistència fases | 21 Ω |
Descripció del muntatge
Ordre en el procés de bobinatge de les màquines de corrent altern:
- Càlculs del bobinatge i esquema
- Confecció de les bobines
- Aïllament de les ranures estatòriques
- Confecció de les bobines
- Col·locació de les bobines en les ranures
- Connexió de les bobines entre si
- Lligament del bobinatge
- Verificació elèctrica de l’enrotllament
| Tipus de bobinatge | Excèntric, per pols | Ranures | K = 24 |
| Nombre de ranures per pol i fase | 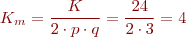 | Bobines | 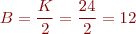 |
| Pols | 2·p = 2 | Fases | q = 3 |
| Grups del bobinatge | G = 2·p·q = 2·3 = 6 | Bobines per grup | U = B/G = 12/6 = 2 |
| Grups | 6 | Pas polar | 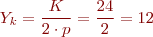 |
| Principi de fase | 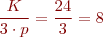 | Passos de bobina | YB = 1 a 13, s’escurça 3 unitats |
| Principis de fase | U-1, V-9, W-17 | ||
Càlculs del bobinatge i esquema
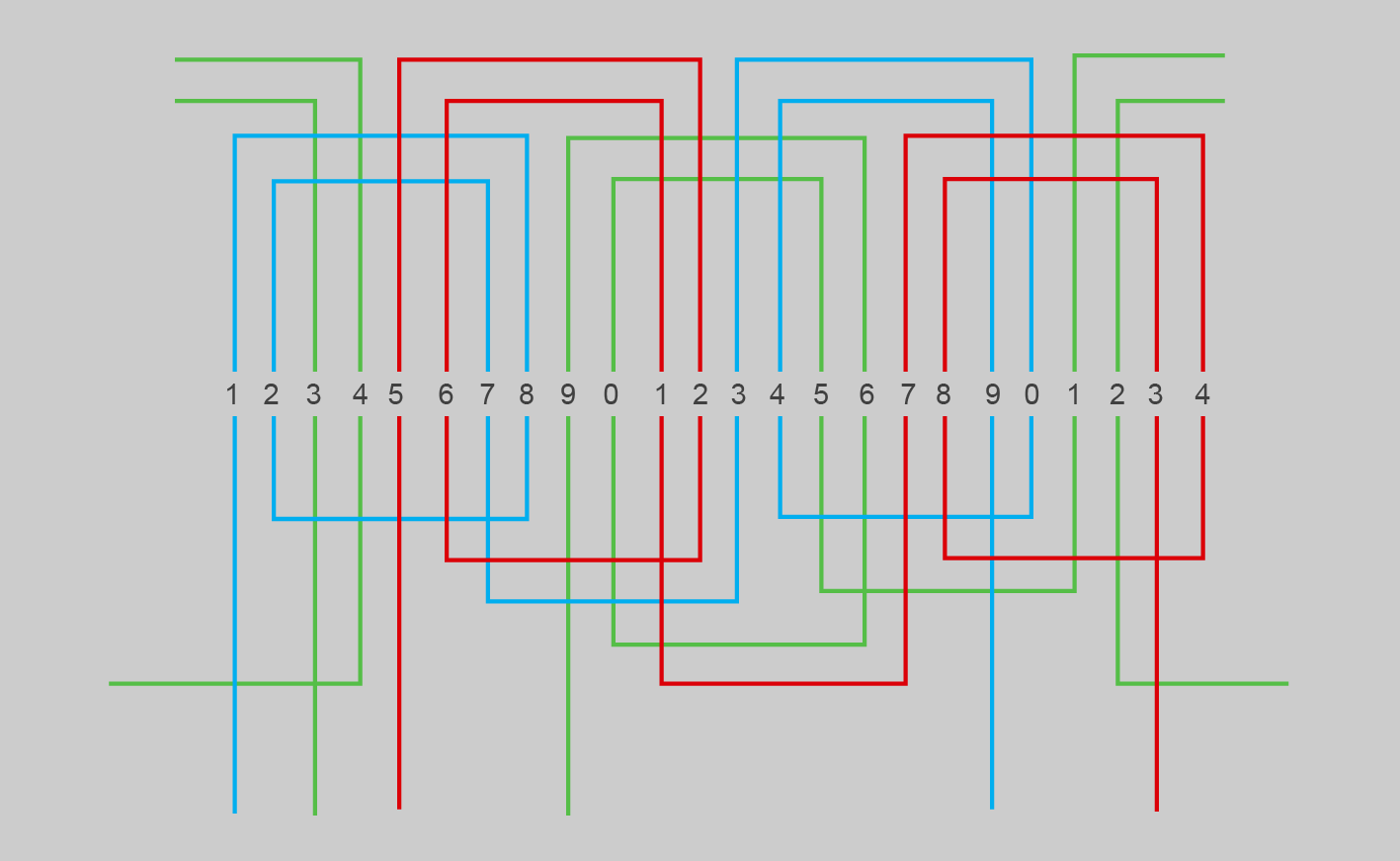
Els càlculs del bobinatge per muntar estan a la taula, i l’esquema del bobinatge excèntric es mostra a la figura següent:
Aïllament de les ranures estatòriques
L’aïllament es faria amb 24 cartons aïllants, tallats de manera que sobresurtin pels extrems de les ranures, el suficient perquè els conductors no arribin a tocar el nucli en cap moment, per evitar contactes en massa.
Confecció de les bobines
Amb un fil de coure es faria una espira i es deixarien lliures la resta de les ranures.
Motlle de la bobina
Es fa el motlle de la bobina; la mesura del motlle és de 12,5 cm.
Es col·loca el fil de coure sobre el motlle del conjunt de motlles excèntrics, es pren la distància que hi ha entre motlle i motlle, i per fer la resta de bobines es posa el comptador a 0 i es comença a bobinar; el nombre d’espires de cada bobina depèn del tipus de ranura del motor (en aquest cas és de 120 espires amb fil de 0,5 mm de diàmetre). Una vegada introduït el grup de bobines s’observa que no sigui ni gran ni petit, i si ho fos es modificarà. Cada bobina té un pes de 200g.
Col·locació de les bobines en les ranures
Les bobines han d’entrar en les ranures suaument; no les creuarem, ni les posarem a l’inrevés, perquè frenarien elèctricament el motor. S’alinearan les bobines consecutivament; en ser un bobinatge excèntric, el bobinatge quedarà trenat. Abans d’acabar el bobinatge aixecarem la 1, 3, 5, 7 perquè el trenat sigui perfecte. Finalment es posaran les cunyes de plàstic per aïllar les ranures de les bobines.
Connexions dels debanats
Connectarem el bobinatge comprovant que cada principi i final de grup surten de la ranura corresponent, segons l’esquema. Cadascun dels fils de l’empalmament portarà el tub aïllant de silicona. Es pelen els extrems del fil, sense deixar vernís, s’empalma en prolongació i s’estanya. Es desplaça el tub de silicona sobre l’empalmament fins que quedi cobert.
Tant el principi com el final de cada fase arriben a la placa de borns amb conductor flexible; aquests empalmaments també estaran lligats al cap del bobinatge. La vista de l’estator amb algun grup de bobines s’aprecia a la figura següent:

També s’hi poden apreciar els cartons i cunyes aïllants.
Lligament del bobinatge
El lligament del bobinatge es fa amb lliç engreixat, i aprofitant un tros de fil per confeccionar un tipus d’agulla. Les distàncies de les voltes amb el lliç seran uniformes, iguals que la subjecció. Utilitzarem el presspan, que és un cartró per separar els grups de bobines. Una vegada finalitzat el lligam amb un martell de goma o plàstic, es col·locarà el bobinatge al seu lloc, de manera que no toqui el rotor en el seu gir o l’induït.
Verificació elèctrica de l’enrotllament
Durant el procés de connexió, s’anirà comprovant la continuïtat del circuit. Una vegada acabades de connectar les bobines, se sotmetrà als assajos d’aïllament, formació de pols, derivacions a massa, etc.
Per comprovar la continuïtat del bobinatge s’utilitza un multímetre, posant les puntes en els extrems. Una altra comprovació és la derivació a massa, que consisteix que els principis de fase i la carcassa no donin continuïtat amb el mesurador.
Tanquem el motor amb els cargols i connectem les fases a una font d’alimentació, posem un amperímetre en sèrie amb el bobinatge i el mesurador per comprovar la tensió entre dos terminals. Els increments els farem de 20 en 20 volts i mesurarem els corrents i les rpm amb un tacòmetre, així fins a 230 V. A la taula hi ha els resultats en estrella i triangle de consum, i la velocitat a cada graó de 20 V.
| V (V) | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estrella | I (A) | 0,24 | 0,49 | 0,33 | 0,23 | 0,19 | 0,17 | 0,15 | 0,16 | 0,16 | 0,17 | 0,2 |
| rpm | 55,6 | 424,4 | 2.430 | 2.786 | 2.882 | 2.982 | 2.944 | 2.958 | 2.966 | 2.972 | 2.978 | |
| Triangle | I (A) | 0,8 | 0,4 | 0,3 | 0,29 | 0,28 | 0,31 | 0,35 | 0,39 | 0,44 | 0,5 | 0,6 |
| rpm | 355,6 | 2.725 | 2.895 | 2.946 | 2.966 | 2.976 | 2.983 | 2.986 | 2.989 | 2.990 | 2.991 |
Bobinatges trifàsics de pols commutables
Aquests bobinatges es connecten per pols conseqüents per la major polaritat i del punt mitjà de cada fase es treu una connexió per a la commutació del nombre de pols.
El pas de bobina, d’1 a 15 per a la doble capa, ens adverteix de la connexió de 6 ranures per les quals passarà la mateixa intensitat de fase.
A la figura apareix un esquema trifàsic de bobinatge amb pols commutables.
Bobinatges del motor asíncron monofàsic
Aquests bobinatges se solen fer concèntrics i d’una capa:
- El bobinatge principal ocupa dos terços de les ranures i el grup de bobines té l’amplitud d’un terç del pas polar.
- El bobinatge auxiliar o d’arrencament ocupa l’altre terç de les ranures i el grup de bobines els dos terços restants fins a arribar al pas polar.
El desfasament entre els principis de fase dels dos bobinatges (90° elèctrics) és, en ranures:
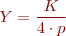
El debanat rotòric. Harmònics pel pas de bobina
Els harmònics són el resultat d’una sèrie de variacions adequadament acomodades en un rang o freqüència d’emissió electromagnètica i que afecten l’ona de tensió generada en una màquina o un altre sistema elèctric; aquesta freqüència dels harmònics és una freqüència múltiple de la freqüència fonamental.
Així, en sistemes amb freqüència de 50 Hz els n harmònics corresponen a n·f, el 2n., 3r., 4t. harmònics correspondrien a 100 Hz, 150 Hz i 200 Hz, i així successivament.
Els pas de bobina diametral genera harmònics de cinturó, i el pas de ranura genera harmònics de dent o de ranura, que ocasionen problemes, com són:
- Inducció d’harmònics en la tensió de sortida de la màquina.
- Interacció entre els harmònics de l’estator i el rotor que produeix moments de torsió, que en les màquines d’inducció poden afectar la corba parell de torsió - velocitat del motor.
- Introducció de vibracions i sorolls.
- Augment de les pèrdues de nucli en introduir components de tensió a alta freqüència i corrents en les dents de l’estator.
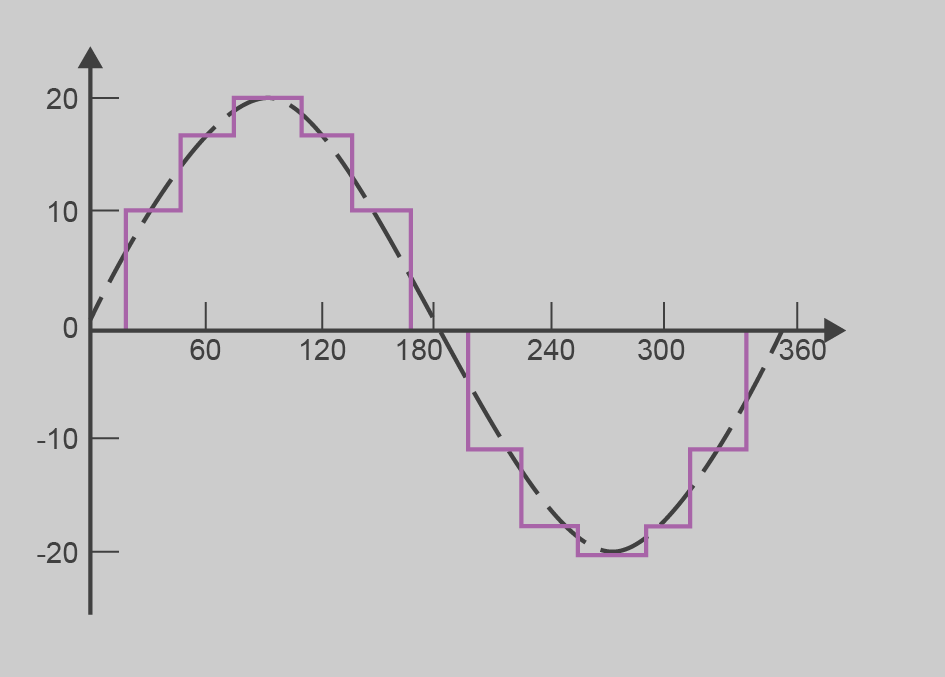
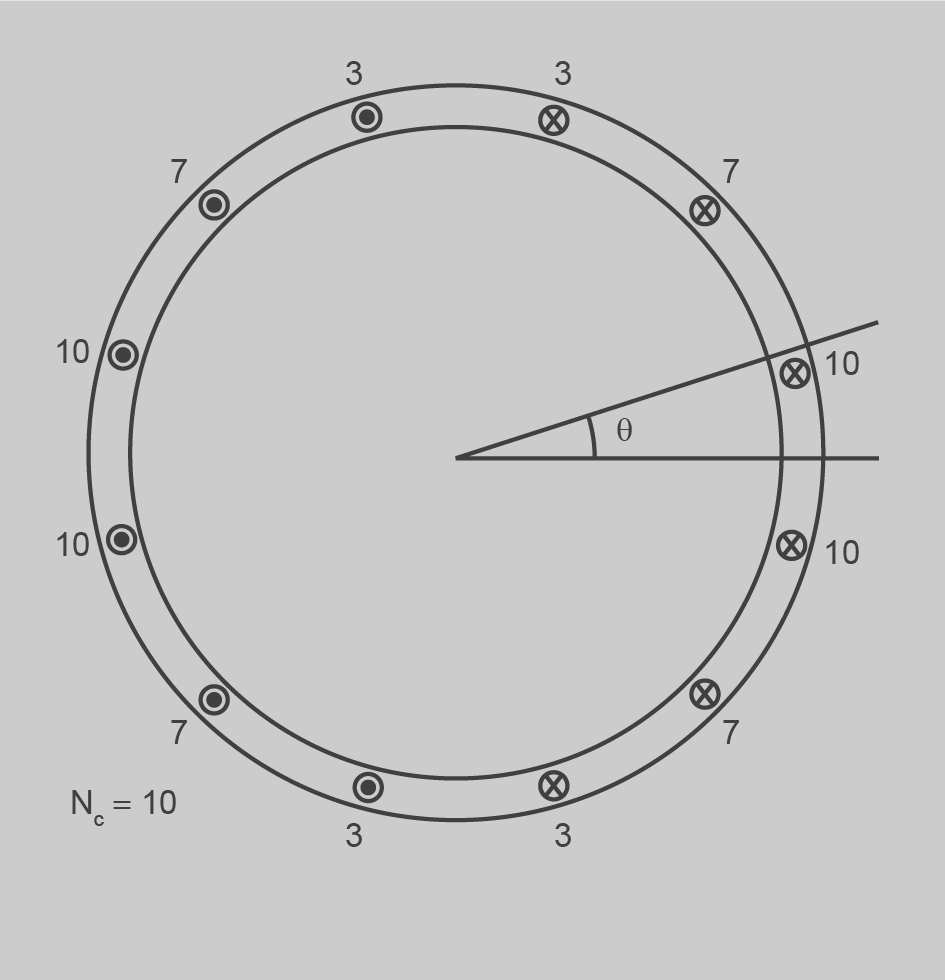
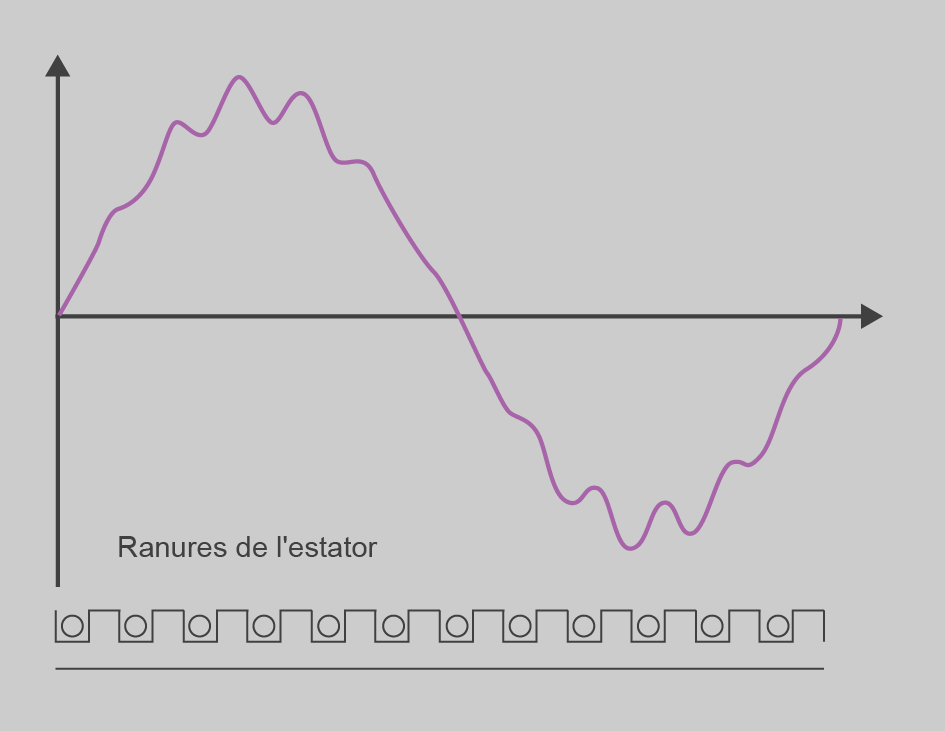
En la figura es pot apreciar la comparació de la distribució de la força magnetomotriu (f.m.m.) resultant amb la distribució ideal, de l’estator distribuït de la figura.
La tensió és simètrica cap al centre del flux del rotor, de manera que no hi ha harmònics parells en la tensió de fase. Els tercers harmònics són idèntics en les màquines trifàsiques: aquest harmònics es contraresten en estrella, i en triangle queden aplicats a les impedàncies internes de la màquina i no afecten tampoc la tensió de sortida. Són anomenats tercers perquè als seus múltiples també els passa (sisè, novè…). Les freqüències harmòniques restants perilloses són la cinquena i la setena, anomenades també harmònics de cinturó, i les freqüències harmòniques més altes (onzena cap amunt) es menyspreen, perquè pràcticament ja no afecten la tensió de sortida.
El factor del pas de bobina a la freqüència harmònica és:

en què n es refereix a l’harmònic n.
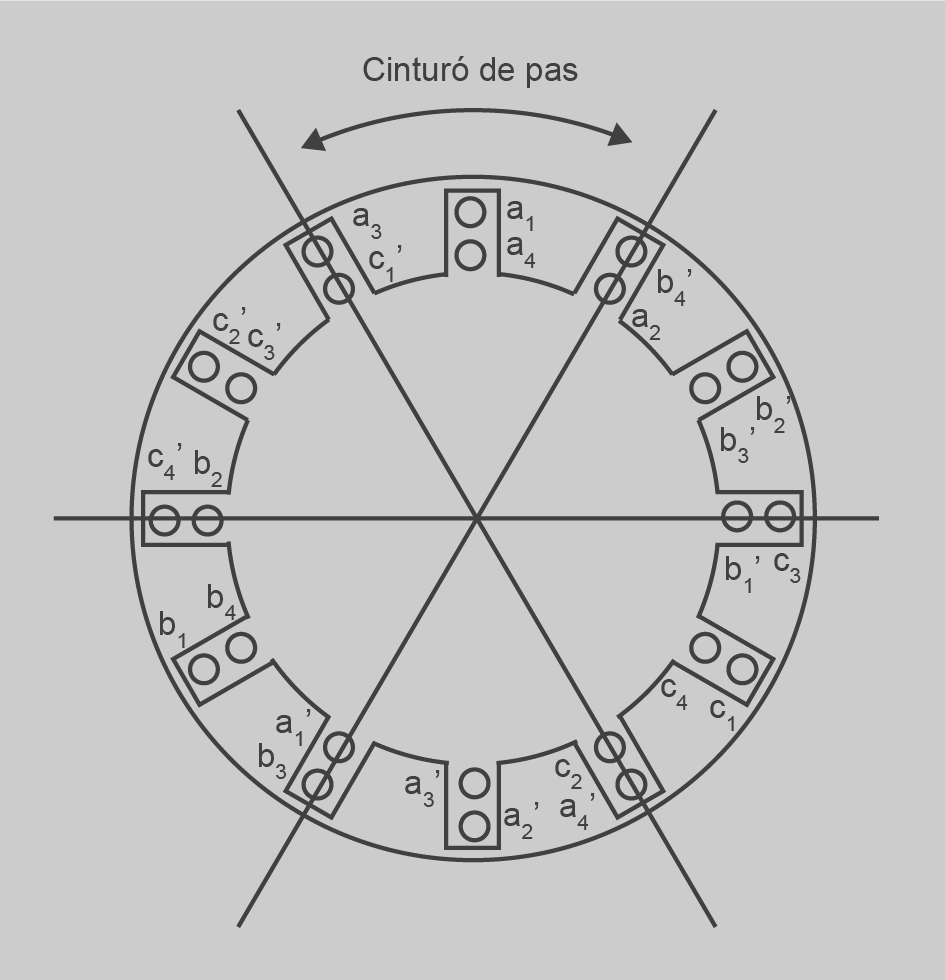
El pas fraccionari en l’estator evita severament la deformació en la tensió de sortida del generador deguda als harmònics que apareixen en la distribució sinusoïdal de la densitat de flux, i produeix una petita disminució en la tensió de sortida. El bobinatge de pas fraccionari millora la qualitat de la forma d’ona. A la figura tenim el cinturó de pas en un bobinatge de pas diametral amb doble capa.
Els espais que hi ha entre les ranures formen variacions regulars de reluctància que originen harmònics en la tensió de sortida; en la figura apreciem els harmònics de ranura generats en la densitat de flux de l’entreferro d’aire.
Aquests harmònics de dent o ranura són els número n en funció del nombre de pols (P) i ranures de l’estator (S):
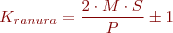
A on:
- M = enter que amb valor 1 produeix els harmònics de menor freqüència.
- S = nombre de ranures de l’estator
- P = parells de pols
Si M = 1, obtenim les freqüències menors: els harmònics de dent o ranura de menor freqüència són els que faran més nosa.
D’una altra banda, els bobinatges de ranura fraccionària en el rotor per pol, per exemple amb 2,5 ranures per pol, redueixen els harmònics de cinturó i de ranura.
Un altre procediment més comú, fonamentalment en els motors d’inducció, és que els conductors del rotor tenen una lleugera inclinació, de manera que quan mig conductor del rotor està sota una ranura de l’estator l’altra meitat està sota la ranura adjacent. Correspon a una distància d’un cicle elèctric complet de la menor freqüència harmònica de la ranura, i fa que les variacions de flux per harmònics en la ranura es cancel·lin entre elles.