Amplificadors operacionals
-
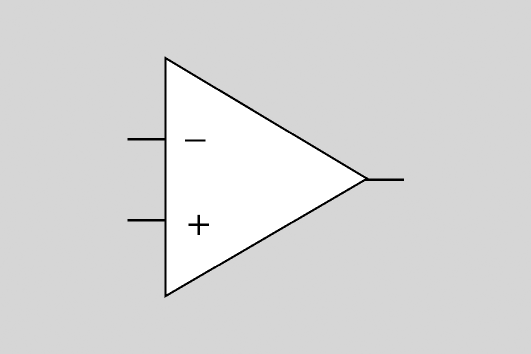
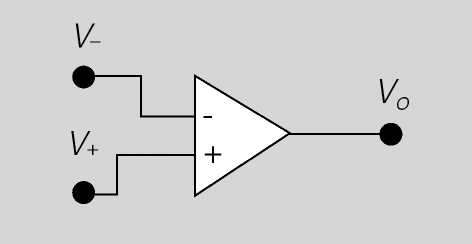
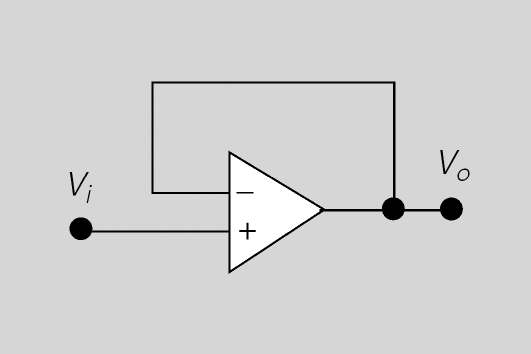
- Símbol de l'AO
L’amplificador operacional (AO) és un circuit integrat analògic. La seva característica principal és proporcionar un guany diferencial de tensió molt elevat. És un element utilitzat en múltiples aplicacions.
L’AO té dues entrades i una sortida (Vo). L’entrada inversora es representa amb el signe menys (V−) i l’entrada no inversora es representa amb el signe més (V+).
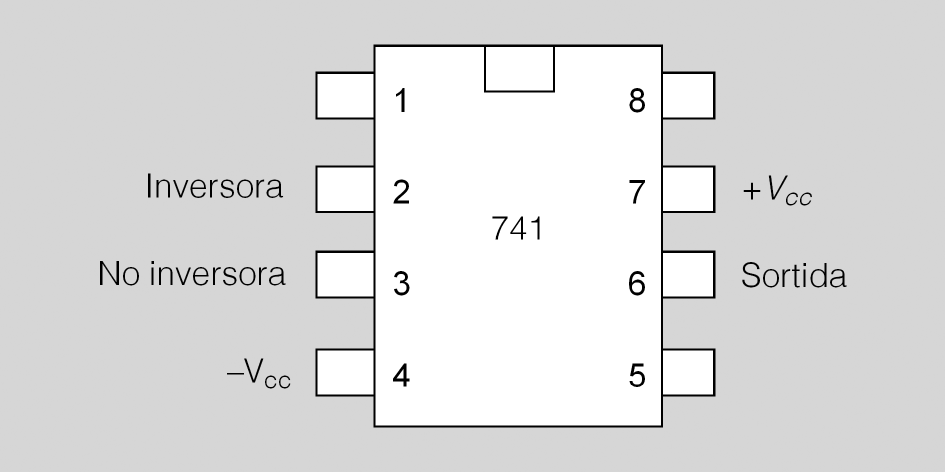
En el mercat hi ha gran quantitat i varietat d’AO i d’encapsulacions.
En la figura podeu veure el circuit integrat 741, amb la identificació dels seus terminals. Aquest xip conté en el seu interior un únic AO.
Característiques de l'amplificador operacional
Les característiques ideals de l’amplificador operacional són les següents:
- Guany de tensió en bucle obert: infinita.
- Resistència d’entrada: infinita.
- Resistència de sortida: 0.
- Ample de banda: infinit.
- Intensitats a les entrades V− i V+: 0.
Direm que l’AO està en bucle obert quan no hi hagi cap tipus de connexió entre la seva sortida i alguna de les seves entrades. En general, quan l’AO funciona en bucle tancat, la tensió a l’entrada inversora és igual a la tensió de l’entrada no inversora. D’això se’n diu curtcircuit virtual.
En general es considera que els amplificadors operacionals idealment treballen en curtcircuit virtual, que vol dir que es considera el següent:
- V+ = V−
- El terminals d’entrada V+ i V− no drenen corrent elèctric.
Depenent de les connexions externes que es realitzin a AO i els components utilitzats per realitzar-les, el circuit farà una funció o una altra.
L'amplificador operacional com a comparador
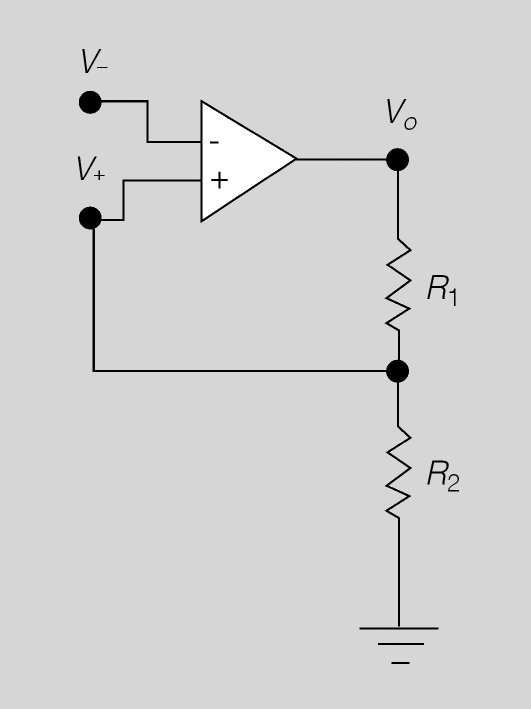
El circuit de la figura realitza la comparació de dues tensions: V− (entrada inversora) i V+ (entrada no inversora).
Comparador: V+ > V− → Vo = +VCC V− > V+ → Vo = -VCC
Si V+ és més gran que V−, la sortida és igual a la tensió positiva +VCC de l’alimentació.
Si V− és més gran que V+, la sortida és igual a la tensió negativa −VCC de l’alimentació.
Exemple de comparador
Teniu un AO comparador alimentat a +15 V i −15 V (és a dir, amb FA simètrica). Trobeu el valor de Vo si V+ = 2 V i V− = 1,5 V.
Solució:
Com que V+ > V−, la sortida Vo = 15 V.
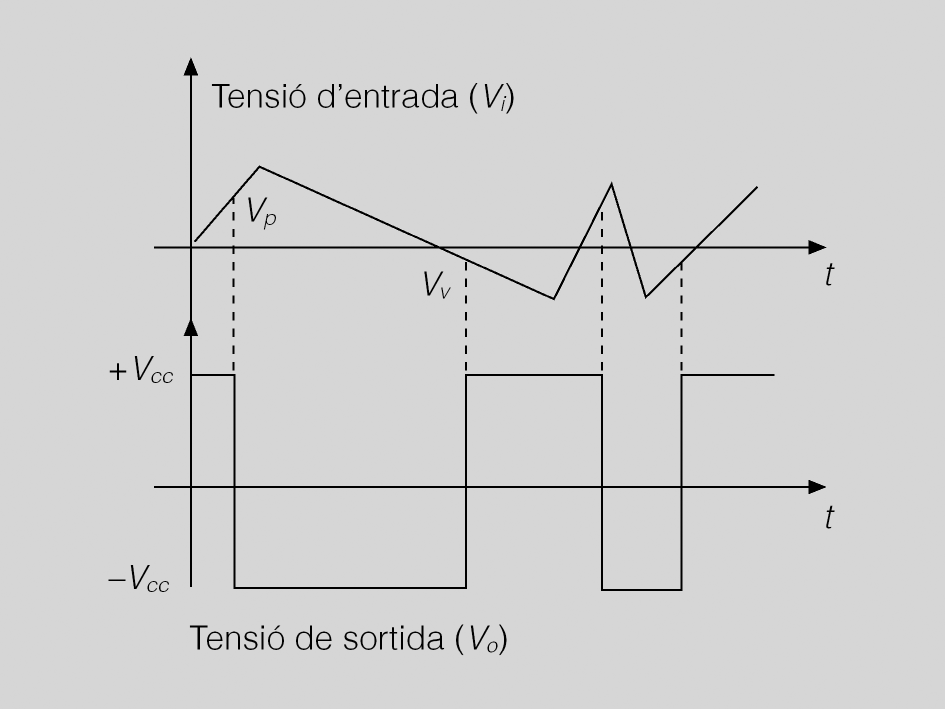
El comparador de la figura és de bucle obert, i té l’inconvenient que és molt sensible a les interferències, i això fa que la Vo commuti fàcilment de forma no desitjada. Per solucionar aquest problema es realitza el comparador de la figura. En aquest muntatge, el senyal que s’ha de comparar entra pel terminal inversor.
Les dues tensions de referència per les quals la sortida commuta són:


A on Vp és la tensió de pic i Vv és la tensió de vall (o tensió de pic negativa).
Si observeu la figura, el senyal Vo no varia fins que la Vi no hagi sobrepassat el valor de Vp. Un cop sobrepassat, Vo és igual a −VCC, i manté el seu valor fins que la Vi no tingui un valor més petit que Vv. En aquest moment Vo commuta a +VCC i és manté fins que Vi no sobrepassa Vp, i es repeteix el cicle.
Aquest sistema permet evitar rebots a la sortida del comparador en cas que la tensió d’entrada presenti algun petit arrissament.
L'amplificador operacional com a amplificador. Sumadors i restadors
Per definició, amplificar és multiplicar el senyal d’entrada d’un circuit per un número. D’aquesta manera, el que fan els amplifiacadors és multiplicar l’entrada per un número. Però els AO, en tenir dues entrades (positiva i negativa), permeten un ventall de configuracions d’amplificació associada a suma de senyals, resta de senyals i d’altres.
En definitiva, gràcies a les configuracions d’amplificació habituals dels AO parlarem de:
- Seguiment de tensió: quan l’amplificació valgui 1, és a dir, que la sortida és exactament igual que l’entrada (es fa servir quan un senyal de molt poca potència s’ha d’injectar a un circuit que només de connecta-lo faria malbé el senyal, amb un seguidor de tensió tenim un senyal de la mateixa forma però amb més potència).
- Amplificació inversora: quan el guany (el número pel qual es multiplica el senyal d’entrada) és negatiu, s’anomena inversió perquè es dóna la volta al senyal en canviar-la de signe.
- Amplificació no inversora: quan el guany és positiu.
- Amplificació amb suma: quan apart d’amplificar-los si cal, el sistema suma o resta senyals.
- Amplificació diferencial: quan el sistema amplifica la diferència entre el senyal d’entrada positiu i el negatiu (és una configuració molt habitual a sistemes a on el soroll o les interferències són crítics).
Seguidor de tensió
En la figura, podeu veure el seguidor de tensió. Aquest circuit s’utilitza per exemple com a adaptador d’impedàncies. La tensió de sortida és igual a la tensió aplicada a l’entrada.
Seguidor de tensió: Vo = Vi
Comprovació del funcionament del seguidor
Al circuit de la figura, queda patent que V+ = Vi i que V− = Vo.
Degut al curtcircuit virtual, sabem que V+ = V−. Així, igualant les anteriors equacions, obtenim: Vo = Vi
Amplificador inversor
El guany del circuit de la figura és determinat per les dues resistències, el signe negatiu indica que Vo està invertida respecte a Vi. Observeu la simulació de la figura: quan la Vi és negativa Vo és positiva i quan Vi és positiva, Vo és negativa.
A l’amplificador inversor el guany és:

Exemple d'amplificador inversor
Si R2 = 10 KΩ i R1 = 1 KΩ quin serà el guany del circuit? Si Vi = 1 mV, quin valor tindrà la sortida?
Solució:
Aplicant la fórmula del guany:
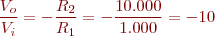
La tensió de sortida serà:
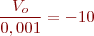

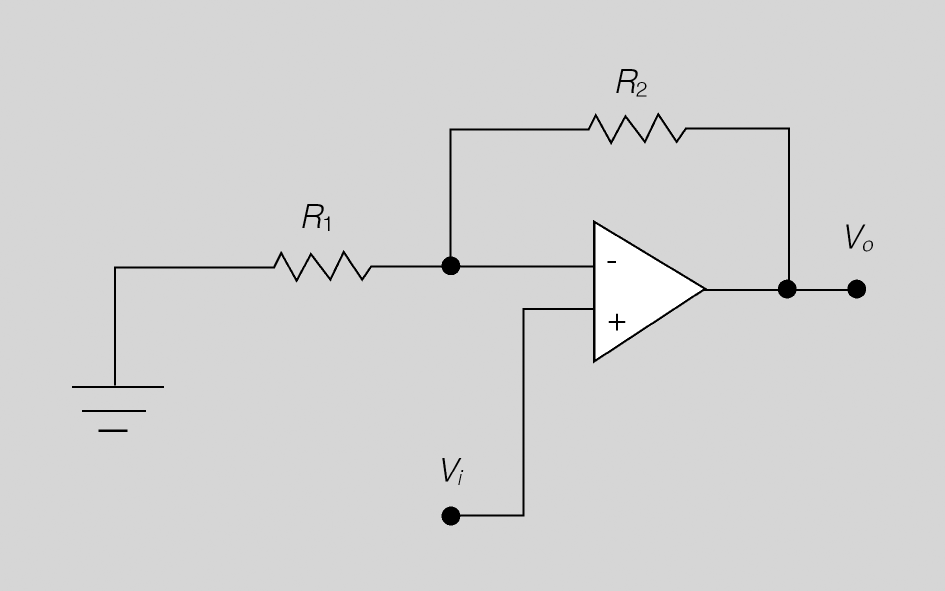
Amplificador no inversor
Exactament igual que el circuit inversor, el guany és determinat per les dues resistències d’acord amb la fórmula, però la tensió de sortida està en fase amb la tensió d’entrada, és a dir, no està invertida (figura).
L’amplificació de l’amplificador no inversor és:
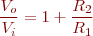
Exemple d'amplificador no inversor
Si R2 = 10 KΩ i R1 = 1 KΩ quin serà el guany del circuit? Si Vi = 1 mV, quin valor tindrà la sortida?
Solució:
Aplicant la fórmula del guany:
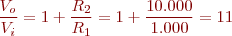
La tensió de sortida serà:


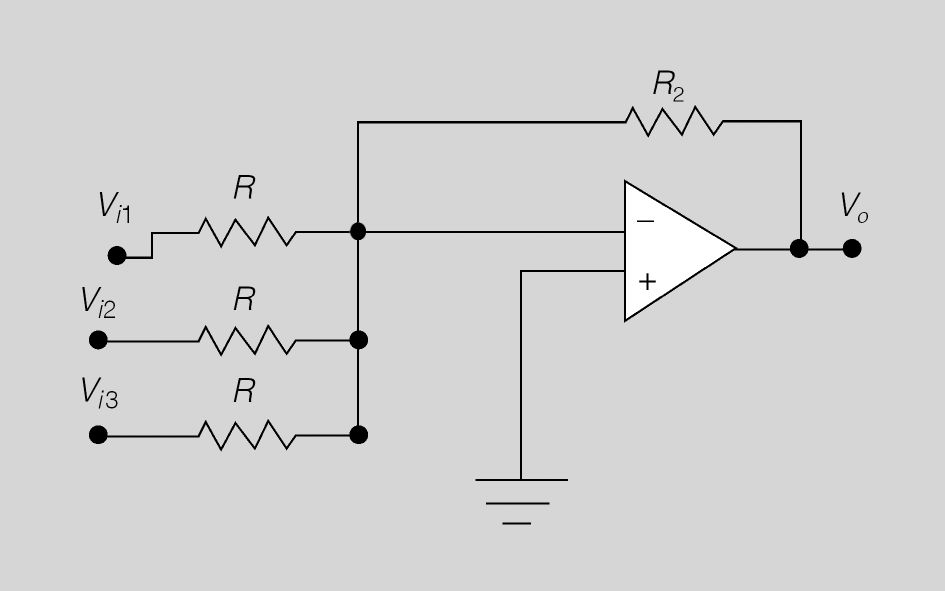
Amplificador sumador
L’amplificador sumador, tal com podeu veure en la figura, realitza la suma d’una sèrie d’entrades Vi1, Vi2, Vi3, … Vin, on n pot ser un número qualsevol, és a dir, el circuit podria tenir tantes entrades com vosaltres volguéssiu.
La sortida de l’amplificador sumador es:
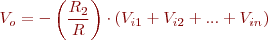
Si observeu atentament el circuit sumador, us adonareu que correspon a l’esquema d’un inversor però amb més entrades. D’aquí el signe menys de la sortida.
El guany és determinat pel valor de R2 i de la resistència R, que ha de tenir el mateix valor per a totes les entrades (condició indispensable per a què tots els senyals d’entrada siguin amplificats al mateix nivell).
Exemple de sumador
Si R2 = 10 KΩ i R = 1 KΩ quin serà el guany del circuit? Si Vi1 = 1 mV, Vi2 = 3 mV i Vi3 = 7 mV, quin valor tindrà la sortida?
Solució:
Aplicant la fórmula del guany:

La tensió de sortida serà:


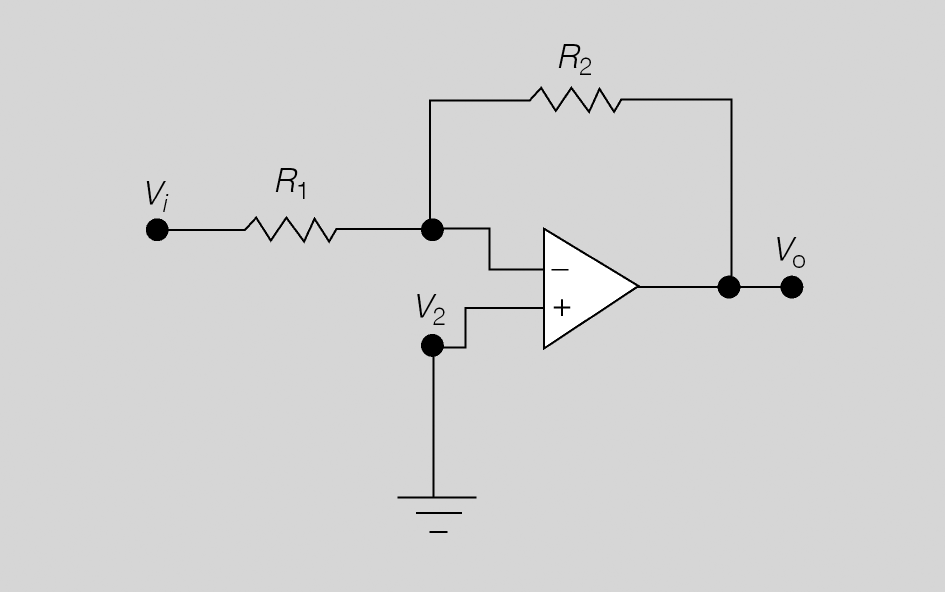
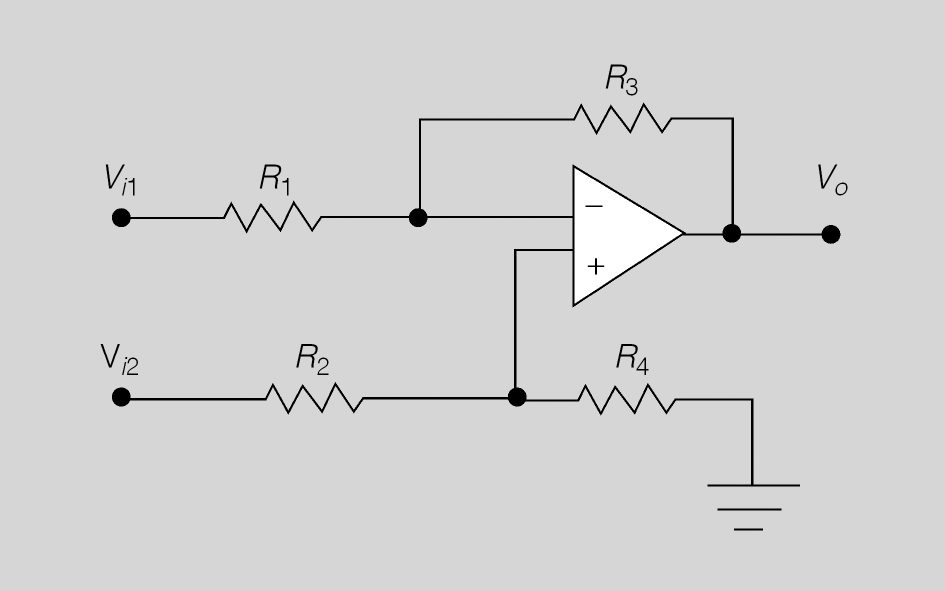
Amplificador diferencial
L’amplificador diferencial és molt utilitzat en instrumentació, en circuits de mesura de temperatures, de pes, deformacions, etc. La seva estructura es pot entendre com l’afegit de l’estructura no inversora i de l’estructura inversora. L’únic requisit és que ambdues estructures tinguin el mateix guany (figura).
Amplificador diferencial:
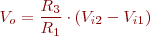
El circuit de la figura amplifica la diferència (resta) de dues tensions d’entrada (Vi2 − Vi1) d’acord amb la fórmula, sempre que es compleixi el producte de resistències següent:

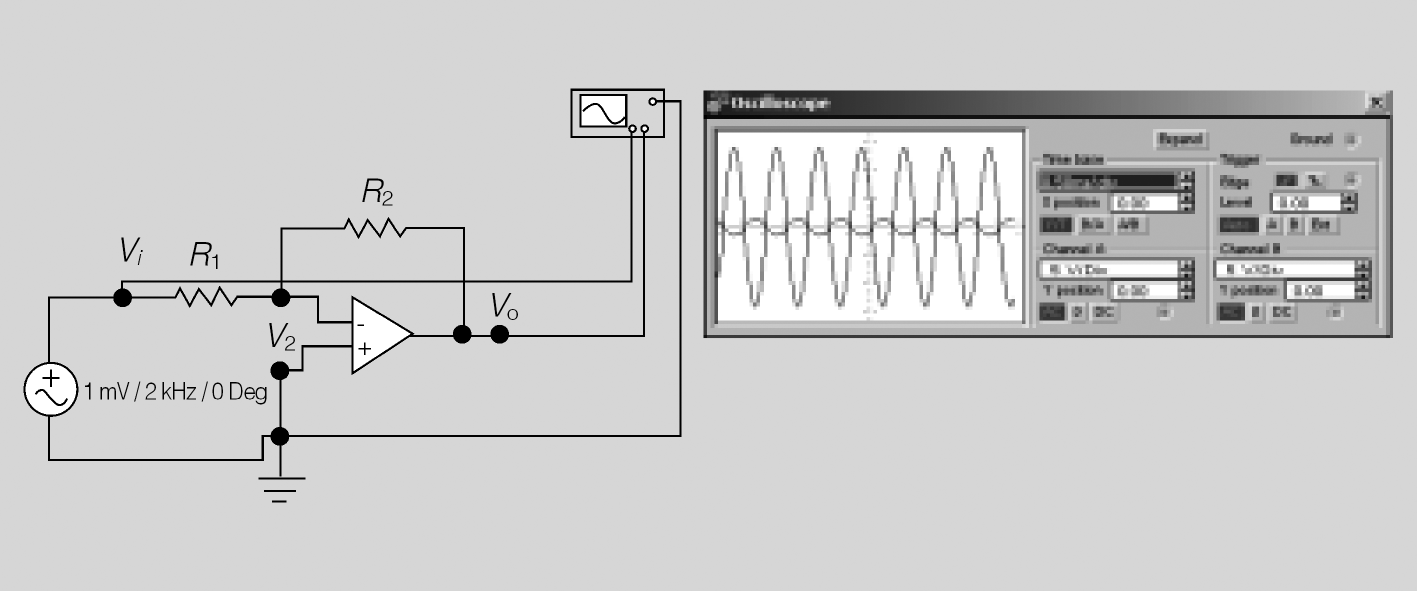
Exemple d'amplificador diferencial
Si R4 = R3 = 10 KΩ i R2 = R1 = 1 KΩ quin serà el guany del circuit? Si Vi1 = 1 mV i Vi2 = 3 mV, quin valor tindrà la sortida?
Solució:
Aplicant la fórmula del guany:

La tensió de sortida serà:


Aplicacions bàsiques amb dispositius integrats
Els amplificadors operacionals no serveixen només per fer sumes i restes de senyals, sinó que n’existeix un gran ventall d’aplicacions ben diverses, i no només de caire matemàtic, com es podria desprendre del nom del dispositiu. Així, entre moltes d’altres aplicacions, podríem parlar de:
- Amplificadors logarítmics
- Integradors
- Derivadors o diferenciadors (no confondre amb els amplificadors diferencials)
- Filtres actius (filtres amb amplificació)
- Portes digitals (per a això no s’usen perquè hi ha elements millors, però es podria)
- Convertidor de senyals
- Oscil·ladors i generadors de senyal
Algunes de les aplicacions citades són poc freqüents, però d’altres d’elles són ben importants en molts àmbits.
Integrador i derivador
Si observeu el circuit de la figura, podeu veure que s’aplica un senyal quadrat a l’entrada del circuit, i a la sortida s’obté un senyal triangular. El circuit realitza la conversió d’un senyal quadrat a un de triangular.
El circuit de la figura realitza el pas contrari, és a dir, a la seva entrada s’introdueix un senyal triangular i a la seva sortida s’obté un senyal quadrat.
Aquests dos circuits s’utilitzen habitualment per realitzar generadors de senyals.
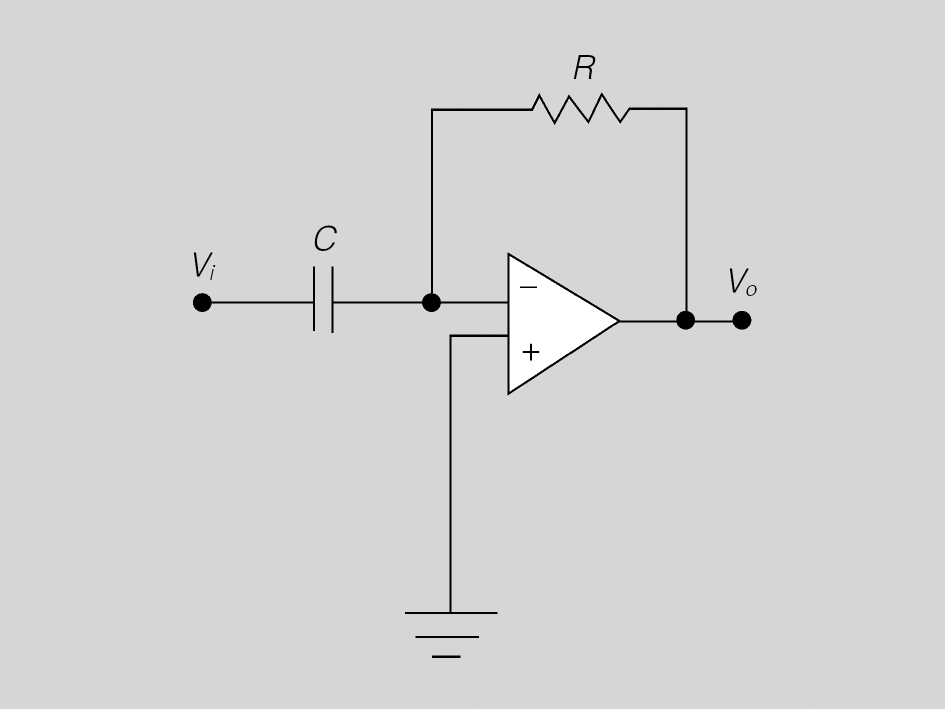
En termes estrictament matemàtics, el circuit de la figura dóna a la sortida la derivada de la funció que té a l’entrada, d’aquí el seu nom.
Anàlegament al derivador, el circuit de la figura es diu integrador perquè en termes matemàtics el que fa és calcular la integral de la funció que té a l’entrada. La integral és l’operació recíproca o inversa de la derivada, per això un circuit pot desfer el que fa l’altre.
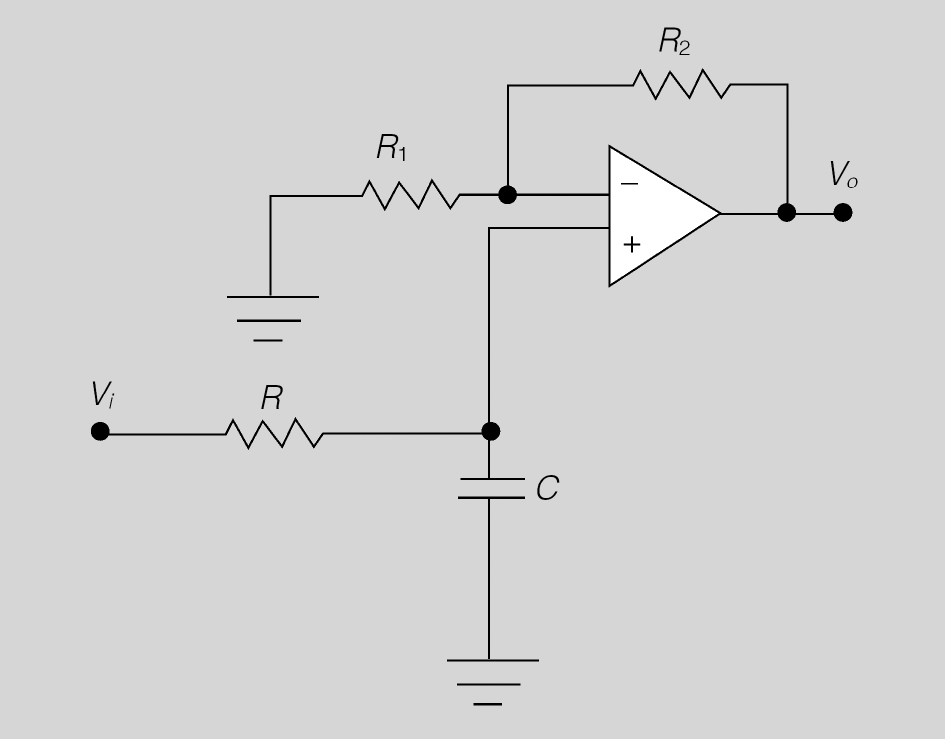
Filtre passabaix
El circuit de la figura és un amplificador no inversor. Si l’observeu, s’ha afegit una xarxa RC a l’entrada, que realitza la funció de filtre passabaix. És a dir, el circuit amplificarà sempre que la freqüència del senyal d’entrada estigui compresa dins l’amplada de banda del circuit. Com que és un filtre passabaix, la freqüència inferior és 0 Hz i la freqüència superior és determinada per R i C. Com que és un filtre passabaix BW = Fs − 0 = Fs.
Les expressions de la freqüència superior, guany i sortida són, respectivament:

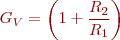
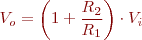
Ús dels filtres
Els filtres s’utilitzen per seleccionar un o diversos senyals d’entre molts o per eliminar interferències en un circuit; podeu trobar filtres en instal·lacions d’antenes, televisions, vídeos, receptors de ràdio (FM i AM), etc.
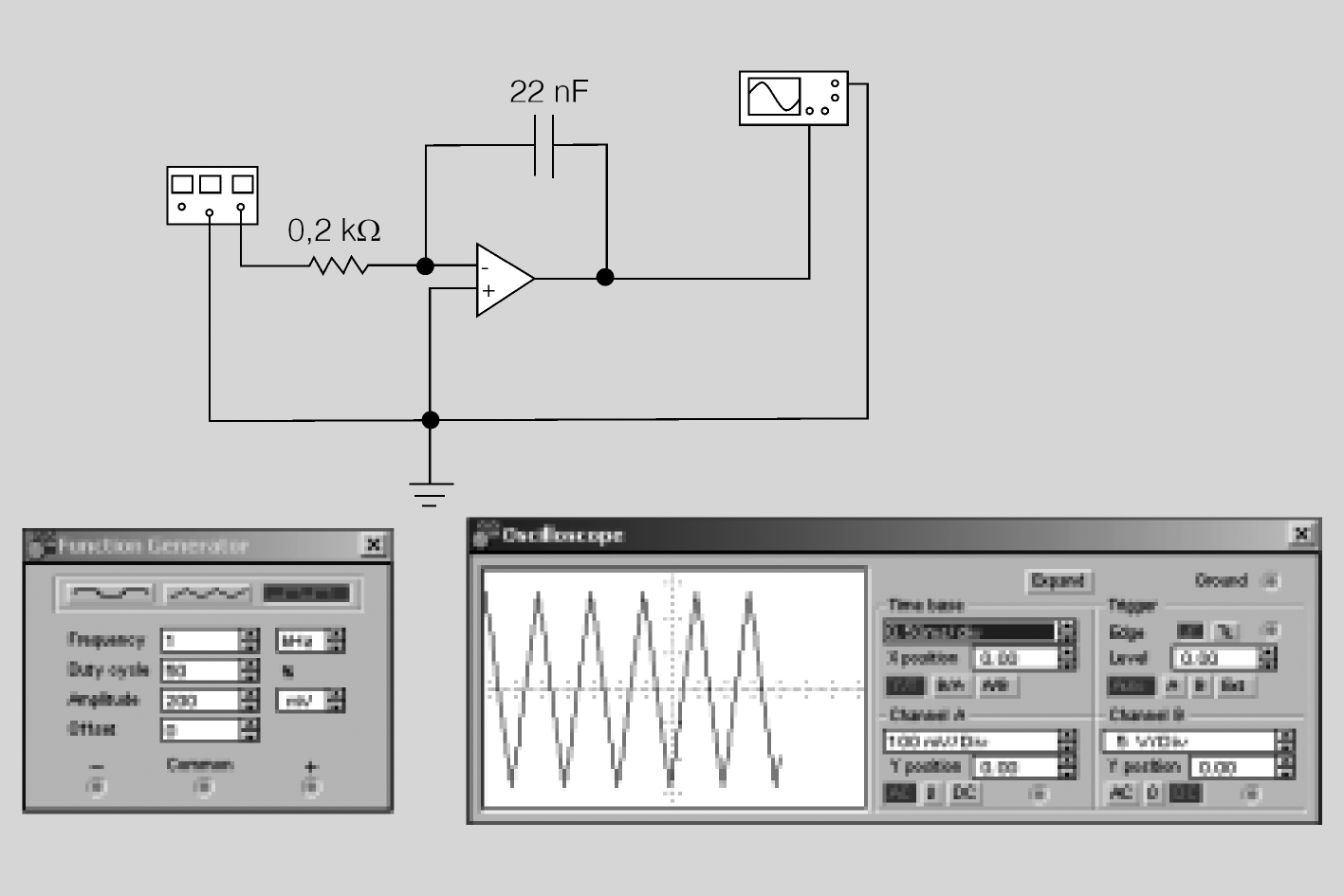
Exemple de filtre passabaix
Teniu un filtre passabaix amb AO amb els valors següents: R1 = 10 kΩ, R2 = 20 kΩ, R = 1 kΩ i C = 22 nF. Calculeu:
a) El guany i el BW.
b) Si introduïu un senyal Vi = 1 mV a 2 kHz, quin valor tindria Vo?
c) Si introduïu un senyal Vi = 5 mV a 10 kHz, quin valor tindria Vo?
Solució:
a) En primer lloc, calculeu el guany i la Fs.
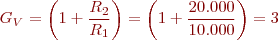

L’amplada de banda és BW = Fs = 7,3 kHz. Això vol dir que el circuit només funciona com a autèntic amplificador a dins del marge entre 0 i 7,3 kHz.
b) En aquest apartat, la Vi té una freqüència de 2 kHz, per tant, es troba dins del marge d’amplificació, la sortida serà:

c) En aquest apartat, la Vi té una freqüència de 10 kHz, es troba fora del marge d’amplificació. Per tant, idealment a la sortida no tindreu cap tipus de senyal: Vo = 0 (això no és ben bé així, però es pot considerar així en primera aproximació).
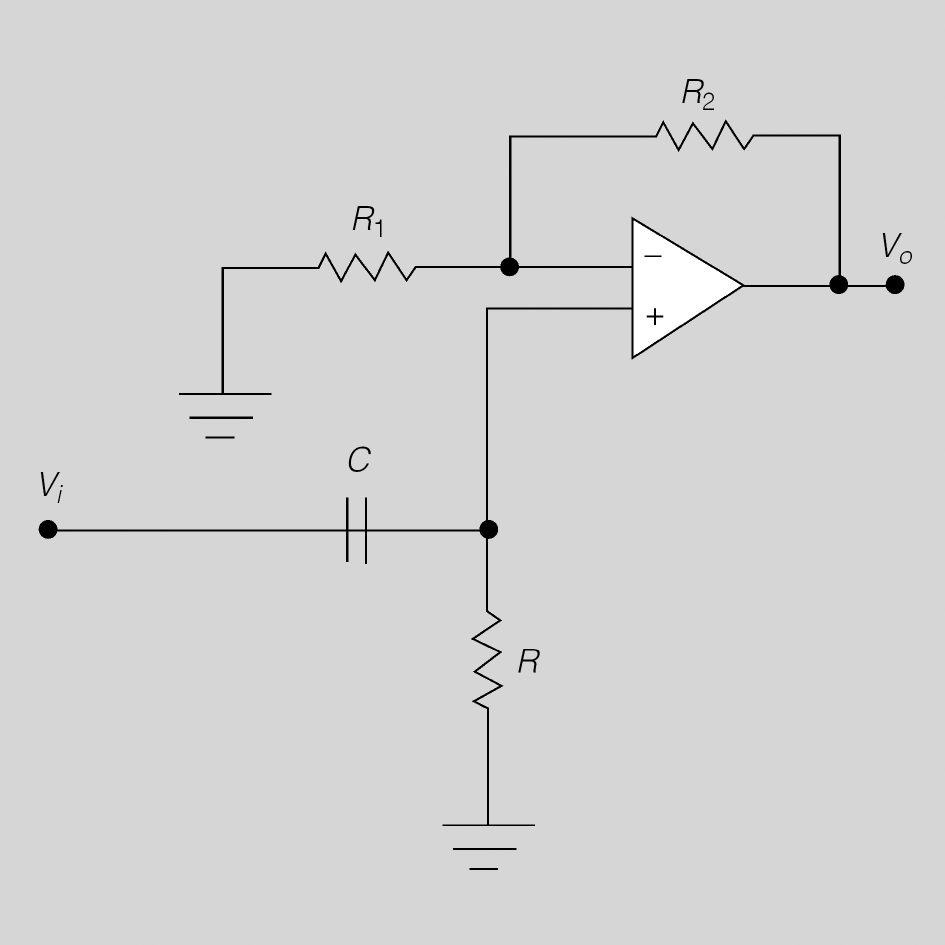
Filtre passaalt
El circuit de la figura és el mateix que d’un circuit passabaix, l’únic que s’ha canviat és la xarxa RC.
En aquest cas, el circuit es comporta com un filtre passaalt, és a dir, el circuit amplificarà el senyal d’entrada sempre que la freqüència d’aquest sigui superior a Fi. El valor de Fi s’obté dels valors de R i de C, anàlogament a com es feia amb el filtre passabaix. La seva expressió, juntament amb les de guany i sortida, són:

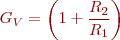
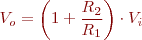
Filtre de pas de banda
Connexió en cascada
Es diu que una sèrie de circuits estan connectats en cascada quan s’interconnecten entre si de manera que la sortida d’un circuit ataca l’entrada del següent, i així successivament. En general, la sortida del sistema global es pot calcular aplicant successivament els guanys de cadascuna de les etapes, un rera l’altre.
Un filtre de pas de banda (figura) no és res més que un filtre passaalt connectat en cascada amb un filtre passabaix. Amb el primer filtre determineu la Fi i amb el segon, la Fs.
Com que són dos amplificadors connectats en cascada, el guany total (GVt) del circuit s’obté del producte dels dos guanys, on GV1 és el guany de la primera etapa i GV2 és el guany de la segona etapa. Les fórmules que caracteritzen aquest filtre són:




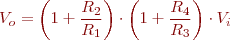
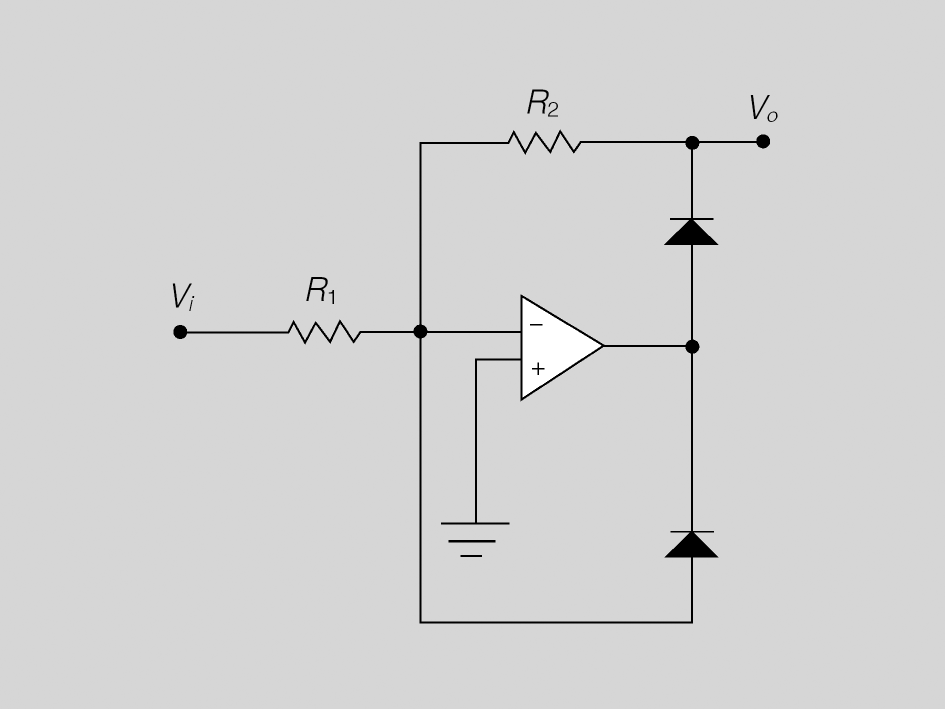
Altres circuits
Amb l’amplificador operacional es poden realitzar una quantitat molt elevada de circuits amb diferents funcions o finalitats, com per exemple un rectificador com el de la figura.
En el circuit de la figura rectifica el senyal Vi, que pot ser d’un valor petit (de l’ordre dels mV), i a la sortida s’obté una Vo rectificada i amplificada, on el guany de tensió és determinat per:
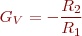
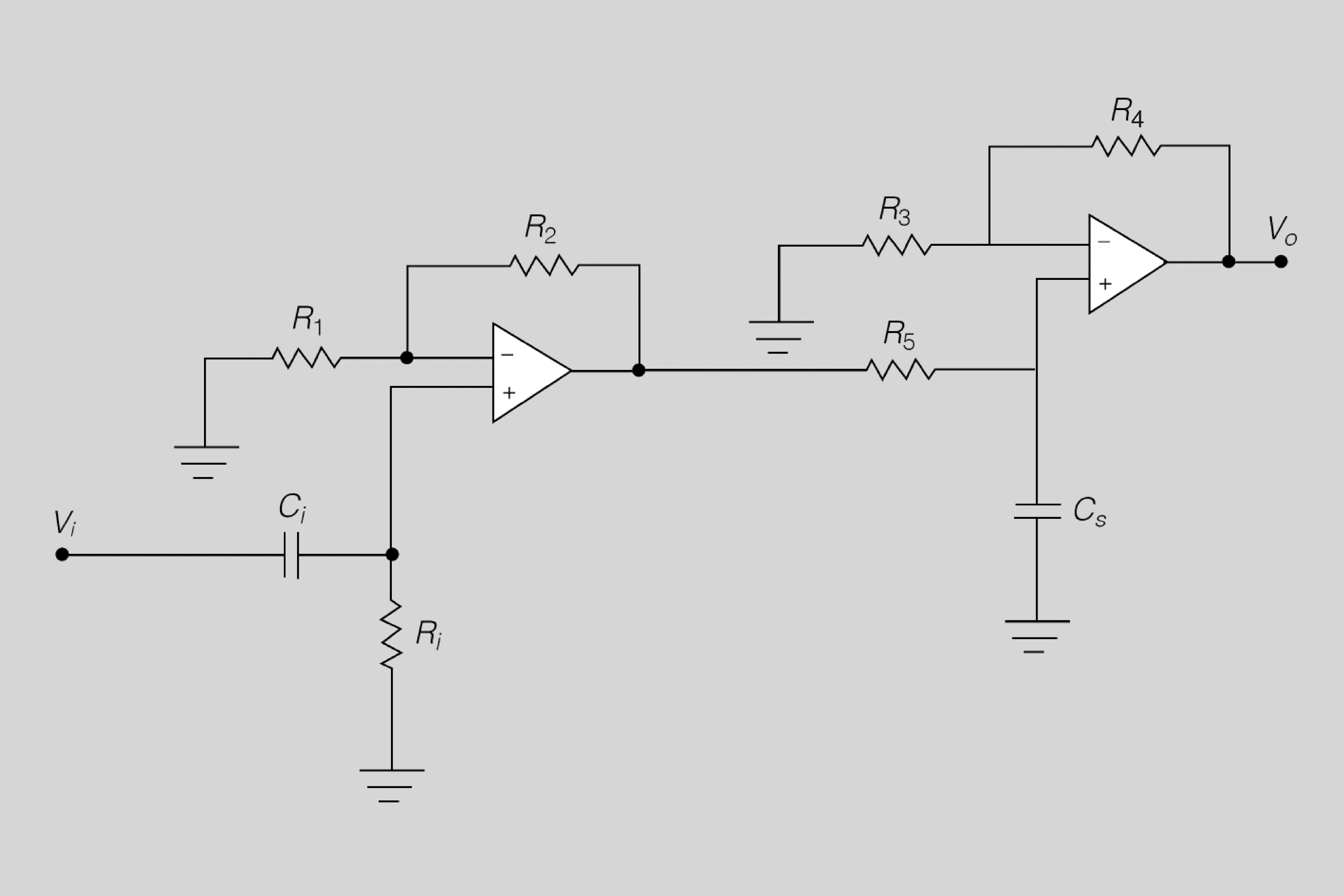
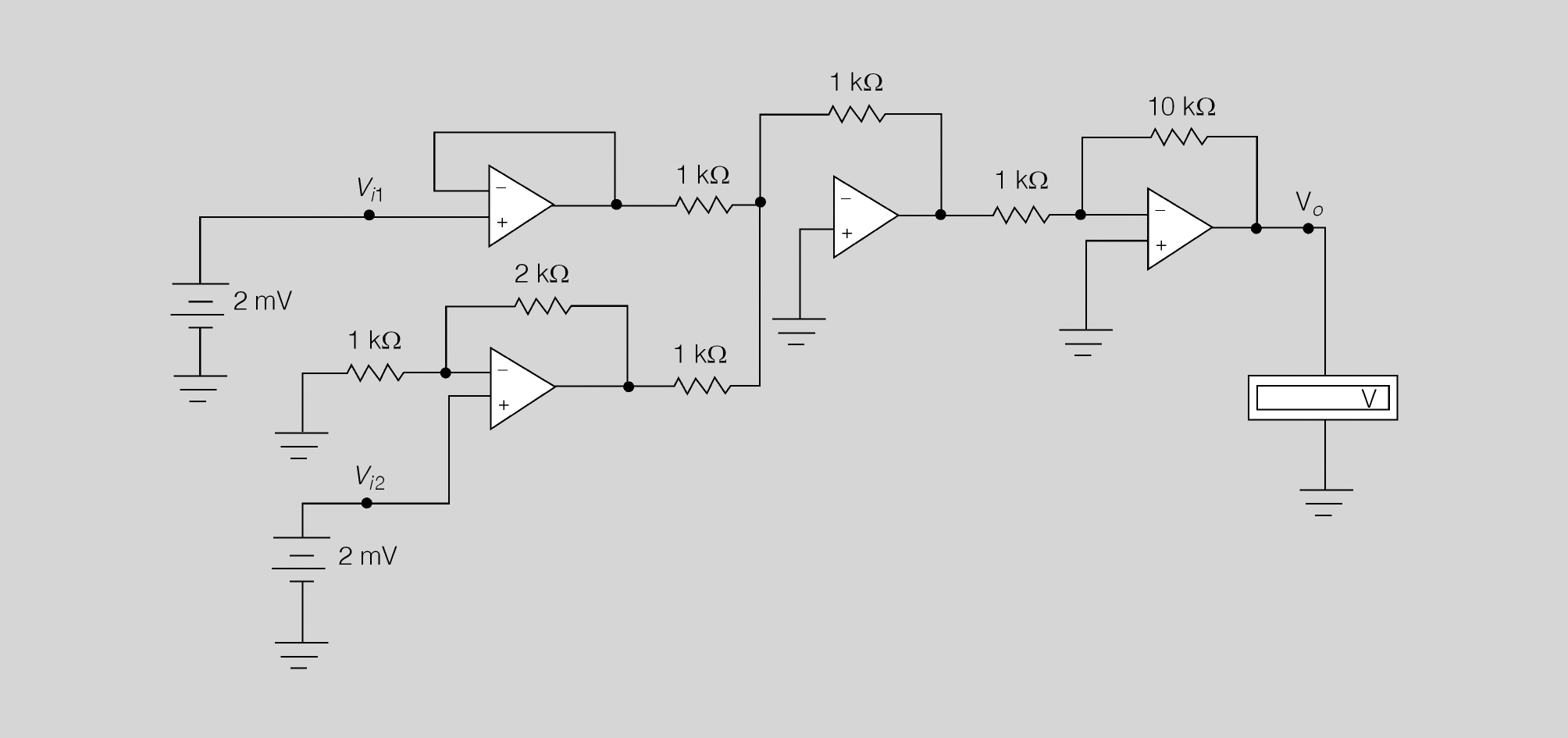
A l’hora d’interpretar esquemes us trobareu amb circuits com els de la figura, a on s’observa l’existència d’un conjunt d’etapes interconnectades. A l’esquema, cada AO realitza un funció concreta que ha de ser identificada.
Exemple de circuit genèric amb AO
Per al circuit de la figura, calculeu el valor de la tensió de sortida.
Solució:
Per poder trobar el valor de la Vo, el primer que s’ha de fer és identificar cadascun dels AO:
- L’entrada Vi1 està aplicada a un AO seguidor de tensió.
- La sortida d’aquest seguidor ataca un AO sumador.
- La sortida del sumador està connectada a un amplificador inversor.
Observeu ara l’entrada Vi2:
- Està connectada a un amplificador no inversor.
- La sortida d’aquest nop inversor és l’altra entrada de l’AO sumador.
Amb els valors del circuit, trobareu ara el valor de la Vo:
- La sortida del seguidor és igual a Vi1 = 2 mV.
- La sortida del no inversor és igual a 6 mV.
- La sortida del sumador amb les seves dues entrades de 2 mV i 6 mV és igual a −8 mV.
- Finalment, l’entrada de l’amplificador inversor és de −8 mV, i per tant, aplicant la fórmula, teniu que Vo = 80 mV.