|
||||||||||||||||
| Pràctica |
|
Exercicis
|
||||||||||||||
| Idees sobre estimació. Estimació d'una proporció |
Glossari
|
|||||||||||||||
|
El teorema del límit central. Estimació d'una mitjana |
||||||||||||||||
| El teorema del límit central: visió empírica | |
|
L'objectiu d'aquesta pràctica és fer simulacions amb el programa Excel a partir de diverses poblacions teòriques i analitzar la distribució de les mitjanes mostrals per constatar empíricament el teorema del límit central. 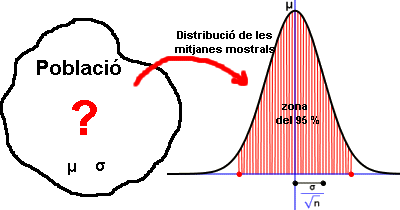 Una imatge per recordar el teorema
del límit central
|
|
|
|
|
|
|
Simulacions a partir d'una població normal |
|
En aquesta primera part de la pràctica, fareu simulacions de la selecció de mostres a partir d'una població que segueixi el model normal per constatar empíricament la versemblança del teorema del límit central. Posteriorment, es proposarà que repetiu uns procediments semblants, però a partir d'una població que correspongui al model uniforme continu per copsar la idea que les característiques de la població de partida no són transcendentals per a l'estimació d'una mitjana. Plantejament: Si suposem que en una població
teòrica els valors d'una variable X es distribueixen d'acord amb
un model normal de mitjana En aquesta pràctica:
Tot seguit, s'explica com es pot portar a terme aquesta activitat: |
|
Si ho heu fet així, en el full actiu s'han generat, a les 200 primeres columnes (de la A a la GR), 200 mostres de mida 100. No hi posarem títols. Cada mostra ocupa una columna diferent. Nota important: Si esteu treballant amb la versió 97, aquest procés s'haurà fet incorrectament (i no per culpa vostra!). Per comprovar-ho, seleccioneu la cel·la L23 i observeu que ha aparegut el nombre 6250005, que, evidentment no hauria d'haver sortit! Aquest nombre surt en tres cel·les més (EL51, ES17 i FB72). Això es deu a un funcionament anòmal de l'Excel 97 en aquest aspecte. Hem comprovat, que en aquest cas, el nombre que surt en aquestes cel·les en la versió 2000 és 11,70552225. Per tant, us proposem que, per poder seguir la pràctica, substituïu un nombre per l'altre. Ho podeu fer automàticament accedint a Edición | Reemplazar. Tot seguit entreu el nombre 6250005 en l'apartat de Buscar i el nombre 11,70552225 en l'apartat Reemplazar con. A continuació premeu Reemplazar todas. Els autors pensem que en la resta de la pràctica no trobareu problemes però com que es tracta d'un funcionament anòmal de la generació de nombres aleatoris és impossible assegurar que aquesta sigui l'única anomalia que es presenti.
|
|
| Ja havíem vist
que teníem un bon ajust de la mitjana i la desviació estàndard de la distribució
de mitjanes mostrals amb els valors establerts pel teorema del límit central.
Però, aquest ajust és vàlid també per a tot el model normal? El gràfic obtingut
a la pràctica anterior mostra que sí!
I si voleu fer altres proves numèriques i constatar l'extraordinària precisió del teorema del límit central (cosa que us recomanem), accediu al full on heu fet les simulacions i torneu a activar Herramientas | Análisis de datos | Generación de números aleatorios | Normal, deixeu els mateixos paràmetres definidors de la població (la distribució normal a partir de la qual es genera una mostra) i el mateix rang de sortida. Canvieu el nombre enter de Iniciar con... (o deixeu-ho sense cap nombre, i llavors cada simulació donarà valors diferents) i observeu l'evolució dels valors a les files 104 i 106 que l'Excel actualitza automàticament en cada nova simulació. | |
|
|
I si partim d'una població que no segueix el model normal? |
|
Si la població de partida segueix el model normal, el teorema del límit central és, estrictament, un teorema, demostrable per formulacions matemàtiques que s'escapen dels objectius d'aquest curs. Tanmateix, encara que la població de partida segueixi un altre
model (o no coneixem quin és el possible model que li podem aplicar),
llavors hi ha una aproximació empírica que ens diu que si
la mida de la mostra és suficientment gran (n Enunciat: Si recollim mostres de mida
100 d'una població i analitzem els valors d'una variable X, llavors
la mitjana mostral de la variable X es pot modelitzar amb un altíssim
grau d'aproximació mitjançant una distribució normal de mitjana
En aquesta segona part de la pràctica, ho constatarem amb un exemple, a partir de la distribució uniforme.
Aneu fent diverses proves, cada vegada amb la simulació de 200 mostres de mida 100, i comprovareu que, efectivament, encara que la població de partida no sigui normal, l'ajust que estableix el teorema del límit central és excel·lent.
Com a exercici opcional d'aquest mòdul, podeu enviar un comentari i resultats d'aquesta part de la pràctica. |
|
| Ampliacions, aclariments i comentaris | |
|
|
Una prova de consistència
del model Segur que algunes i alguns penseu: "Però l'ull i la intuïció poden enganyar". Llavors, com podríeu constatar amb una prova estadística que el model normal observat per a la distribució de mitjanes mostrals és consistent? En els tractats d'estadística, hi ha moltes i diverses proves de normalitat, però, com ja s'ha comentat al mòdul 6, no estan incorporades a l'Excel. Tanmateix, ara que teniu unes freqüències observades i unes freqüències esperades, podríeu fer servir la prova de khi quadrat? A la pràctica 5 del mòdul 6 ja hem comentat aquest procediment com una possibilitat ben certa. En aquest cas, podeu provar d'aplicar khi quadrat i veureu que tant amb les classes que ja teniu definides com amb d'altres que pugueu definir, el valor p sempre és molt alt: hi ha criteris estadístics molt sòlids per admetre la consistència del model normal per a la distribució de les mitjanes mostrals. Per tant, podeu veure que en aquest cas, el fet que la tria de les classes aporti una càrrega subjectiva que pot condicionar molt el resultat de la prova no és del tot cert: el model normal està molt i molt ajustat a les dades. I si algú dubta, encara pot provar d'aplicar el test de Kolmogorov-Smirnov! |