|
|
Analitzarem pel procediment indicat (àmpliament comentat al document
teòric que convé que hagueu llegit abans de la pràctica) la variable
ALT3 del full de dades del llibre DADES74.XLS i veurem que, tot
i que en principi se'ns podrien presentar dubtes pel fet d'haver-hi dues
subpoblacions ben diferenciades (les noies i els nois), finalment la conclusió
serà la d'acceptar el model normal.
Val a dir que s'ha escollit aquesta variable per dur a terme aquesta
pràctica en part pel nombre de dades que recull (110), perquè amb un nombre
sensiblement inferior de dades la prova de khi quadrat no és gaire recomanable
(recordeu la condició que la freqüència esperada en cada classe ha de
ser superior a 5) i amb aquest nombre de dades i el nombre de classes
que convindrà fer serà molt visual tot el procediment.
- Obriu el llibre DADES74.XLS i podeu inserir-hi un nou full
en blanc.
- Al full Dades74 seleccioneu tota la columna J, la de la variable
ALT3, i feu Control + C.
- Recupereu el full nou que heu obert i a la cel·la A1 feu Control
+ V.
- Escriviu a la cel·la B1 Classes. Ara definirem en aquesta columna
les classes per agrupar les dades. Vist que el valor mínim és 154 i
el màxim 192 i que ens interessa que es decideixi clarament a quina
classe va cada valor, escriurem a B2:B8 els valors 157,25; 162,25; 167,25...;
187,25 i amb això les classes seran, en principi, les següents:
menys de 157,25
(157,25; 162,25)
(162,25; 167,25)
...
(182,25; 187,25)
més de 187,25
- Deduirem els paràmetres del model normal amb què volem confrontar
les dades a partir de les pròpies dades. Escriviu a la cel·la C1 Mitjana
i a la cel·la C3 Desv. est. i llavors a les cel·les C2 i C4 els
valors corresponents: =PROMEDIO(A2:A111) i =DESVEST(A2:A111). Es pot
pensar si cal fer servir la funció DESVEST, el paràmetre inferencial,
o bé DESVESTP. Estem fent una inferència? Efectivament: volem contrastar
la hipòtesi que el conjunt de dades recollides prové d'una població
que segueix el model normal. Com que fem una hipòtesi sobre la població,
escau millor DESVEST.
- En primer lloc, cal que analitzem les freqüències esperades en cada
classe per la distribució normal que té la mitjana i desviació estàndard
que acabem de calcular. Escriviu a D1 Probabilitats, i llavors
les fórmules escaients són:
- A D2, =DISTR.NORM(B2; $C$2;$C$4; 1). Vegeu que amb això estem
calculant la probabilitat acumulada fins a 157,25.
- A D3, =DISTR.NORM(B3; $C$2;$C$4; 1) – DISTR.NORM(B2; $C$2;$C$4;
1) i convenceu-vos que així realment calculem la probabilitat de
la classe (157,25; 162,25).
- Copieu la fórmula anterior al rang D4:D8.
- Finalment, a D9, la fórmula = 1 – DISTR.NORM(B8; $C$2;$C$4;
1) ens dóna la probabilitat de més de 187,25.
- Escriviu a la cel·la E1 Freq. esp. i llavors, naturalment,
per calcular les freqüències esperades, escriviu a E2 la fórmula =D2*110
i copieu aquesta fórmula a tot el rang E3:E9.
- Veureu que la classe més de 187,25 no compleix la condició
que la freqüència esperada sigui 5 o més. Cal ajuntar les dues darreres
classes i fer que la darrera sigui més de 182,25. Per aconseguir-ho:
- Copieu la fórmula que fa la probabilitat de la darrera classe
de D9 a D8 (perquè ara hem de calcular la probabilitat de més de
182,25).
- Ara ja podeu esborrar la cel·la B8 (ja
no fem servir el 187,25), la cel·la D9 (on
es calculava la probabilitat de més de 187,25, que era el valor
que teníem a D8) i la cel·la E9.
Ara ja tenim totes les classes amb la freqüència esperada més gran que
5.
- Per calcular les freqüències observades podeu fer servir, com s'indica
seguidament, el procediment Herramientas | Análisis de datos | Histograma:
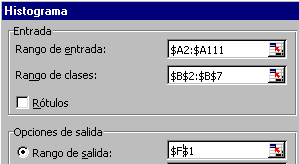
Observeu que, tot i que al quadre de diàleg de l'histograma hem
posat com a rang de classes B2:B7, després hi ha una classe més (la
que correspon a més de 182,25) i veureu que les freqüències
observades queden, tret d'un títol a G1, al rang G2:G8.
- Ara podeu tenir una primera idea del valor p del conjunt de dades
si escriviu a la cel·la H1 valor p i a la cel·la H2 la fórmula =PRUEBA.CHI(G2:G8;
E2:E8) (amb el benentès que si no teniu ben clara la sintaxi llavors
Insertar | Función | PRUEBA.CHI us recordarà que és PRUEBA.CHI(rango_actual;
rango_esperado)). Veureu un valor p molt gran, 0,39, que us indica que
no es pot dubtar de manera consistent del model normal (gran risc d'error
si es rebutja la hipòtesi nul·la de normalitat).
- Però en realitat, hem deduït dos paràmetres a partir de les dades.
Ja es va explicar en el seu moment que si volem actuar amb tot rigor,
aquesta deducció implica que el test de khi quadrat s'ha d'aplicar amb
dos graus de llibertat menys del que ho ha fet per se el programa
Excel.
Calculeu l'estadístic X2 i apliqueu la prova amb 4 graus
de llibertat
(7 classes – 1 com és habitual – 2 pels paràmetres deduïts).
Ja s'ha explicat en pràctiques anteriors el procediment:
- Escriviu a I1, per exemple, Sumands o un altre rètol explicatiu.
- Escriviu a I2 la fórmula =(G2-E2)^2/E2.
- Copieu aquesta fórmula perquè sigui vàlida en tot el rang I2:I8.
- A la cel·la J1 escriviu Estadístic i a J2 poseu la fórmula
=SUMA(I2:I8).
- A la cel·la J3 escriviu Valor p corregit i a J4 poseu =DISTR.CHI(J2;
4). Veureu que el valor p obtingut, 0,18, encara és prou alt per
acceptar sense cap recança el model normal. (Si
a la cel·la J4 haguéssiu posat la fórmula DISTR.CHI(J2; 6), hauríeu
obtingut el mateix valor p 0,39 que teniu a H2, però calia baixar
en 2 el nombre de graus de llibertat, de 6 a 4, pel fet d'haver
deduït dos paràmetres a partir de les dades.)
Tot seguit, us proposem que refeu els càlculs, però amb unes classes
més petites. Ara prendrem com a semirectes la inicial i la final, i com
a intervals de longitud 2,5 les altres.
Anteriorment, hauríem pogut procurar muntar el procediment de l'Excel
perquè servís encara que anés canviant el nombre de dades –no és
el cas– o el nombre de classes, però això potser ens faria apartar
del que interessa en aquesta pràctica, que és entendre els procediments
per fer una prova de normalitat.
- Els autors hem fet la prova amb les classes definides per 157,25;
159,75...; 182,25 i, després d'analitzar les freqüències esperades,
hem vist que cal ajuntar les dues primeres classes. Per tant, aprofiteu
aquesta dada i escriviu a la columna B com a límits definidors de les
classes els valors 159,75; 162,25; 164,75... i ja els podeu ampliar
per arrossegament fins a 182,25, que queda a la cel·la B11.
- Per calcular les probabilitats, i a partir d'elles les freqüències
esperades, tingueu cura de copiar la fórmula que comença 1 – DISTR.NORM...
(la que teniu a la darrera cel·la operativa de la columna D, que és
la que calcula la probabilitat esperada en la darrera classe, més
de 182,25) a la cel·la D12. Després, feu que la que teniu a D3 sigui
vàlida en tot el rang D3:D11. La que teniu a D2 ja és vàlida igualment.
- Ara que ja teniu correctament calculades les probabilitats, feu que
la fórmula que teniu a E2 sigui vàlida en tot el rang E2:E12.
- Torneu a activar Herramientas | Análisis de datos | Histograma,
però modificant adequadament el rang on estan indicades les classes
(B2:B11); ara, les freqüències observades queden a G2:G12.
- Modifiqueu la fórmula de H2 perquè digui =PRUEBA.CHI(G2:G12; E2:E12);
el valor p que surt, de l'ordre de 0,11, ens diu que fins i tot amb
aquestes classes, ben petites, es pot acceptar la consistència del model.
- Però si fem el càlcul dels sumands de l'estadístic (per les files
de la 2 a la 12) i calculem el valor p corregit i apliquem la prova
amb 11 – 1 – 2 = 8 graus de llibertat, llavors el
valor p no arriba a 0,05. Podem començar a dubtar del model.
Quin és el criteri que hem de seguir?
- En l'exemple anterior, classes d'amplada 5 o classes d'amplada 2,5?
Recordeu que en principi es guanya informació com més petites són
les classes, però... no podria ser que haguéssim exagerat? (Penseu que
si arribéssim a classes de longitud 1, ja estaríem treballant dada a
dada amb un procediment que té com a quid l'agrupació en classes!)
- Hem de restar els dos graus de llibertat per haver deduït dos paràmetres,
o no? Adoneu-vos que si plantegéssim el problema dient:
"Un estudi estadístic anterior afirmava que les alçades
d'alumnes de 16 anys, nois i noies conjuntament, seguia una distribució
normal de 170 cm de mitjana i desviació estàndard de 7,6. El conjunt
de les dades recollides en el fitxer DADES74, concorda amb
aquest model?"
...hauríem de fer exactament els mateixos càlculs, resultaria un valor p gran i no seria necessari restar els 2 graus de llibertat.
De fet, aquestes consideracions les hem deixat expressament en suspens,
perquè no tenen una resposta unívoca. L'aplicació de la prova de khi quadrat
per a un test de normalitat, sempre té una càrrega subjectiva. Per aquesta
raó, es defineixen i es recomanen altres tipus de proves com la que veurem
al segon apartat d'aquesta pràctica.
|
|
|
Vegeu la descripció de la prova a la teoria.
En aquesta part de la pràctica s'exposa la manera d'aplicar la prova
per a conjunts de més de 35 dades i amb un nivell de significació del
5 %, atenent al fet que en aquest cas tenim un valor asimptòtic donat
per la fórmula 1,36/RAIZ(n), en què n és la mida
de la mostra estudiada. Si el nombre de dades fos més petit, o bé el nivell
de significació fos un altre, només caldria que canviéssiu del procediment
que s'explicarà tot seguit el punt que compara el valor de l'estadístic
observat amb el valor crític que es pot llegir a la taula, i així es pot
respondre passa el test o bé no passa el test.
Aplicarem la prova per a la mateixa variable que en el cas anterior,
ALT3 del full de dades del llibre DADES74.XLS.
- Una vegada hagueu obert el llibre indicat, inseriu-hi un full nou
per fer els càlculs.
- Recupereu el full Dades74, seleccioneu tota la columna J on
teniu la variable ALT3 i feu Control + C.
- Enganxeu aquests valors (amb el rètol inclòs) a la columna A del full
nou, que podeu anomenar Kolmogorov.
- Per fer servir el mètode pràctic de càlcul de l'estadístic D
de Kolmogorov explicat al document teòric, ordeneu les dades d'aquesta
columna. Recordeu: Datos | Ordenar indicant que la columna té
rètol a la primera fila i que voleu les dades en ordre creixent o, en
aquest cas, també anirà bé amb la icona
 . .
- A la columna B escriviu a la cel·la B1 el rètol Núm. ordre
i al rang B2:B111 els nombres de l'1 al 110.
- Com heu fet amb el test de khi quadrat, a la columna C calculeu-hi
la mitjana i la desviació estàndard del conjunt de dades per establir
els paràmetres del model normal que prendrem com a referència. Escriviu
a la Mitjana, a C2, =PROMEDIO(A2:A111), a C3 Desv. est.
i, finalment, a C4 =DESVEST(A2:A111). Podeu afegir a C5 el rètol Mida
mostra i escriviu a C6 el nombre 110.
- A la columna D posareu els valors corresponents a la funció de distribució
teòrica de la normal de mitjana $C$2 i desviació estàndard $C$4. Escriviu
a D2 la fórmula =DISTR.NORM(A2;$C$2;$C$4; 1) i copieu-la per arrossegament
perquè sigui vàlida també al rang D3:D111.
- Ara calculeu en dues columnes diferents els valors absoluts de
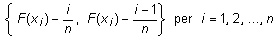
- A la columna E podeu posar el rètol ValorsD1 i, perquè
hi apareguin els valors que veieu en primer lloc en el conjunt anterior,
la fórmula adequada a la cel·la E2 (que després copiareu a E3:E111)
és = ABS(D2–B2/$C$6).
- A la columna F poseu el rètol ValorsD2; a F2 escriviu la
fórmula
= ABS(D2–(B2–1)/$C$6) i, finalment, al rang F3:F111 copieu-hi
la fórmula anterior.
- A la cel·la G1 escriviu Estadístic D i calculeu-lo a la cel·la
G2 amb la fórmula =MAX(E1:F111).
- Poseu a la cel·la G3 Valor crític i a la cel·la G4 aquest valor
mitjançant la fórmula =1,36/RAIZ($C$6).
- Per acabar, a la cel·la G5 escriviu Conclusió i a la cel·la
G6 la condició que ens diu si podem considerar consistent el model normal
o no:
=SI(G2 < = G4; "passa el test"; "rebutgem normalitat")
Podeu observar que, amb les dades estudiades, el test de Kolmogorov-Smirnov
accepta el model normal.
Ja s'havia comentat que aquesta prova era molt tolerant. I en aquest
cas, si voleu aplicar el test amb un nivell de significació del 10 % (agosarat,
tendiríem a rebutjar molt el model), i per fer-ho canvieu la fórmula de
la cel·la G4 per =1,22/RAIZ($C$6) com indica la taula
corresponent, veureu que encara es passa la prova.
En el document teòric heu vist un gràfic
que fa visual la discrepància entre la funció de freqüències empíriques
acumulades (es mostren només els punts de salt) i la funció de distribució
del model teòric normal. Podeu consultar tot seguit com es pot fer aquest
gràfic:
- Des del full Kolmogorov en què treballeu, podeu activar Datos|Tablas
dinámicas. Indiqueu que el rang de valors en què
teniu les dades de què voleu fer la taula és $A1:$A111.
- En el disseny de la taula poseu a FILA el rètol de la variable
ALT3 i a Datos desplaceu-hi el mateix rètol i vigileu
que aparegui Contar de ALT3. Si no fos així, segurament
recordeu que ho podeu arreglar fent doble clic al rètol que hagi
quedat a la zona DATOS.
- Podeu indicar que voleu la taula en un full nou. Quan ja estigui feta,
la convertirem com ja hem fet altres vegades en una taula senzilla,
no dinàmica. Seleccioneu-la tota clicant al rètol Contar
de ALT3. Llavors feu Control + C i amb el rang de la taula
encara seleccionat feu Edición | Pegado especial | Valores.
Una vegada fet això, elimineu la fila o les files superiors
necessàries perquè els rètols ALT3 i Total
quedin a la primera fila, a les cel·les A1 i B1 respectivament.
Podeu eliminar també les dues últimes files, Vacías
i Total general.
- A partir de la segona columna, que és la columna de freqüències
absolutes, fareu la columna de freqüències relatives acumulades
(funció de ditribució empírica).A la cel·la
C1 d'aquest full nou escriviu, doncs, Freq. acum. emp. A la cel·la
C2 escriviu la fórmula
=SUMA($B$2:B2)/110
i copieu-la a tot el rang C3:C31. Reflexioneu per què (amb el benentès
que 110 és el nombre de dades) així s'ha obtingut la freqüència relativa
acumulada.
- Tot i que ja en teníem els valors, que hem fet servir per calcular
l'estadístic D de Kolmogorov, ara ens interessa recalcular
en una altra columna la funció de distribució (probabilitat
acumulada) de la distribució normal amb què ajustem les
dades (és que convé referir-la als valors que ara tenim
a la columna A). Necessitem la mitjana i la desviació estàndard.
Obriu el full Kolmogorov, seleccioneu el rang B1:B4 i feu
Control + C; tot seguit, torneu al full nou, en el qual s'ha situat
la taula, seleccioneu la cel·la D1 i feu Edición |
Pegado especial | Valores (o bé, alternativament a tot això,
podeu tornar a calcular la mitjana i la desviació estàndard
respectivament a les cel·les D2 i D4).
- Escriviu a la cel·la E1 Func. distr. teòrica.
La fórmula que escau a la cel·la E2 (que després
copiareu a E3:E31) és =DISTR.NORM(A2;$D$2;$D$4;1).
- Ara seleccioneu la columna A; amb la tecla de Control premuda
seleccioneu la columna C on teniu les freqüències relatives
acumulades empíriques; encara amb el Control premut, seleccioneu
també la columna E, en què acabeu d'obtenir la funció
de distribució acumulada teòrica.
- Obriu el procediment per fer gràfics i trieu Dispersión i el
primer subtipus de gràfic.
- Fixeu-vos en la llegenda. Indica segurament que les freqüències
empíriques estan indicades per punts blaus i les teòriques
per punts magenta, però ben segur que penseu que s'ha de
millorar, i molt. (Si per alguna circumstància
d'ús anterior de l'Excel i un possible canvi dels colors predeterminats,
en el vostre cas no són aquests els colors, heu de fer "una traducció".)
- Podeu començar per esborrar la llegenda.
- Tot seguit, heu d'adequar millor a les dades que teniu el Formato
de ejes | Escala. Poseu de 150 a 195 pel que fa a l'eix
de les x, i de 0 a 1 a l'eix vertical.
- Cliqueu sobre els punts de color magenta (que segurament se superposen
als blaus). Quan estiguin seleccionats, botó dret i Formato de
serie de datos. Canvieu llavors de l'etiqueta Línea l'estil,
el color i el gruix, i de Marcador poseu que no en voleu
cap, així queda ben evident el caràcter continu de la funció de
distribució acumulada teòrica.
- Cliqueu als punts blaus per canviar també el format. Podeu
canviar l'estil i la mida dels punts. Ja hem dit que deixarem d'aquesta
manera la distribució empírica perquè indiqui els punts on hi ha
salt.
- Moveu a mà la mida del gràfic i de l'Área de trazado perquè
es vegi bé el gràfic.
Us suggerim de fer algunes proves noves del test de Kolmogorov-Smirnov
amb les altres variables del full Dades74 del llibre DADES74.XLS
i veureu que per totes s'accepta el model normal.
- Simplement heu de copiar les dades que interessen a la columna A del
full on feu els càlculs del test de Kolomogorov, ordenar-les i llegir-ne
la conclusió.
Podeu veure un exemple en què no s'accepta el model, amb un conjunt de dades
anàlogues a les anteriors, però d'una altra promoció d'alumnes.
- Sense tancar l'altre llibre en el qual treballeu, obriu TERCERJM.XLS.
- Seleccioneu tota la columna D i feu Control + C.
- Obriu (a través de l'opció Ventana) el llibre i el full on
feu el test de Kolmogorov-Smirnov i enganxeu amb Control + V
les dades anteriors a la columna A.
- Elimineu les files de la 102 a la 111 i poseu a C6 que hi ha 100 dades.
- Llegiu la conclusió.
|
 com a prova de normalitat
com a prova de normalitat