| |
|
||||||||||||||||
| Pràctica |
|
Exercicis
|
||||||||||||||
| Els contrastos d'hipòtesis.
La prova khi quadrat |
Glossari
|
|||||||||||||||
|
Proves de normalitat |
||||||||||||||||
| Valoració de la bondat de l'ajust per un model empíric | |
|
En aquesta pràctica es presenta la prova de khi quadrat, que permet valorar la bondat de l'ajust d'unes dades estadístiques (corresponents a una variable alfanumèrica o bé numèrica discreta) a un model de probabilitat. L'objectiu principal és:
|
|
| |
Exemple 1: la primera llei de Mendel |
|
Aquest exemple es comenta a la teoria. Us recomanem que hi accediu per llegir aquests comentaris abans de començar la pràctica. Una investigadora fa encreuaments entre flors blanques i flors vermelles. Cada flor de la primera generació de descendents té genotip BV (un gen de cada progenitor, primera llei de Mendel). Si suposem que cap d'aquests caràcters és dominant sobre l'altre, totes les flors seran roses. Seguidament, continua l'experiment per obtenir la segona generació de descendents i encreua aquestes flors roses. Ens diu que ha obtingut 444 flors, de les quals 102 són blanques, 246 roses i 96 vermelles. Segons les lleis de Mendel (model teòric que volem confrontar), hem d'esperar que les freqüències de flors blanques, roses i vermelles estaran aproximadament en la proporció 1:2:1. D'un total de 444 flors els valors esperats són 111, 222, 111. El test de khi quadrat ens diu si aquests valors estan d'acord amb el model, és a dir, si es pot admetre que la discrepància observada és fruit de l'atzar. El primer que s'ha de fer és introduir els valors observats i els valors esperats en dues columnes d'un full de càlcul.
En aquesta cel·la ha sortit el valor de X2 (consulteu la teoria). Aquest resultat és 5,351351. Podeu fer servir una funció de l'Excel per decidir si les observacions s'ajusten prou bé al model teòric.
Fixeu-vos que el resultat que surt a E6 és 0,068860285. Aquest és l'anomenat valor p de les observacions. Com que aquest valor p és més gran que el nivell de significació (5 % = 0,05), no rebutgem la hipòtesi nul·la i, per tant, podem afirmar que els valors observats estan d'acord amb el model i que les discrepàncies observades són fruit de l'atzar. Com heu vist, la funció =DISTR.CHI(x; graus de llibertat) és molt útil per calcular la probabilitat abans esmentada, entrant el valor calculat prèviament de X2 i fixant els graus de llibertat. Tot i així, l'Excel compta amb una altra funció que encara resol el problema d'una manera més ràpida: és la funció =PRUEBA.CHI(valors observats; valors esperats). Comprovem-ho:
El resultat que surt és el mateix valor p de la cel·la E6, per tant, arribem a les mateixes conclusions d'abans. Si la investigadora s'entestés a dir que vol treballar amb un nivell de significació del 10 %, podeu comprovar que la fórmula =PRUEBA.CHI(A2:A4;B2:B4) permet rebutjar el model, però de seguida la farien reflexionar i li dirien: fes una altra experimentació, perquè un nivell de significació del 10 % és massa agosarat: gairebé mai s'acceptarà el model proposat! En un segon encreuament s'obtenen 320 flors, de les quals 91 són blanques, 144 roses i 85 vermelles. En aquest cas, les freqüències esperades són 80, 160, 80.
Podeu entrar les freqüències observades i esperades respectivament en dues columnes i veureu que en aquest cas, tot i que aparentment també hi ha força discrepància, l'ajust amb el model és molt i molt gran, com indica el valor p de 0,180414 de les cel·les E6 i F6. En aquest cas, se superaria la prova, fins i tot, el nivell de significació del 10 %. |
|
| Exemple 2: són aleatoris els nombres aleatoris de l'Excel? | |
|
En aquest apartat, fareu servir la prova khi quadrat per comprovar si els nombres aleatoris que genera l'Excel són prou aleatoris. Per fer l'experiment, traureu sèries de 120 nombres de l'1 al 6.
Una de les situacions possibles pot ser aquesta: | |
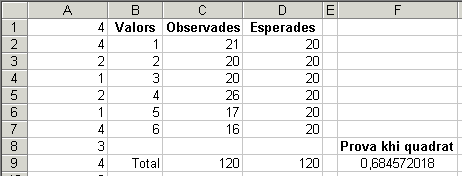 |
|
Penseu que aquesta situació és d'ajust contrastat al model (hem de pensar que els programadors de l'Excel han valorar molt estrictament la generació de nombres aleatoris) i vegeu què passaria segons el nivell de significació amb què treballeu: el 10 % -agosarat, faria rebutjar massa sovint el model- o l'1 % -conservador, el model s'accepta sempre- i entendreu per què el 5 % pot ser un just terme mitjà com a nivell de significació per a les proves estadístiques. Traieu les vostres pròpies conclusions. |
|
| Exemple 3: llançament d'un dau | |
|
Hem fet el recompte de 100 tirades d'un dau i hem observat 9 vegades l'1, 10 vegades el 2, 17 vegades el 3, 20 vegades el 4, 20 vegades el 5 i 24 vegades el 6. Tenim criteris, amb un nivell de significació del 5 %, per pensar que el dau té el pes mal repartit? La hipòtesi nul·la que pensem que hi ha indicis que pot ser rebutjada: dau equilibrat. Les freqüències observades són 9, 10, 17, 20, 20, 24 i les esperades sota la hipòtesi nul·la serien totes iguals; com que hi ha 100 tirades, 100/6 l'1, 100/6 el 2..., que entrarem exactes, no arrodonides, per a una millor aplicació del test. En aquest cas, ja fareu servir directament la funció =PRUEBA.CHI(valors observats; valors esperats).
Observeu el valor p corresponent a les freqüències observades: 0,0564. Si rebutgéssim la hipòtesi dau equilibrat tindríem un risc del 5,64 % d'error (això ens diu el valor p). Conclusió: no tenim criteris suficients (amb el nivell de significació del 5 %) per pensar que el dau està trucat a favor dels números grans; hem de mantenir com a vàlida la hipòtesi de dau equilibrat. Direu segurament: "Per poc, però hem de creure'ns que el dau està equilibrat... de moment! Fem una altra prova!". Hem tornat a tirar 100 vegades el dau i hem observat 10 vegades l'1, 10 vegades el 2, 10 vegades el 3, 10 vegades el 4, 30 vegades el 5 i 30 vegades el 6. Tenim ara criteris, amb un nivell de significació del 5 %, per pensar que el dau té el pes mal repartit?
Aquest nombre tan petit és el poc risc que tenim si rebutgem la hipòtesi que el dau respon al model uniforme. Conclusió: ara sí que podem dir que el dau està trucat! |
|
| Ampliacions, aclariments i comentaris | |
| |
Ampliació
de l'exemple sobre les lleis de Mendel (en concret, sobre la tercera
llei, de l'herència independent dels diversos caràcters).
El vídeo Bondat de l'ajust de la sèrie Estadística i Atzar (BBC, versió de TV3) ens presenta una experiència d'encreuament de flors en què s'estudien dos caràcters de les fulles.
Si ara encreuem aquestes plantes, què succeeix? La tercera llei de Mendel estableix que hi ha independència en la segregació dels gens d'un caràcter i els gens d'un altre. Si això fos cert (i aquesta serà la hipòtesi nul·la del nostre test), totes les possibilitats d'agafar un gen d'un caràcter de cada progenitor i un gen de l'altre caràcter de cada progenitor són igualment probables. Possibilitats: I de l'anàlisi de les 16 possibilitats es dedueix que les freqüències esperades en un encreuament de flors híbrides per tenir la segona generació de descendents han d'estar en la proporció 9:3:3:1. 9/16 és la probabilitat d'obtenir flors de fulles
normal/normal
|
| |
Escrivim la conclusió de la prova de Us proposem que completeu l'exemple de la valoració del model dels nombres aleatoris de l'Excel i així es facilita l'anàlisi de repetides proves que us proposem en el context de la pràctica i, alhora, acabareu d'assolir l'aplicació de la prova de khi quadrat amb un nivell de significació prefixat.
|