Per enviar les respostes als exercicis, elaborareu un document del Word en el qual:

• Posareu un títol per a cada exercici (no cal que hi copieu els enunciats).
• Redactareu, breument, els comentaris adients.
• Inserireu els gràfics que es demanen.

En aquest mòdul heu d'enviar les respostes als tres primers exercicis i a un, si més no, dels opcionals.

• L'exercici 1 enllaça directament amb la pràctica 1; l'exercici 2 amb la pràctica 5 i l'exercici 3 amb la pràctica 4. Aquestes són les tres pràctiques que s'han assenyalat com a fonamentals en les orientacions per al seguiment del mòdul.
• Pel que fa als exercicis opcionals:
  • El quart és un exercici sobre la pràctica 2
  • El cinquè dóna el punt de vista numèric al resultat empíric que permet aproximar la distribució binomial mitjançant la normal.
  • El sisé estudia un model nou de distribució de probabilitat contínua
  • Finalment, el setè és, gaire bé, un tema obert d'investigaciío.

1. Distribució normal.
   Suposeu (encara que no sigui del tot cert) que es pot inferir que les notes de selectivitat de l'alumnat preinscrit a una facultat concreta segueixen un model teòric donat per l'estadística d'anys anteriors, i aquest model és una distribució normal amb una mitjana de 6,4 punts i una desviació estàndard d'1,0 punts.
   1. Quina és la probabilitat que un alumne tregui exactament 7,123456? I que tregui 7,2800000?
   2. Quina és la probabilitat que la nota d'una alumna, arrodonida als centèsims, sigui de 7,28?
   3. Quina és la probabilitat que un alumne tregui més de 7,28? I que la seva nota arrodonida als centèsims sigui més de 7,28?
   4. Quina és la probabilitat que tregui entre 5,70 i 7,50? I que la nota arrodonida als centèsims estigui entre 5,70 i 7,50 (valors inclosos)?
   5. Quina és la nota de tall que cal superar per entrar a l'esmentada facultat si només hi pot entrar el 10 % dels inscrits?
   6. Quines notes delimiten l'interval on queda el 80 % de les notes centrades en la mitjana?
      

2. Comparació de normals
   Representeu, en un mateix gràfic, les funcions de densitat de tres distribucions normals de mitjana 25 i desviacions estàndard 2, 4 i 6, respectivament.
   
   
3. L'enquesta.
   S'ha fet una enquesta a 1.400 persones en una població on el 42 % de les persones eren partidaris del partit ABC.
1. Quina és la probabilitat que en l'enquesta s'obtinguin entre un 39 % i un 45 % favorables a ABC?
2. Quin és l'interval en què, amb una probabilitat del 95 %, quedarà la proporció mostral de persones favorables a A? (Doneu-lo centrat en la mitjana o valor esperat, és a dir, el 42 %, i indiqueu quin seria el marge d'error amb què es dóna la resposta, de manera semblant a allò que s'ha fet en la pràctica 4.)
   
   
4. (Opcional) Partícules radioactives.
   La vida mitjana d'unes partícules radioactives molt poc estables és de 22 segons.
1. Quina proporció de matèria d'aquestes característiques podem pensar que romandrà al cap de 22 segons? (Penseu que 22 segons és la mitjana.) I al cap de 25 segons?
2. Quant de temps ha de passar perquè només quedi la meitat de la matèria radioactiva? I perquè perdi el 75 % del total?



5. (Opcional) Aproximació de la binomial per la normal.
   Jutgeu numèricament la bondat de l'ajustament de la distribució binomial mitjançant la normal. A les pràctiques 3 i 4 d'aquest mòdul heu estudiat casos d'aproximació de la binomial mitjançant la normal i s'ha formulat estrictament quins són els valors que cal considerar.

   1. Calculeu el valor de p(X = 12) en la binomial B(40, 0,25); calculeu, també, el valor de p[11,5 X_n 12,5] en la distribució normal N(10, 2,739) i el valor de f(12) en la funció de densitat de probabilitat associada a aquesta normal. Comenteu els valors observats.
   2. Compareu ara els valors de p[X=18] en la distribució binomial de n = 60, p = 0,3 amb el valor que s'obté si es calcula la p[17,5 < X_n< 18,5] en la corresponent distribució normal i amb el valor de f(18) si és f la funció de densitat d'aquesta distribució normal.
   3. Finalment, compareu els valors numèrics que dóna l'ordinador per a p[X=45], en la distribució binomial de n = 100, p = 0,45 amb el valor que s'obté si es calcula la p[44,5 < X_n< 45,5] corresponent a la distribució normal associada, que és la que té mitjana n · p = 45 i desviació estàndard 4,975. Calculeu, també, com en els apartats anteriors, f(45).
      

6. (Opcional) La línia d'autobusos.
   En l'exposició de la distribució uniforme hem presentat un exemple que ara variarem lleugerament. En una línia d'autobusos, aquests passen exactament cada 10 minuts. Una persona que els fa servir sovint procura anar-hi sempre més o menys a la meitat de l'interval entre pas i pas. Tanmateix, les circumstàncies fan que tant es pugui retardar una mica com avançar, però amb la idea prioritària ja indicada.
   1. Un amic seu li diu que el model de probabilitat que regula l'estona que haurà d'esperar l'autobús té una funció de densitat amb aquesta gràfica:
      
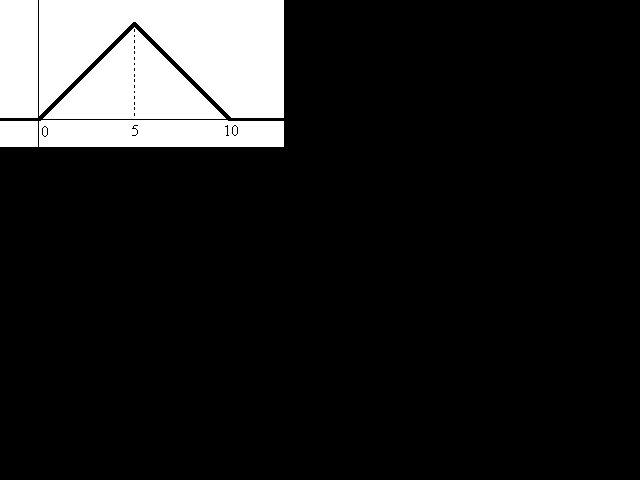
      Sabent que l'àrea total sota la funció de densitat és 1, calculeu l'altura del triangle i, per raonaments geomètrics, calculeu també la probabilitat que s'hagi d'esperar entre 4 i 6 minuts.
   2. Una amiga, estudiant d'estadística, li diu, en canvi, que el temps d'espera segurament estarà modelitzat per una distribució normal de mitjana 5 minuts i desviació estàndard 1,5 minuts. Si fos realment així, quina seria la probabilitat d'esperar-se entre 4 i 6 minuts?
      
      

7. (Opcional) Exemples diversos.
   Digueu, raonadament (amb raonaments gràfics o numèrics i confrontant si cal dades empíriques amb valors de probabilitat), quina o quines de les situacions següents us sembla que poden ser modelitzades per una distribució exponencial i, en cas contrari, proposeu un model.
   1. El minut en què es marca el primer gol en un partit de futbol.
   2. La durada d'unes piles elèctriques de les quals ens han donat la taula següent, referida a 500 unitats:

      Durada en hores	Freqüència
      0 - 50 50 - 100 100 - 150 150 - 200 200 - 250 250 - 300 300 - 350 350 - 400	208 112 75 40 30 18 11 6

       
      
   3. La durada dels pneumàtics de cotxe d'una determinada marca.